Spectral Graph Clustering under Differential Privacy: Balancing Privacy, Accuracy, and Efficiency

Abstract: We study the problem of spectral graph clustering under edge differential privacy (DP). Specifically, we develop three mechanisms: (i) graph perturbation via randomized edge flipping combined with adjacency matrix shuffling, which enforces edge privacy while preserving key spectral properties of the graph. Importantly, shuffling considerably amplifies the guarantees: whereas flipping edges with a fixed probability alone provides only a constant epsilon edge DP guarantee as the number of nodes grows, the shuffled mechanism achieves (epsilon, delta) edge DP with parameters that tend to zero as the number of nodes increase; (ii) private graph projection with additive Gaussian noise in a lower-dimensional space to reduce dimensionality and computational complexity; and (iii) a noisy power iteration method that distributes Gaussian noise across iterations to ensure edge DP while maintaining convergence. Our analysis provides rigorous privacy guarantees and a precise characterization of the misclassification error rate. Experiments on synthetic and real-world networks validate our theoretical analysis and illustrate the practical privacy-utility trade-offs.

• The paper presents three novel mechanisms—matrix shuffling, projected Gaussian, and noisy power method—to balance privacy and accuracy in spectral graph clustering.
• It rigorously analyzes each method's privacy guarantees and misclassification error bounds using both theoretical derivations and experimental validations.
• Empirical results on synthetic and real-world datasets demonstrate the practical trade-offs between computational efficiency and robust edge differential privacy.

Spectral Graph Clustering under Differential Privacy: Balancing Privacy, Accuracy, and Efficiency

Introduction

The paper "Spectral Graph Clustering under Differential Privacy: Balancing Privacy, Accuracy, and Efficiency" addresses the challenges of performing spectral graph clustering while ensuring edge differential privacy (DP). The authors propose three different mechanisms that provide varying degrees of privacy, accuracy, and computational efficiency. These are (i) graph perturbation with randomized edge flipping and adjacency matrix shuffling, (ii) private graph projection with Gaussian noise, and (iii) a noisy power method. Each mechanism is analyzed in terms of its privacy guarantees and clustering accuracy, with experiments validating the theoretical findings on both synthetic and real-world datasets.

Mechanisms for Privacy-Preserving Spectral Clustering

The paper introduces three novel mechanisms, each balancing privacy and utility differently:

1. Matrix Shuffling Mechanism: This method involves perturbing the graph by flipping edges with a fixed probability and then shuffling the adjacency matrix. The shuffling amplifies the privacy guarantees, achieving $(\varepsilon, \delta)$-edge DP with decreasing parameters as the number of nodes increases. This approach provides the best error rate at the expense of higher computational complexity.

Figure 1: Synopsis of results for the three different mechanisms: error rate vs.\ $\varepsilon$.

2. Projected Gaussian Mechanism: This mechanism performs dimensionality reduction via random projections followed by Gaussian noise addition. It allows for efficient computation by reducing both time and space complexity, achieving favorable trade-offs for large graphs.

Figure 2: Left: Eigenvalues of the perturbed and adjacency matrix that is similarity transformed with random permutation similarity transformation. Right: the $(\delta)$-DP guarantees of the perturbed and shuffled result, when the perturbed only result is $\varepsilon_0$-DP for $\varepsilon_0=2.2.$

3. Noisy Power Method Mechanism: By injecting noise in a power iteration method, this mechanism ensures convergence while maintaining privacy. It offers a balanced approach particularly effective for dense graphs, promising improved scalability with the number of iterations and noise variance.

Theoretical Analysis

The paper provides rigorous proofs of the privacy guarantees for each mechanism and derives misclassification error bounds. It establishes that the matrix shuffling method achieves the lowest error rate due to the strong amplification effect. The projected Gaussian mechanism reduces space complexity significantly, suitable for use when the reduced dimension is much smaller than the number of nodes. On the other hand, the noisy power method offers a compromise between accuracy and efficiency, especially suitable for scenarios with a large number of graph nodes.

Experimental Validation

Experiments on both synthetic and real-world graphs demonstrate the efficacy of the proposed methods. Results show that the graph perturbation method with shuffling provides the best privacy-utility trade-off, achieving high clustering accuracy with robust privacy guarantees. Meanwhile, the other methods offer computational efficiency, making them practical for larger datasets.

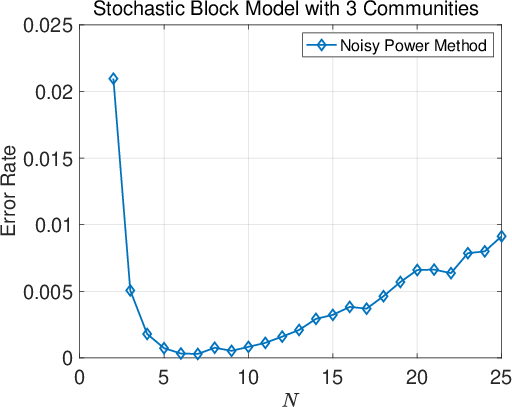
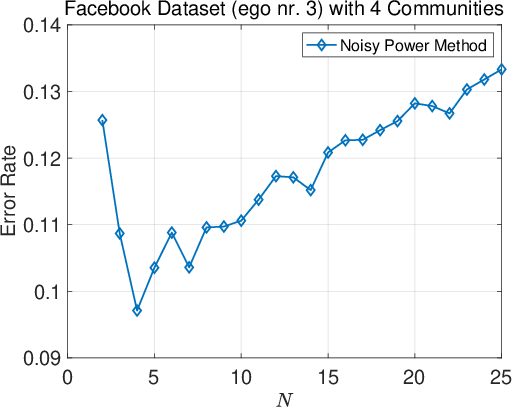
Figure 3: Ablation on the number of iterations $N$ in the noisy power method across all four datasets.

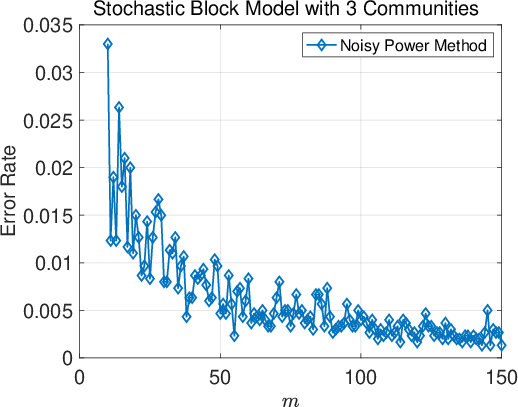
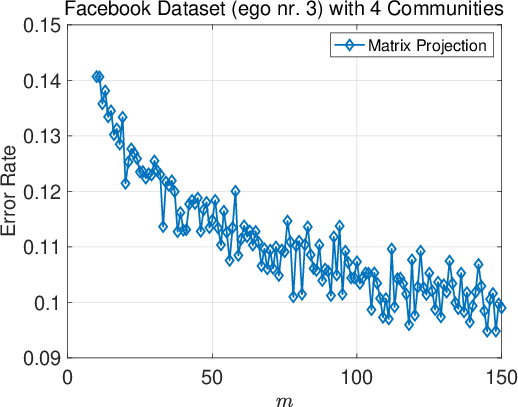
Figure 4: Ablation on the projection dimension $m$ for the matrix projection method. Results are reported for the two datasets where the mechanism is effective.

Conclusion

In conclusion, the paper contributes significantly to privacy-preserving graph analysis by proposing three distinct mechanisms that balance privacy and utility in spectral clustering. The results emphasize the importance of considering computational efficiency alongside privacy guarantees. Future work could explore extensions to attributed graphs, offering new challenges in maintaining node privacy with complex data attributes. The findings pave the way for more robust applications of differential privacy in large-scale network analysis, further enhancing the capability of analyzing sensitive data while respecting privacy constraints.