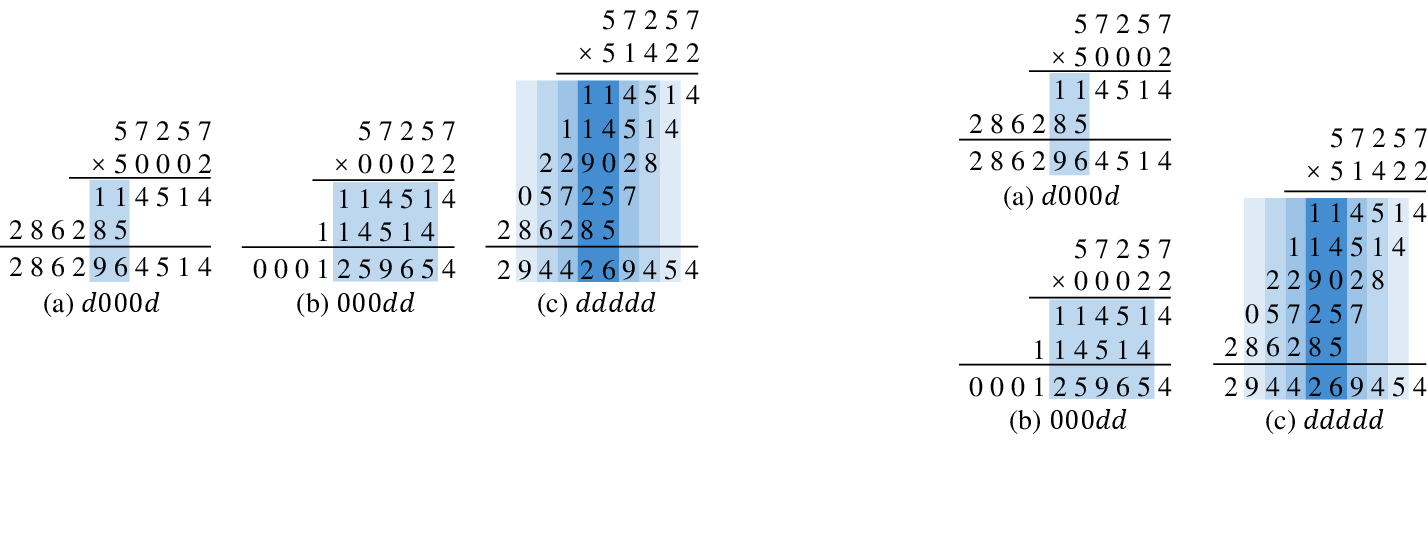Dissecting Multiplication in Transformers: Insights into LLMs (2407.15360v1)

Abstract: Transformer-based LLMs have achieved remarkable performance across various natural language processing tasks. However, they often struggle with seemingly easy tasks like arithmetic despite their vast capabilities. This stark disparity raise human's concerns about their safe and ethical use, hinder their widespread adoption.In this paper, we focus on a typical arithmetic task, integer multiplication, to explore and explain the imperfection of transformers in this domain. We provide comprehensive analysis of a vanilla transformer trained to perform n-digit integer multiplication. Our observations indicate that the model decomposes multiplication task into multiple parallel subtasks, sequentially optimizing each subtask for each digit to complete the final multiplication. Based on observation and analysis, we infer the reasons of transformers deficiencies in multiplication tasks lies in their difficulty in calculating successive carryovers and caching intermediate results, and confirmed this inference through experiments. Guided by these findings, we propose improvements to enhance transformers performance on multiplication tasks. These enhancements are validated through rigorous testing and mathematical modeling, not only enhance transformer's interpretability, but also improve its performance, e.g., we achieve over 99.9% accuracy on 5-digit integer multiplication with a tiny transformer, outperform LLMs GPT-4. Our method contributes to the broader fields of model understanding and interpretability, paving the way for analyzing more complex tasks and Transformer models. This work underscores the importance of explainable AI, helping to build trust in LLMs and promoting their adoption in critical applications.

• The paper identifies transformers' primary shortcoming in handling carry propagation and overlapping products in multi-digit multiplication.
• The methodology dissects multiplication into subtasks and analyzes per-digit loss curves to trace the sequential learning path.
• Enhancements such as reversing answer digits, deepening model architecture, and refining training data achieved 99.9% accuracy on 5-digit multiplications.

Dissecting Multiplication in Transformers: Insights into LLMs

This paper explores the mechanics of how transformer-based LLMs, despite their expansive capabilities, struggle with basic arithmetic tasks such as integer multiplication. The paper provides a detailed exploration of transformers trained on $n$-digit integer multiplication tasks and uncovers the intrinsic architectural and operational shortcomings that lead to these deficiencies.

Insights into Transformer Shortcomings

Transformers decompose arithmetic tasks, particularly multiplication, into several parallel subtasks such as Base Multiply, Carry, and Use Carry. This decomposition occurs across individual digits sequentially and constitutes the primary framework through which transformers endeavor to solve multiplication problems. Notably, transformers encounter considerable difficulty with successive carryovers and caching intermediate results, which are crucial for accurately solving multi-digit multiplication.

Figure 1: The decomposed steps of (a) addition, (b) multi-digit and unit-digit ($m\times u$) multiplication, and (c) multi-digit and multi-digit ($m\times m$) multiplication.

Per-digit Loss Analysis

Through analyzing the per-digit loss curves, the paper observes a sequential learning path where simpler tasks are learned first before more complex operations are addressed. The units digit A0 and the terminal digit A5 are mastered swiftly due to their simplified requirements compared to intermediate digits that depend on cumulative carry calculations.

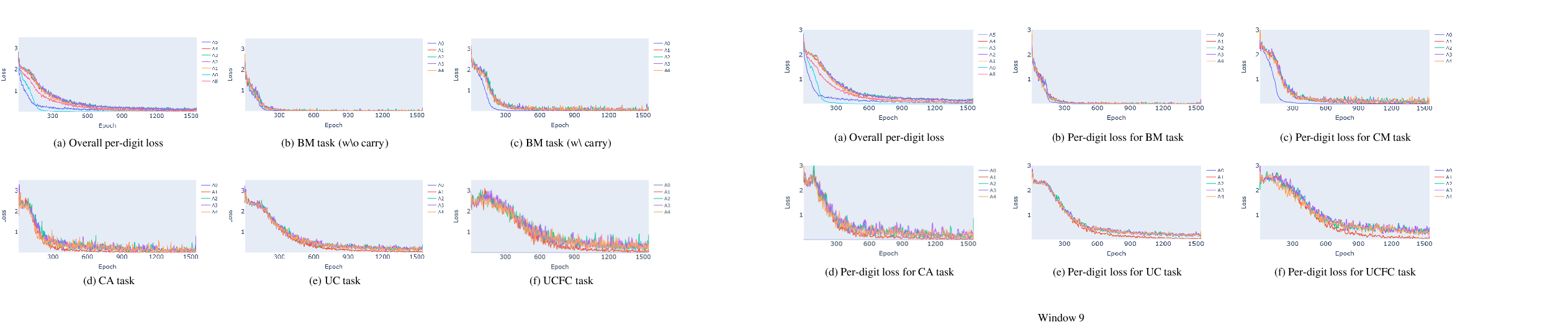
Figure 2: Illustrations of (a) the overall per-digit loss curve, and (b-f) per-digit loss curve for each subtask.

Attention Mechanism Behavior

The investigation into the attention maps reveals that specific heads are designated to distinct subtasks in the multiplication sequence. In reversed answer digit formats, where calculations start from lower-order digits, transformers manifest superiority in performance because they can utilize previously generated digits, enhancing overall accuracy.

Figure 3: Attention map of ordinal and reversed answer digit format. To predict answer digit, the multiple attention heads are responsible for different tasks and combine the information in subsequent MLP layers.

Multiplier Format and Tasks Overlap

Performance deteriorates when multiple products overlap within intermediate multi-digit results, suggesting that transformers have limited capacity to handle extensive overlapping products, which is common in complex multi-digit multiplications.

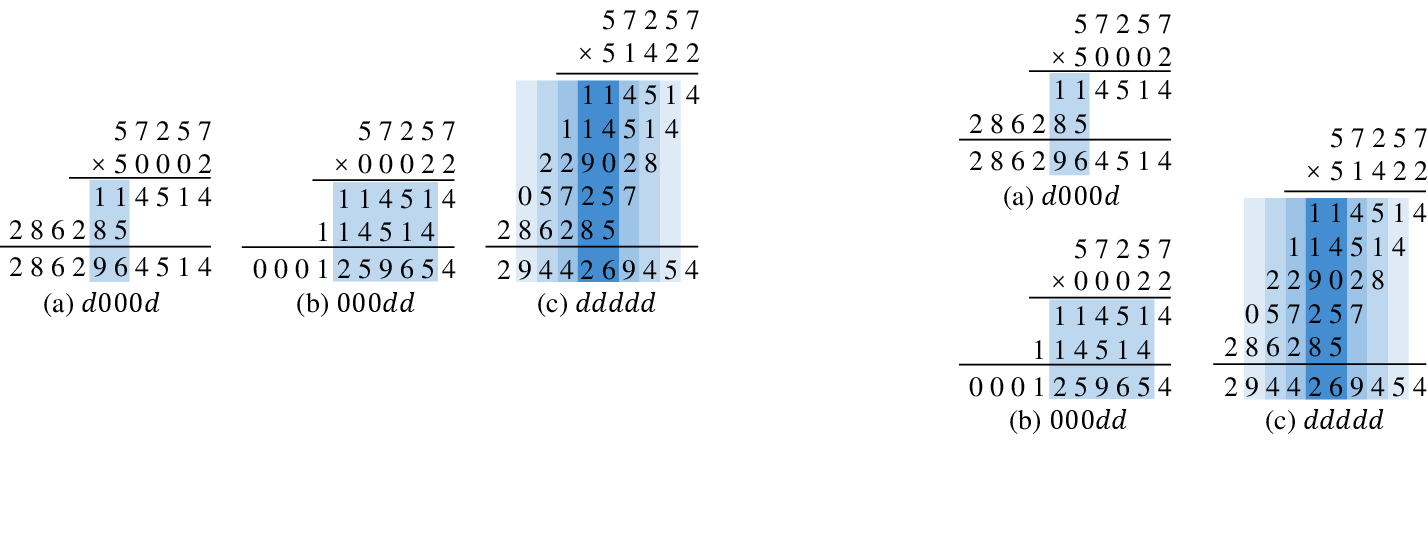
Figure 4: The overlap of per-digit product with different multiplier format. The darker the color, the more overlapping digits there are.

Proposed Enhancements and Results

To enhance transformer performance in arithmetic tasks, the paper proposes several refinements: reversing answer digits, increasing model depth, and adjusting the training dataset to have a higher proportion of simple samples. By implementing these strategies, transformers achieve 99.9% accuracy on 5-digit integer multiplications, even outperforming existing sophisticated models like GPT-4 in these specific tasks.

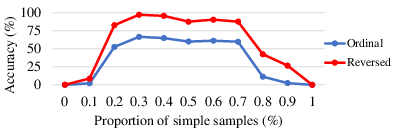
Figure 5: Accuracy (\%) of ordinal and reversed transformer trained with different proportion of simple samples.

Conclusion

The paper successfully identifies critical architectural limitations affecting transformer performance on arithmetic tasks and proposes effective solutions, focusing on enhancing model capacity and optimizing training datasets. These findings not only bolster arithmetic task proficiency but also pave the path for further investigations into transformer applications in more complex tasks. The contributions emphasize the necessity for explainable AI to augment trust in LLMs, particularly in scenarios requiring high reliability and safety.