FMamba: Mamba based on Fast-attention for Multivariate Time-series Forecasting (2407.14814v1)

Abstract: In multivariate time-series forecasting (MTSF), extracting the temporal correlations of the input sequences is crucial. While popular Transformer-based predictive models can perform well, their quadratic computational complexity results in inefficiency and high overhead. The recently emerged Mamba, a selective state space model, has shown promising results in many fields due to its strong temporal feature extraction capabilities and linear computational complexity. However, due to the unilateral nature of Mamba, channel-independent predictive models based on Mamba cannot attend to the relationships among all variables in the manner of Transformer-based models. To address this issue, we combine fast-attention with Mamba to introduce a novel framework named FMamba for MTSF. Technically, we first extract the temporal features of the input variables through an embedding layer, then compute the dependencies among input variables via the fast-attention module. Subsequently, we use Mamba to selectively deal with the input features and further extract the temporal dependencies of the variables through the multi-layer perceptron block (MLP-block). Finally, FMamba obtains the predictive results through the projector, a linear layer. Experimental results on eight public datasets demonstrate that FMamba can achieve state-of-the-art performance while maintaining low computational overhead.

• The paper introduces FMamba, a framework combining fast-attention and Mamba for efficient multivariate time-series forecasting.
• It employs a Gaussian kernel in fast-attention to capture inter-variable correlations while reducing computational overhead.
• Experimental results show significant improvements in MSE and MAE over SOTA models on eight public datasets.

FMamba: Mamba Based on Fast-Attention for Multivariate Time-Series Forecasting

This paper introduces FMamba, a novel framework for MTSF that combines fast-attention with Mamba to address the limitations of existing Transformer-based models and channel-independent predictive models based on Mamba (2407.14814). The authors aim to capture both inter-variable correlations and intra-series temporal dependencies efficiently. FMamba leverages the strengths of both fast-attention and Mamba, achieving SOTA performance on eight public datasets while maintaining linear computational complexity.

FMamba Architecture and Implementation

FMamba's architecture (Figure 1) comprises an Embedding layer, fast-attention mechanism, Mamba module, and a linear projector.

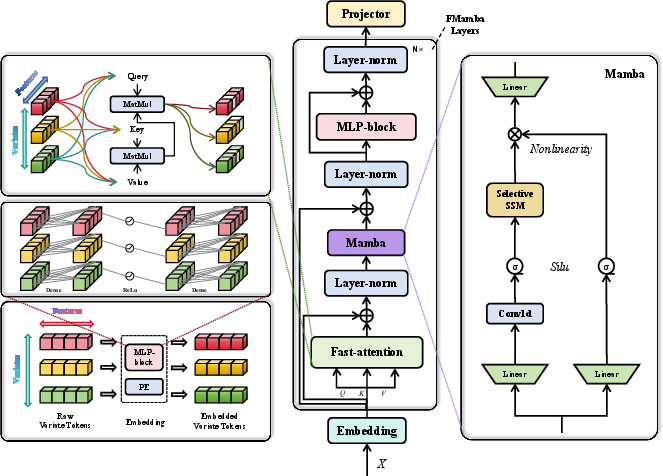
Figure 1: The structure of FMamba.

The Embedding layer extracts initial temporal features using positional encoding and MLP-blocks. The fast-attention mechanism (Figure 2) then captures dependencies among input variables with linear computational complexity, addressing the quadratic complexity of traditional self-attention.

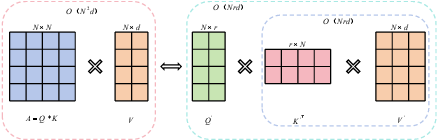
Figure 2: The illustration of canonical self-attention and fast-attention.

Mamba selectively processes input features, focusing on relevant information between variables, while the MLP-block extracts deeper temporal information. Finally, the projector generates the forecasting results.

The fast-attention mechanism employs a Gaussian kernel function $\mathcal{F}$ to transform the input non-linearly:

$\mathcal{F}(x) = exp (\frac{-x^2}{2})$

The attention is then computed as:

$\text{Attention}(\mathbf{Q'}, \mathbf{K'}, \mathbf{V'}) = \frac{\mathbf{Q'}{k\_{dim} \left(\mathbf{K'}^\top \mathbf{V'}\right)$

where $\mathbf{Q'}$, $\mathbf{K'}$, and $\mathbf{V'}$ are the transformed query, key, and value matrices, respectively, and $k\_{dim}$ denotes the kernel dimension.

The Mamba module is based on SSM, which can be described by the equations:

$$\begin{aligned} h(t)^{\prime} & =\boldsymbol{A} h(t)+\boldsymbol{B} x(t) ,\ y(t) & =\boldsymbol{C} h(t), \end{aligned}$$

where $h(t)$ is the latent state, $x(t)$ is the input, $y(t)$ is the output, and $\boldsymbol{A}$, $\boldsymbol{B}$, and $\boldsymbol{C}$ are learnable parameter matrices. Mamba parameterizes the input of SSM to enable selective processing of input sequences. The Mamba Block's process is detailed in Algorithm 1 of the paper.

Experimental Evaluation

The authors conducted experiments on eight public datasets, including PEMS03, PEMS04, PEMS07, PEMS08, Electricity, SML2010, Weather, and Solar-Energy. The performance of FMamba was compared against 11 SOTA models, including S-Mamba, iTransformer, RLinear, PatchTST, Crossformer, TiDE, TimesNet, DLinear, SCINet, FEDformer, and Stationary. The evaluation metrics used were MSE and MAE.

The results (Table 2 of the paper) demonstrate that FMamba achieves SOTA performance on most datasets, with lower MSE and MAE compared to the baselines. For instance, FMamba shows an improvement in average MSE compared to S-Mamba on PEMS03 (22.8%), PEMS08 (26.3%), and Solar-Energy (12.7%). Compared to iTransformer, FMamba also shows an overall improvement in average MSE across all datasets, such as 21.8% in PEMS07 and 23.3% in PEMS08.

Visualizations of the forecasting results (Figure 3 and Figure 4) further illustrate the effectiveness of FMamba in capturing the underlying patterns in the time-series data.

Figure 3: Comparison of forecasting between FMamba and S-Mamba on PEMS03 and Weather when the input length is 96 and the forecasting length is 96.

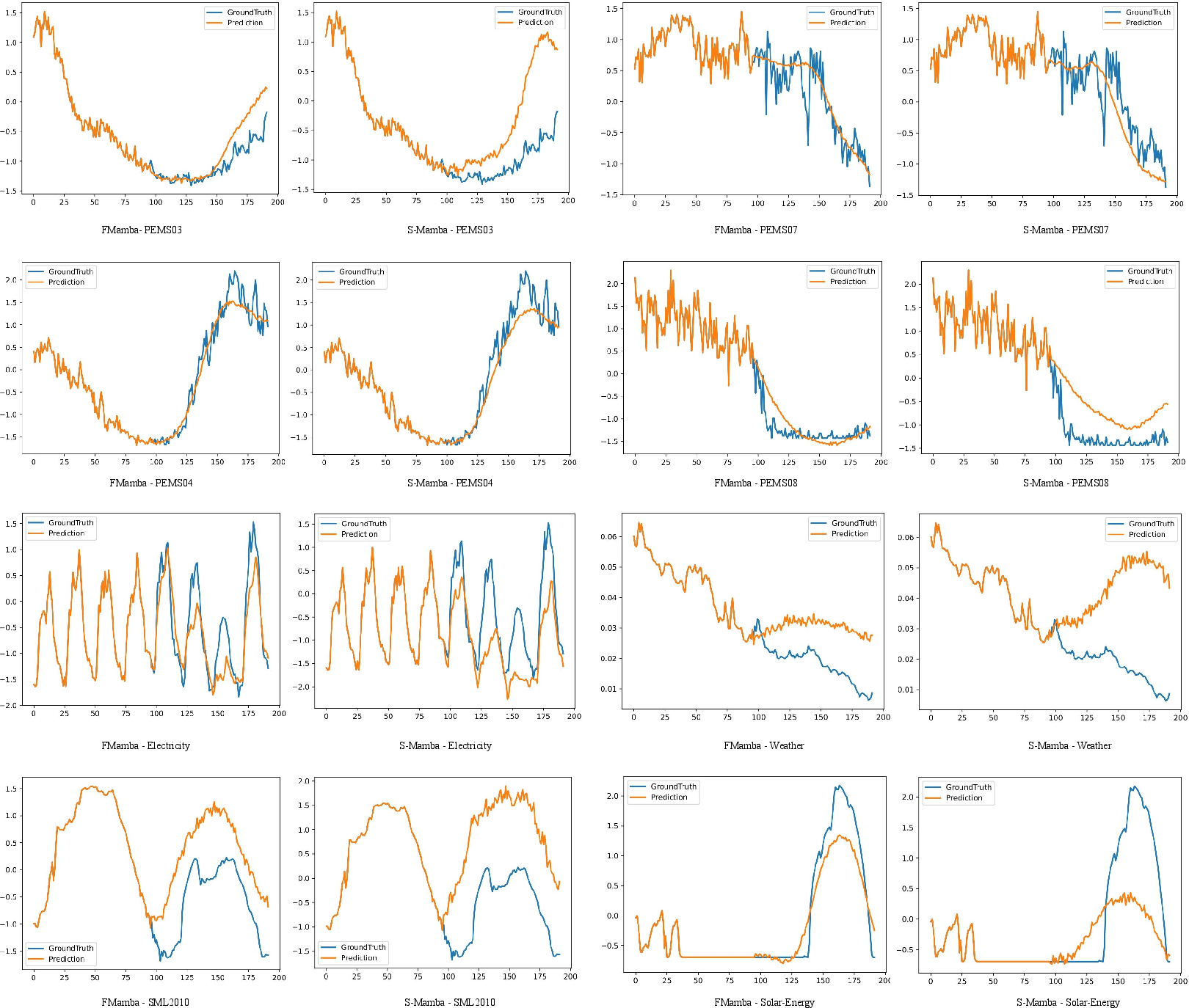
Figure 4: Comparison of forecasts between FMamba and S-Mamba on eight datasets when the input length is 96 and the forecast length is 96. The blue line represents the ground truth and the orange line represents the forecast.

Ablation studies validate the contribution of each component in FMamba. Replacing fast-attention with self-attention has little impact, suggesting that fast-attention can achieve comparable performance with reduced computational overhead. Replacing Mamba with self-attention significantly impacts the model's performance, indicating that Mamba's selective processing enhances the model's robustness.

Parameter sensitivity analysis (Figure 5) shows that FMamba is robust to variations in input length, learning rate, kernel dimension, and state dimension.

Figure 5: The parameter sensitivity of four components in FMamba.

Conclusion

The FMamba framework offers a promising approach for MTSF, combining the strengths of fast-attention and Mamba to achieve SOTA performance with linear computational complexity. The model's architecture and experimental results demonstrate its effectiveness in capturing both inter-variable correlations and intra-series temporal dependencies. Future work could explore further optimizations of the FMamba architecture and its application to other time-series forecasting tasks.