Human-like Episodic Memory for Infinite Context LLMs (2407.09450v2)

Abstract: LLMs have shown remarkable capabilities, but still struggle with processing extensive contexts, limiting their ability to maintain coherence and accuracy over long sequences. In contrast, the human brain excels at organising and retrieving episodic experiences across vast temporal scales, spanning a lifetime. In this work, we introduce EM-LLM, a novel approach that integrates key aspects of human episodic memory and event cognition into LLMs with no fine-tuning, enabling them to handle practically infinite context lengths while maintaining computational efficiency. EM-LLM organises sequences of tokens into coherent episodic events using a combination of Bayesian surprise and graph-theoretic boundary refinement in an online fashion. When needed, these events are retrieved through a two-stage memory process, combining similarity-based and temporally contiguous retrieval for efficient and human-like access to relevant information. Experiments on the LongBench and InfiniteBench benchmarks demonstrate EM-LLM's superior performance, consistently outperforming the state-of-the-art retrieval model InfLLM across various baseline LLMs. In addition, EM-LLM outperforms its popular counterpart, RAG, in a wide range of tasks, while requiring similar resources. Notably, EM-LLM's performance even surpasses full-context models in most tasks, while successfully performing retrieval across 10 million tokens - a scale computationally infeasible for such models. Finally, our analysis reveals strong correlations between EM-LLM's event segmentation and human-perceived events, suggesting a bridge between this artificial system and its biological counterpart, thereby offering a novel computational framework for exploring human memory mechanisms.

• The paper introduces EM-LLM, a novel architecture that incorporates human-like episodic memory using surprise-based segmentation to manage infinite context.
• It employs graph-theoretic metrics to refine event boundaries, enhancing cohesion and information retrieval efficiency within segmented memory units.
• Experimental results demonstrate a 4.3% overall improvement and a 33% enhancement in passage retrieval, validating its performance over existing models.

EM-LLM: Integrating Episodic Memory into LLMs

The paper "Human-like Episodic Memory for Infinite Context LLMs" (2407.09450) introduces EM-LLM, a novel architecture designed to enhance the ability of LLMs to process extensive contexts by incorporating principles of human episodic memory. This approach addresses the limitations of traditional Transformer-based LLMs in handling long sequences, offering a scalable solution for managing virtually infinite context windows. By segmenting input sequences into episodic events based on surprise and refining these boundaries using graph-theoretic metrics, EM-LLM aims to improve both the efficiency and relevance of information retrieval in LLMs.

Background and Motivation

The context window limitations of LLMs pose a significant challenge for maintaining coherence and accuracy over long sequences. While techniques like retrieval-augmented generation (RAG) and key-value pair retrieval have shown promise, a performance gap persists between short- and long-context tasks. The human brain, in contrast, excels at organizing and retrieving episodic experiences across vast temporal scales. Drawing inspiration from this, EM-LLM integrates key aspects of event cognition and episodic memory into LLMs.

The human brain segments continuous experience into discrete episodic events, organized hierarchically and stored in long-term memory. Event boundaries are crucial access points for memory retrieval and often correspond to moments of high prediction error, or "surprise." EM-LLM leverages these insights to dynamically segment token sequences based on the model's surprise during inference, refining these boundaries to maximize cohesion within memory units and separation between them.

EM-LLM Architecture and Mechanisms

EM-LLM is designed to be applied directly to pre-trained LLMs, enabling them to handle context lengths significantly larger than their original training length. The architecture divides the context into initial tokens, evicted tokens managed by the proposed memory model, and a local context utilizing full softmax attention to maximize information about the current task. This structure mirrors cognitive models of working memory.

Memory Formation via Surprise

The memory formation process begins by segmenting the sequence of tokens into individual memory units representing episodic events. Boundaries are initially determined dynamically based on the model's surprise during inference, quantified by the negative log-likelihood of observing the current token given previous tokens. A token $x_t$ is considered a potential boundary if its surprise value exceeds a threshold $T$:

$$-\log P(x_t|x_1,\ldots,x_{t-1};\theta) > T \quad \text{with} \quad T = \mu_{t-\tau} + \gamma\sigma_{t-\tau}$$

where $\mu_{t-\tau:t}$ and $\sigma_{t-\tau:t}^2$ are the mean and variance of surprise for a window offset $\tau$, and $\gamma$ is a scaling factor.

Boundary Refinement

The initial surprise-based boundaries are then refined to maximize cohesion within memory units and separation of memory content across them. This refinement process leverages graph-theoretic metrics, treating the similarity between attention keys as a weighted adjacency matrix. The adjacency matrix $A^h$ is defined as:

$A^h_{ij}=\text{sim}(K^h_i,K^h_j),$

where $K^h_i$ and $K^h_j$ are the key vectors corresponding to tokens $x_i$ and $x_j$, respectively, and the similarity function measures the closeness of two key vectors.

Figure 1: Group-based $k$-NN retrieval can be seen as a form of hierarchical episodic attention. Initially, $k=4$ groups of tokens are selected (left) and then used for softmax attention (right), as if all other similarity scores were forced to be zero (non-shaded areas of the left curve). This framework can support multiple levels of episodic attention.

The algorithm iteratively adjusts the initial surprise-based boundaries to optimize metrics such as modularity and conductance, which quantify the cohesion within events and separation between events based on the graph structure. Modularity is defined as:

$f_M(A^h,\mathcal{B}) = \frac{1}{4m} \sum_{i,j} \left[A^h_{ij} - \frac{\sum_{i}A^h_{ij} \cdot \sum_{j}A^h_{ij}{2m}\right] \delta(c_i, c_j)$

where $m$ is the total edge weight in the graph, $c_i$ is the community (episodic event) to which node $i$ is assigned, and $\delta$ is the Kronecker delta function.

Conductance, on the other hand, is defined as:

$$f_C(A^h,\mathcal{B}) = \min_{S\in V}\frac{\sum_{i \in S,j \notin S} A^h_{ij}}{\min(\text{vol}(S), \text{vol}(V \setminus S))},\qquad \text{with}\; \text{vol}(S) = \sum_{i\in S,j\in S}A_{ij},\; \text{vol}(V\setminus S) = \sum_{i\notin S,j\notin S}A_{ij}$$

where $S = \{b_i,b_i+1,...,b_{i+1}\}$ is a subset of all nodes $V = \{b_1,b_1+1,...,b_k\}$ in the induced graph, with $b_i \in \mathcal{B}$.

Memory Retrieval

The memory retrieval process employs a two-stage mechanism. First, $k_s$ events are retrieved using $k$-NN search based on dot product similarity between the current query and representative tokens of each event, forming a similarity buffer. Second, a contiguity buffer of size $k_c$ maintains temporal context by enqueuing neighboring events, promoting temporal relationships in retrieval.

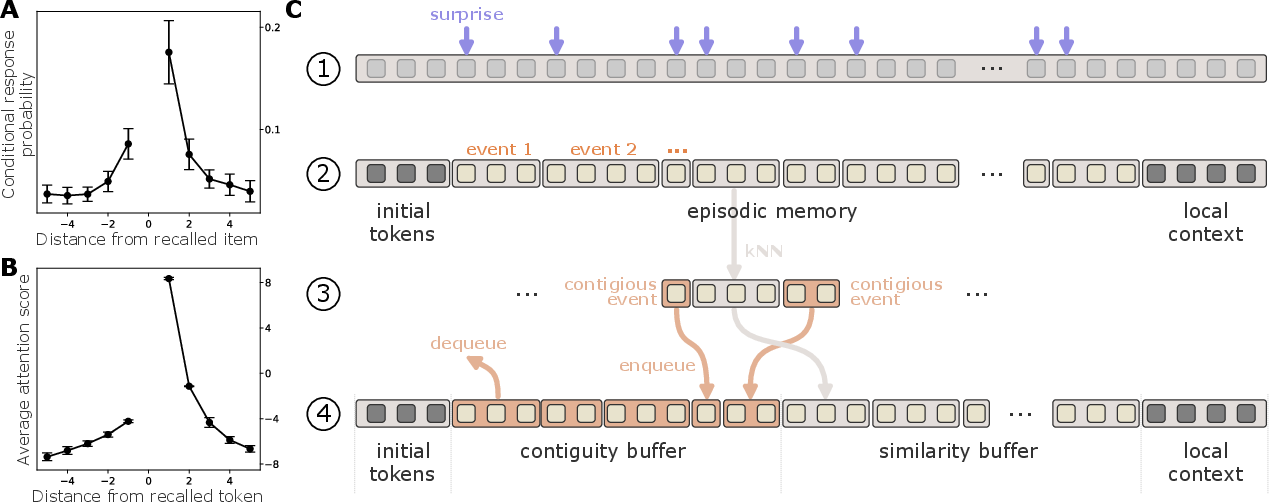
Figure 2: (A) Example of the temporal contiguity and asymmetry effect in human free recall. Data averaged over several large free recall studies (adopted from \citealp{Howard:2002:TCM}).

Experimental Results

The effectiveness of EM-LLM was evaluated on the LongBench dataset, demonstrating superior performance compared to the state-of-the-art InfLLM model [xiao2024infllm]. EM-LLM achieved an overall relative improvement of $4.3\%$, including a $33\%$ improvement on the PassageRetrieval task, which requires accurate recall of detailed information from a large context.

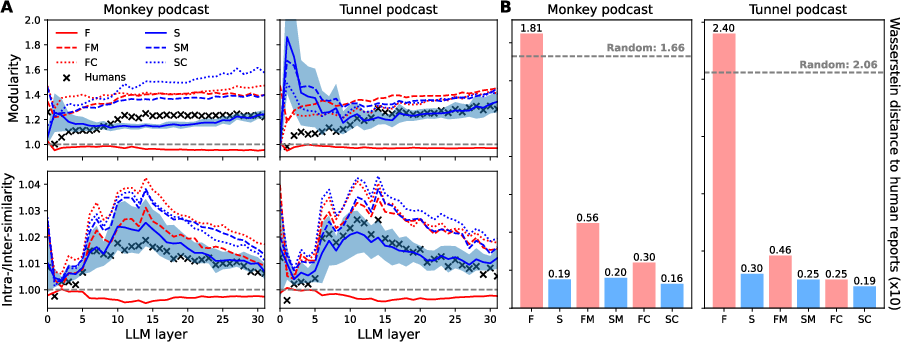
Figure 3: Comparison of human event segmentation with different computational segmentation methods in two human-annotated audio datasets (see Appendix~\ref{appdx:human_data).

Ablation studies (Figure 4 and Figure 5) further highlighted the contributions of surprise-based segmentation, boundary refinement, and the contiguity buffer. Additionally, analysis using human-annotated podcast scripts showed strong correlations between EM-LLM's event segmentation and human-perceived events, suggesting that LLM-perceived surprise can serve as a proxy for the cognitive signals that drive human event segmentation.

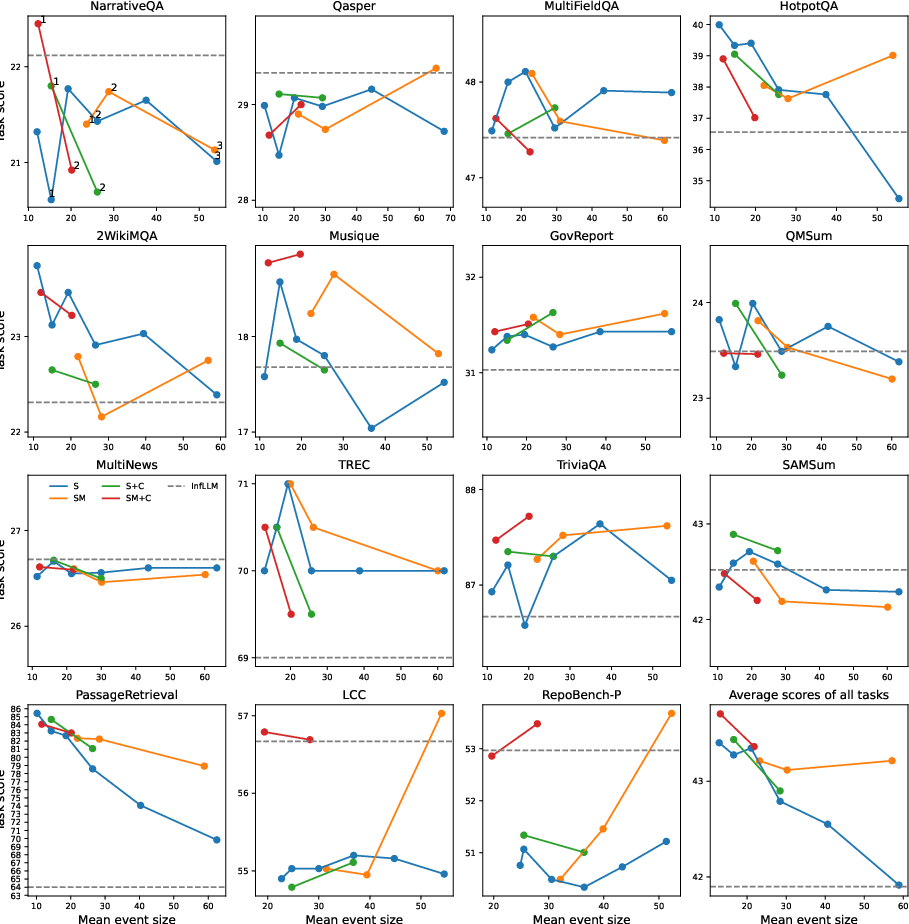
Figure 4: Ablation paper in LongBench. Comparison of EM-LLM performance for different combinations of model features (represented by different colours) and different values of gamma (the threshold's scaling factor). Model variants are aligned on the x-axis based on the average number of block size that emerges for each case. The gamma values for each model variant are shown in the first sub-plot. The corresponding InfLLM performance is also shown.

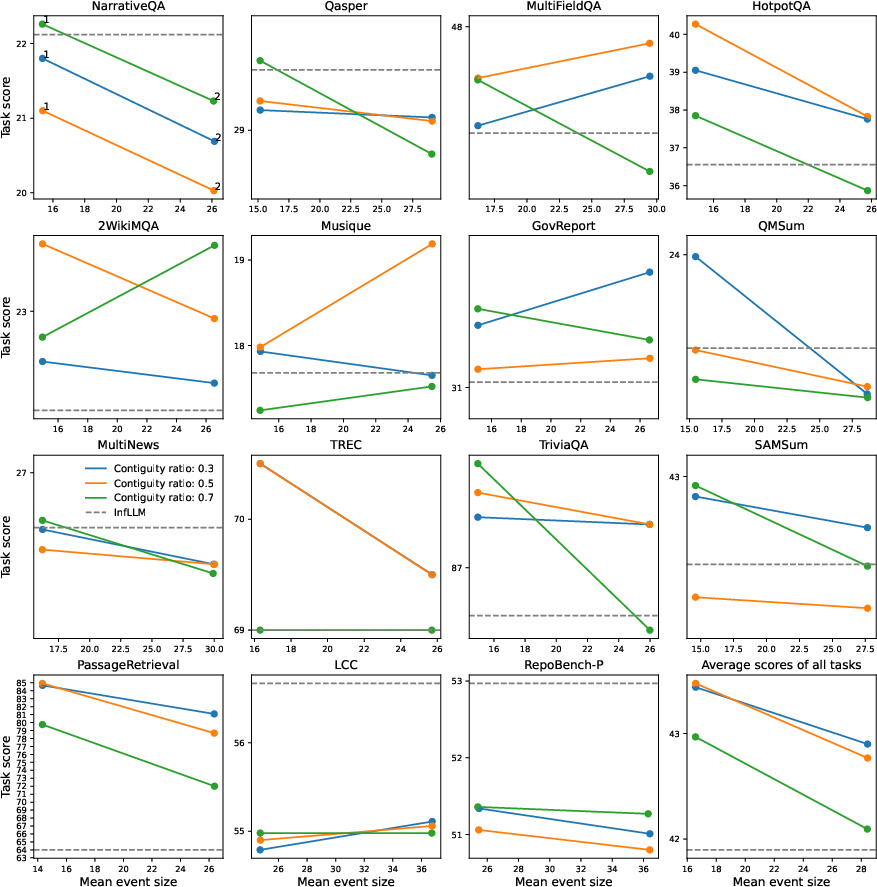
Figure 5: Ablation paper in LongBench. Comparison of EM-LLM performance for different ratios of the contiguity and similarity buffers (represented by different colours) and different values of gamma. Model variants are aligned on the x-axis based on the average number of block size that emerges for each case. The gamma values for each model variant are shown in the first sub-plot. The corresponding InfLLM performance is also shown.

Discussion and Implications

The surprise-based segmentation and boundary refinement processes in EM-LLM mirror key aspects of human event perception and memory formation. The approach aligns with theories proposing that humans segment continuous experiences into discrete events based on prediction errors or moments of surprise. Furthermore, the model's use of both similarity-based and temporally contiguous retrieval mechanisms parallels human memory retrieval patterns.

The architecture of EM-LLM also invites interesting comparisons to cognitive models of human memory beyond episodic memory, such as working memory.

Future research directions include extending the segmentation and boundary refinement processes to operate at each layer of the Transformer independently and exploring how EM-LLM could be utilized to enable imagination and future thinking.

Conclusion

EM-LLM represents a significant advancement in developing LLMs with extended context-processing capabilities. By integrating insights from cognitive science with machine learning, EM-LLM enhances the performance of LLMs on long-context tasks and provides a computational framework for testing hypotheses about human memory. The flexibility of this framework also suggests it could serve as a viable alternative to traditional RAG techniques, especially when combined with efficient compression methods.