Towards a theory of learning dynamics in deep state space models (2407.07279v1)

Abstract: State space models (SSMs) have shown remarkable empirical performance on many long sequence modeling tasks, but a theoretical understanding of these models is still lacking. In this work, we study the learning dynamics of linear SSMs to understand how covariance structure in data, latent state size, and initialization affect the evolution of parameters throughout learning with gradient descent. We show that focusing on the learning dynamics in the frequency domain affords analytical solutions under mild assumptions, and we establish a link between one-dimensional SSMs and the dynamics of deep linear feed-forward networks. Finally, we analyze how latent state over-parameterization affects convergence time and describe future work in extending our results to the study of deep SSMs with nonlinear connections. This work is a step toward a theory of learning dynamics in deep state space models.

• The paper demonstrates analytical solutions revealing that data covariance significantly affects convergence behavior in linear state space models.
• It uses frequency domain analysis to simplify learning dynamics and highlights parallels with deep linear feed-forward networks.
• The study finds that over-parameterization in latent states accelerates learning, offering insights for designing more efficient SSMs.

Towards a Theory of Learning Dynamics in Deep State Space Models

Introduction

State space models (SSMs) have demonstrated notable empirical efficacy in handling long sequence modeling tasks. Despite their success, a comprehensive theoretical framework for understanding their learning dynamics remains underdeveloped. This paper presents an investigation into the learning dynamics of linear SSMs, focusing on how data covariance structure, the size of latent states, and initialization influence the evolution of model parameters during gradient descent. The authors explore the learning dynamics in the frequency domain, which allows the derivation of analytical solutions under certain assumptions. This facilitates a connection between one-dimensional SSMs and the dynamics seen in deep linear feed-forward networks. The paper further assesses how latent state over-parameterization impacts convergence time, suggesting avenues for future exploration into extending these findings to nonlinear deep SSMs.

Learning Dynamics in the Frequency Domain

Linear time-invariant systems are central to the paper's analysis. The authors begin by considering a simple discrete-time SSM:

$x_t = Ax_{t-1} + Bu_t, \quad y_t = Cx_t,$

where $u_t$ is the input, $x_t$ is the latent state, and $y_t$ is the output. The parameters $A$, $B$, and $C$ govern the system dynamics. In the frequency domain, the parameters admit a simplified representation via the discrete Fourier transform (DFT), transforming the recurrence in the time domain to element-wise multiplication in the frequency domain. The learning dynamics under gradient descent are thereby reduced to operations involving the DFT of inputs and outputs, $U_k$ and $Y_k$.

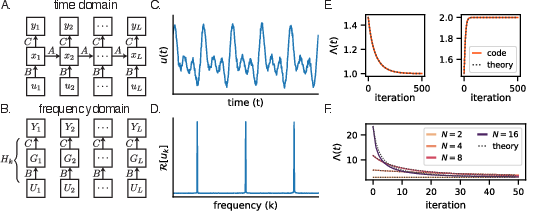
Figure 1: Learning dynamics of SSMs in the frequency domain.

Simplified Learning Dynamics

To simplify the analysis, the paper considers the case of a one-layer SSM, where $A$ is fixed, reducing the complexity of learning dynamics for parameters $B$ and $C$. They derive continuous-time dynamics equations under a squared error loss, resulting in simplified expressions that elucidate convergence behavior. The convergence is found to inversely relate to input-output covariances in the frequency domain, mirroring results from the paper of deep linear networks and reaffirming the connection between learning dynamics in these two domains.

Larger Latent State Sizes

The paper extends the analysis to $N$-dimensional models, proposing symmetric initialization across latent dimensions to mitigate error minima sensitivity induced by larger latent states. The convergence time becomes inversely proportional to both the latent state size $N$ and input-output covariances, suggesting that over-parameterization accelerates learning. This deeper exploration reveals links between multi-dimensional linear SSMs and deep feed-forward networks under specific assumptions, and provides a basis for future investigation into nonlinear SSMs with complex connection patterns.

Conclusion

This paper establishes analytical solutions for the learning dynamics of linear SSMs, connecting them to existing theories of deep linear networks' learning dynamics. The work emphasizes the implications of data covariance and latent structure on convergence time, preparing the groundwork for more intricate studies of multi-layer SSMs, potentially with nonlinear interactions. Future exploration is geared towards dissecting the role of parameterization in these complex systems, leveraging the foundational understanding generated by this paper to improve SSM design and inference in practical applications.

In summary, the work achieves a significant advance towards a complete theory of learning dynamics in SSMs, paving the way for enhanced model training and design strategies. Further investigations are required to explore nonlinear extensions, integrating the theoretical insights derived herein with practical advancements in complex system modeling.