Uncertainty-Guided Likelihood Tree Search (2407.03951v3)

Abstract: Tree search is a fundamental tool for planning, as many sequential decision-making problems can be framed as searching over tree-structured spaces. We propose an uncertainty-guided tree search algorithm for settings where the reward function is a log-likelihood function of the paths. Due to the combinatorial explosion of the tree size, the set of paths for which one can obtain rewards is sparse, particularly when the likelihood is obtained through expensive evaluations, such as by querying a LLM. We address this challenge by deriving an probabilistic search heuristic based on regularity assumptions for the likelihood. Unlike existing tree search methods, the proposed method can perform backtracking and trade-off exploration with exploitation, and yet does not require expensive roll-outs, or sophisticated Bayesian inference. Through extensive on-model and off-model experiments on timely, large-scale practical applications, we demonstrate that our method identifies paths with high likelihood while requiring fewer costly evaluations.

• The paper introduces ULTS, a method that uses uncertainty to optimize likelihood rewards in computationally expensive search spaces.
• It employs Dirichlet-based probabilistic modeling and a non-myopic acquisition function similar to Thompson sampling for effective tree navigation.
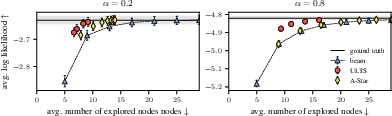
• Experiments show ULTS outperforms beam search and A* in both efficiency and effectiveness on synthetic data and LLM decoding tasks.

Uncertainty-Guided Likelihood Tree Search

Introduction

"Uncertainty-Guided Likelihood Tree Search" introduces a novel tree search algorithm designed to efficiently navigate large, expensive search spaces characterized by a likelihood reward function. The method leverages computational uncertainty to perform informed exploration within tree structures, significantly reducing the need for costly evaluations typical of conventional methods. The approach draws on principles from Bayesian optimization to balance exploration and exploitation without requiring extensive rollouts or complex Bayesian inference processes.

Problem Setting

The problem is framed within a Markov Decision Process (MDP) context, where the objective is to maximize a cumulative likelihood (log-reward) over paths in a tree-structured state space. This is particularly relevant in scenarios where reward evaluations, such as those from querying LLMs, are computationally expensive. The method addresses scenarios not adequately handled by traditional methods like beam search or Monte Carlo tree search (MCTS) due to these computational constraints.

Methodology

Probabilistic Framework: The approach builds on a probabilistic framework that models transition probabilities as samples from a Dirichlet distribution. This allows for a tractable, scalable incorporation of uncertainty directly into the tree search process. ULTS employs a non-myopic acquisition function akin to Thompson sampling to guide tree expansion based on posterior beliefs over node values.

Algorithmic Strategy: ULTS operates in four key steps:

1. Selection: Nodes are selected based on an acquisition function that integrates expected utility over descendant values, emphasizing paths that maximize these expected utilities.
2. Expansion: Once a node is selected, its children are expanded, and their rewards are evaluated, incorporating computational uncertainty to guide future selections.
3. Backup: Posterior samples obtained during expansion are recursively propagated up the tree, updating beliefs about the optimal values of all nodes in the path to influence subsequent selections.
4. Termination: The algorithm employs a probabilistic termination criterion based on the likelihood of current best paths, allowing it to stop when confident that no further exploration would yield better results.

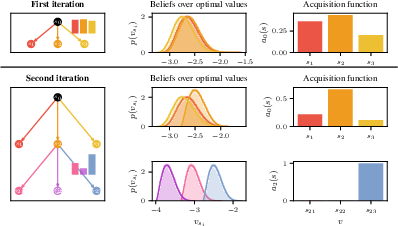
   Figure 1: An example of two iterations with ULTS. The upper row shows the observed categorical distribution (left), the implied posterior over the optimal values in log space (center), and the resulting acquisition function over the children in the first level of the tree (right). The lower two rows show the corresponding quantities for the first and second level of the tree after the second iteration.

Experiments

The authors conducted extensive experiments on both synthetic and real-world datasets, demonstrating the efficiency of ULTS in scenarios where traditional methods falter:

• Synthetic Data: Using trees with transition probabilities sampled from a Dirichlet distribution, ULTS outperformed beam search and A* in terms of efficiency and effectiveness, revealing its ability to capitalize on known probabilistic distributions.
• LLMs: Applied to LLM decoding tasks such as text generation and summarization, ULTS showcased significant reductions in node expansions while maintaining high likelihoods for generated sequences. It surpassed standard baselines, particularly in low-computation budget scenarios, underscoring its practical value in computationally constrained settings.

  Figure 2: Comparison of ULTS with beam search and A

  on synthetic rewards sampled from a Dirichlet distribution with $\alpha=0.2$ and $\alpha=0.8$. ULTS finds the optimum efficiently. Error bars indicate one times the standard error of the mean.*

Practical Implications and Limitations

ULTS provides a compelling tool for domains requiring efficient navigation of large decision trees with expensive node evaluations, particularly in autoregressive model applications beyond LLMs, like chemistry or robotics. However, its assumptions about reward distributions and computational limits may not generalize across all domains, necessitating further exploration of adaptive, context-aware strategies to expand its applicability.

Conclusion

Uncertainty-Guided Likelihood Tree Search represents a significant advance in probabilistic heuristic search, offering a streamlined approach to balancing exploration and exploitation on likelihood-structured decision problems. By efficiently managing computational uncertainty without heavy resource demands, ULTS sets the stage for broader application in environments necessitating strategic sequential decision-making under constraints. Future work could explore incorporating deeper model uncertainties and further enhancements to batch processing capabilities.