Compress then Serve: Serving Thousands of LoRA Adapters with Little Overhead (2407.00066v4)

Abstract: Fine-tuning LLMs with low-rank adaptations (LoRAs) has become common practice, often yielding numerous copies of the same LLM differing only in their LoRA updates. This paradigm presents challenges for systems that serve real-time responses to queries that each involve a different LoRA. Prior works optimize the design of such systems but still require continuous loading and offloading of LoRAs, as it is infeasible to store thousands of LoRAs in GPU memory. To mitigate this issue, we investigate the efficacy of compression when serving LoRAs. We propose a method for the joint compression of LoRAs into a shared basis paired with LoRA-specific scaling matrices. We extend our algorithm to learn clusters of LoRAs that are amenable to joint compression, allowing it to scale gracefully to large LoRA collections. Our experiments with up to 1000 LoRAs demonstrate that compressed LoRAs preserve performance while offering major throughput gains in realistic serving scenarios with over a thousand LoRAs, maintaining 80% of the throughput of serving a single LoRA.

• The paper introduces a framework that compresses large collections of LoRA adapters using independent SVD and joint diagonalization, reducing GPU memory demands.
• It demonstrates that both compression methods can retain over 90% of task performance while significantly lowering per-request overhead.
• Empirical integration with vLLM shows a throughput improvement of over 2×, enabling scalable multi-task deployments with minimal compute lag.

Efficient Compression and Serving of Large Collections of LoRA Adapters

Introduction and Motivation

The proliferation of downstream applications for LLMs has led to an unprecedented demand for specialized expert models, often implemented as low-rank adapters (LoRAs). These parameter-efficient fine-tuned modules enable rapid adaptation without the full cost of model retraining or storing a complete set of new weights per task. However, the need to serve thousands of LoRAs simultaneously in production, with low latency and minimal compute overhead, poses significant technical challenges. In particular, storing each LoRA adapter on GPU memory is infeasible at scale, and constantly moving adapters on and off the device results in degraded throughput. This work introduces a paradigm of compressing LoRA collections—evaluating both individual and joint compression methods—such that they can be efficiently served from a shared basis on GPU hardware, thereby supporting scalable multitask deployment.

Compression Techniques for LoRA Aggregation

The central contribution is a formal treatment of LoRA compression as a matrix reconstruction problem. Given a set of $n$ LoRAs, each parameterized by matrix pairs $(A_i, B_i)$ with rank $r_i$, the objective is to find compressed representations which—collectively—reduce memory and computation requirements for serving, while preserving task-specific performance.

Independent (Per-LoRA) Compression via SVD:

Each LoRA adapter is compressed individually using truncated SVD:

$B_i A_i \approx U_i \Sigma_i V_i^\top$

where $U_i$, $V_i$ capture the top-$r$ singular vectors. This approach attains optimal Frobenius-norm reconstruction for each LoRA independently, with parameter count scaling as $\mathcal{O}(n r d)$ for $n$ LoRAs of input/output dimension $d$. However, parameter sharing across LoRAs is not exploited, and as $n$ grows, memory savings become marginal—limiting scalability.

Joint Compression via Shared Subspace (Joint Diagonalization):

In contrast, joint diagonalization seeks a shared subspace representation:

$B_i A_i \approx U \Sigma_i V^\top$

with $U,V$ shared across all LoRAs and task-specific scaling (typically diagonal or low-rank) $\Sigma_i$. This allows $U,V$ to permanently reside in GPU memory, while only small adapter-specific matrices must be swapped in/out. As a result, the per-query overhead is reduced from loading two full-rank matrices per adapter to transferring only small $\Sigma_i$, notably increasing throughput at scale.

The critical trade-off is that strong compression (low shared subspace rank) may degrade the ability to reconstruct individual LoRA functions. Theoretically, the construction is lossless only if the shared subspace has rank at least $$\tilde{r} = \max\{\operatorname{rank}([A_1,\ldots,A_n]), \operatorname{rank}([B_1^T,\ldots,B_n^T])\}$$. In practice, with noise or diversity, the rank necessary for lossless recovery rapidly approaches $n r$.

Theoretical Analysis of Compression Trade-offs

The paper provides sharp theoretical lower and upper bounds relating the achievable reconstruction fidelity in the joint basis to the spectrum of the aggregate LoRA operator matrix $$L = [\mathrm{vec}(B_1A_1), \ldots, \mathrm{vec}(B_nA_n)]$$. When LoRAs are similar or clustered, they admit low-rank approximation; when LoRAs are nearly orthogonal, compression loss is significant unless the basis rank is high. Crucially, the link between adapter matrix approximation error and downstream model performance is nonlinear: the authors empirically observe highly sublinear performance loss with moderate reconstruction error, indicating that the compressed representations generalize well and may even act as a form of regularization (see below).

Empirical Results: Performance, Throughput, and Generalization

Task Performance:

The methods are evaluated on 500 expert LoRAs trained on natural instruction tasks with Mistral-7B-Instruct-v0.2 as base. Independent and joint compression both preserve, and sometimes marginally improve, task accuracy (ROUGE-L, cross-entropy, exact-match) up to very high compression rates. When compressing 500 LoRAs, even with significant parameter savings, compressed adapters retain over $90\%$ of relative performance.

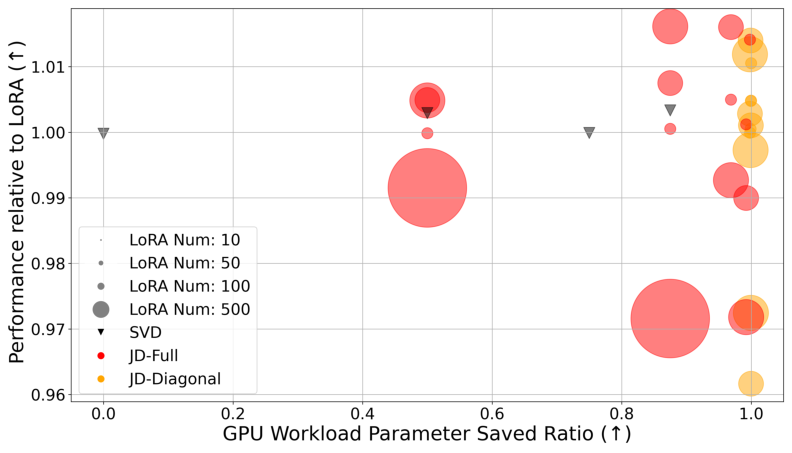
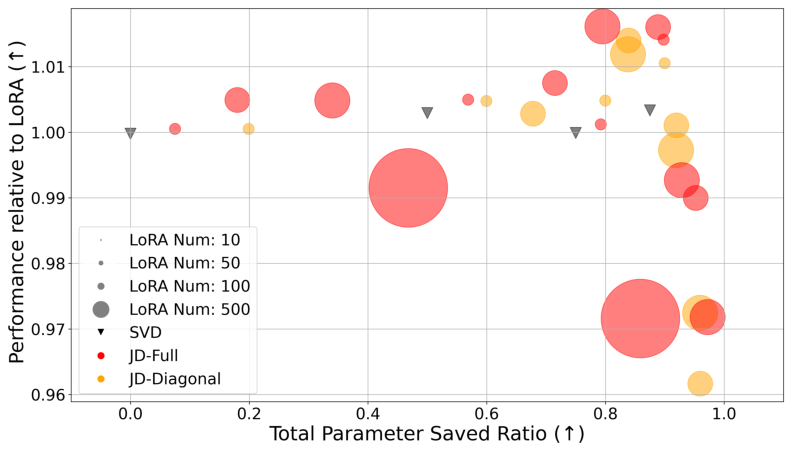
Figure 1: Performance relative to uncompressed LoRAs as a function of GPU parameter saved ratio. Both SVD and joint diagonalization methods enable strong compression with minimal loss.

Reconstruction Error vs. Performance:

There is a steep performance drop only beyond a critical threshold of reconstruction error, but mild lossy compression often preserves or slightly enhances downstream metrics, especially in out-of-distribution settings—supporting the hypothesis that dimensionality reduction can regularize overfitting to specific adapters.

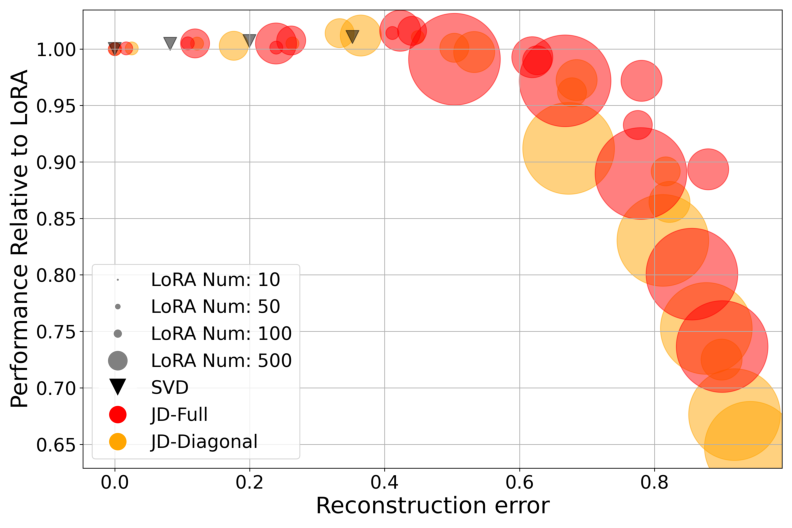
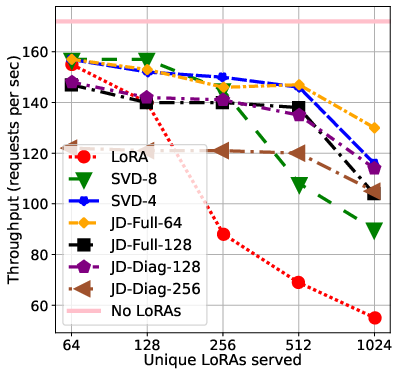
Figure 2: Downstream performance as a function of weight reconstruction error. Lossless reconstruction is not required to maintain high accuracy, suggesting robustness to compression noise.

Serving Throughput:

Integrating the compressed representations into vLLM—a state-of-the-art LLM serving architecture—demonstrates practical benefits. With >500 LoRAs, joint diagonalization methods achieve at least $2\times$ improvement in per-request throughput over uncompressed adapters, and at 1000+ LoRAs, maintain $75\%$ of the idealized single-LoRA throughput. The memory budget, and thus the scheduling bottleneck, is dramatically alleviated as only $\Sigma_i$ matrices need to be moved on/off the GPU. The underlying kernel implementations in vLLM require only minimal modification, indicating compatibility with existing deployment infrastructure.

Implementation Considerations and System Design

• Algorithmic Optimization: Joint diagonalization is solved using alternating least-squares or custom eigenvalue iteration schemes, with practical convergence achieved in <10 iterations for typical settings. Both full and diagonal $\Sigma_i$ matrices are supported, trading off representation power for additional parameter savings.
• GPU Kernel Integration: The compressed adapters are compatible with batched inference and can avoid the batched matrix multiplication bottleneck in multi-LoRA serving. Further low-level kernel optimization is possible.
• Adapter Norm Normalization: Normalizing $A_i,B_i$ matrices before basis construction reduces inter-task variance and improves shared subspace discovery and, consequently, performance robustness in OOD evaluation.
• Incremental Adaptation: When introducing new LoRAs, recompression of the shared basis is optimal but costly; newly introduced LoRAs can be projected into the existing basis at some performance loss. A hybrid solution is recommended: recompressing infrequently, and serving rare adapters in uncompressed form as needed.

Implications and Future Directions

Practically, these compression frameworks shift the bottleneck in multitask LLM serving from memory and compute I/O to subspace quality. The ability to serve thousands of experts from a memory footprint close to a single model unlocks new scaling regimes for personalized or tenant-specific assistants, high-throughput routing, and federated multi-domain deployments.

Theoretically, the empirical resilience to lossy compression calls for further investigation into the geometry of the LoRA solution manifold and its impact on transfer/interference. Connections to mode connectivity, model merging, and mixture-of-expert routing are immediate; questions remain as to whether algorithmic basis selection can exploit task clustering or other priors.

Downstream, integration of LoRA compression with quantized/low-precision adapters, routing policies, and out-of-distribution generalization promises to further increase efficiency and robustness. Improved scheduler designs could also dynamically select the compressed vs. uncompressed path on a per-request basis, considering workload and memory pressure.

Conclusion

This paper provides a comprehensive framework for compressing and efficiently deploying large collections of LoRA adapters. By leveraging individual and joint compression techniques, it demonstrates that thousands of LoRAs can be served with minimal overhead, retaining expert performance for diverse tasks while enabling near-optimal hardware utilization. These results contribute a foundation for practical, scalable, multi-expert LLM inference and motivate deeper theoretical analysis of the structure of LoRA-induced solution spaces.