Step-DPO: Step-wise Preference Optimization for Long-chain Reasoning of LLMs (2406.18629v1)

Abstract: Mathematical reasoning presents a significant challenge for LLMs due to the extensive and precise chain of reasoning required for accuracy. Ensuring the correctness of each reasoning step is critical. To address this, we aim to enhance the robustness and factuality of LLMs by learning from human feedback. However, Direct Preference Optimization (DPO) has shown limited benefits for long-chain mathematical reasoning, as models employing DPO struggle to identify detailed errors in incorrect answers. This limitation stems from a lack of fine-grained process supervision. We propose a simple, effective, and data-efficient method called Step-DPO, which treats individual reasoning steps as units for preference optimization rather than evaluating answers holistically. Additionally, we have developed a data construction pipeline for Step-DPO, enabling the creation of a high-quality dataset containing 10K step-wise preference pairs. We also observe that in DPO, self-generated data is more effective than data generated by humans or GPT-4, due to the latter's out-of-distribution nature. Our findings demonstrate that as few as 10K preference data pairs and fewer than 500 Step-DPO training steps can yield a nearly 3% gain in accuracy on MATH for models with over 70B parameters. Notably, Step-DPO, when applied to Qwen2-72B-Instruct, achieves scores of 70.8% and 94.0% on the test sets of MATH and GSM8K, respectively, surpassing a series of closed-source models, including GPT-4-1106, Claude-3-Opus, and Gemini-1.5-Pro. Our code, data, and models are available at https://github.com/dvlab-research/Step-DPO.

• The paper introduces Step-DPO, an approach that refines preference optimization by focusing on individual reasoning steps in long-chain problems.
• It employs a three-stage data construction pipeline to generate about 10K step-wise preference pairs, ensuring effective in-distribution training.
• Experimental results demonstrate nearly a 3% accuracy gain on the MATH dataset, aligning LLM reasoning closer to human-level performance.

Step-DPO: Enhancing Mathematical Reasoning in LLMs

Introduction

The paper "Step-DPO: Step-wise Preference Optimization for Long-chain Reasoning of LLMs" addresses the challenge of mathematical reasoning in LLMs by proposing Step-DPO as an improvement over Direct Preference Optimization (DPO). The key issue with DPO lies in its inadequacy in handling errors within long-chain reasoning tasks, particularly in mathematics, where the correctness of each step is crucial. Step-DPO refines this by optimizing preference at the reasoning step level, allowing for finer supervision and correction of errors as they arise.

Step-DPO Approach

The Step-DPO framework treats individual reasoning steps as preference optimization units rather than evaluating answers holistically. This methodology is essential in long-chain reasoning tasks where errors often manifest in intermediate steps. By focusing on correcting the first erroneous step, Step-DPO enhances the model's ability to learn the correct reasoning trajectory.

This refinement allows models to significantly improve their accuracy on mathematical datasets like MATH and GSM8K, particularly in handling complex problems requiring extensive reasoning chains.

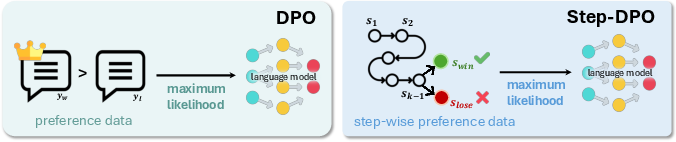
Figure 1: Comparison between DPO and Step-DPO.

Data Construction Pipeline

To support Step-DPO, the paper introduces an effective data construction pipeline that efficiently assembles a high-quality dataset. This pipeline involves three key stages: error collection, step localization, and rectification. In the error collection phase, mathematical problems with incorrect model-generated solutions are identified. The step localization phase detects the first erroneous reasoning step through either manual verification or the use of ATI tools like GPT-4. Finally, rectification involves generating correct reasoning steps using the reference model, ensuring the data remains in-distribution.

The pipeline demonstrates a streamlined process for generating approximately 10K step-wise preference pairs, allowing models to learn from detailed reasoning errors and preferred in-distribution solutions.

Figure 2: Data construction pipeline for Step-DPO.

Figure 3: An example of preference data sample for Step-DPO.

Experimental Results

Step-DPO shows substantial improvements in mathematical reasoning for models with over 70B parameters, delivering nearly a 3\% gain in accuracy on the MATH dataset. The method aligns models more closely with human-level reasoning, achieving higher benchmark scores compared to previous state-of-the-art models including GPT-4-1106 and Claude-3-Opus.

The paper provides an in-depth analysis, showcasing how Step-DPO maintains accuracy with fewer than 500 training steps and a significantly smaller dataset, emphasizing its efficiency in data utilization and training resource management.

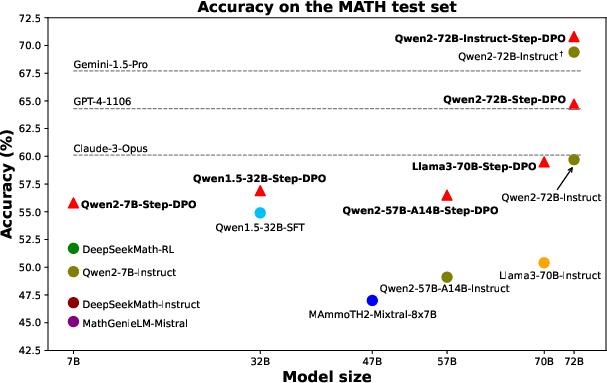
Figure 4: Accuracy on the MATH test set across models fine-tuned by Step-DPO and other state-of-the-art models. ^\dagger: reproduced result using our prompt.

Conclusion

Step-DPO presents a meaningful advancement in the alignment and training of LLMs for complex reasoning tasks, specifically within mathematics. By refining the approach to preference optimization at a granular level and leveraging efficient data construction methods, Step-DPO proves to be an effective tool in enhancing the accuracy of mathematical reasoning in LLMs. The research invites further exploration into similarly structured optimization techniques across various reasoning-sensitive domains, with potential applications in AI-driven educational tools and automated reasoning systems.

Figure 5: An example of comparison between Qwen2-72B-Instruct and Qwen2-72B-Instruct-Step-DPO.