Convolutional Kolmogorov-Arnold Networks (2406.13155v3)

Abstract: In this paper, we present Convolutional Kolmogorov-Arnold Networks, a novel architecture that integrates the learnable spline-based activation functions of Kolmogorov-Arnold Networks (KANs) into convolutional layers. By replacing traditional fixed-weight kernels with learnable non-linear functions, Convolutional KANs offer a significant improvement in parameter efficiency and expressive power over standard Convolutional Neural Networks (CNNs). We empirically evaluate Convolutional KANs on the Fashion-MNIST dataset, demonstrating competitive accuracy with up to 50% fewer parameters compared to baseline classic convolutions. This suggests that the KAN Convolution can effectively capture complex spatial relationships with fewer resources, offering a promising alternative for parameter-efficient deep learning models.

• The paper presents a novel convolutional architecture that integrates adaptive B-spline functions within CNN kernels to reduce parameters while retaining accuracy.
• The methodology leverages the Kolmogorov-Arnold theorem to replace fixed activations with dynamic, learnable splines for enhanced feature extraction.
• Experimental results on MNIST and Fashion-MNIST demonstrate that the proposed models achieve comparable accuracy to standard CNNs with a reduced parameter count.

Convolutional Kolmogorov-Arnold Networks

Introduction

The paper introduces Convolutional Kolmogorov-Arnold Networks (Convolutional KANs), a novel approach intended to enhance the efficiency and parameter reduction in convolutional network architectures within computer vision tasks. Leveraging the Kolmogorov-Arnold Networks methodology, this paper integrates spline-based layers into traditional convolutional structures to create more adaptable and memory-efficient models. The primary aim is to maintain competitive accuracy levels while significantly reducing the number of model parameters required, opening up pathways for optimizing neural network designs.

Kolmogorov-Arnold Networks (KANs)

KANs utilize the Kolmogorov-Arnold representation theorem, asserting that any multivariate continuous function can be represented through compositions of univariate functions and additions, thereby allowing neural networks to implement adaptive, learnable splines in lieu of fixed activation functions. This architecture enables networks to handle data complexity with fewer parameters and improved generalization capabilities.

Figure 1: Splines learned by the first convolution at the first position for different ranges, illustrating the behavior within and outside defined range limits.

Convolutional KAN Architecture

This adaptation into convolutional layers—termed KAN Convolutions—replaces traditional kernels made from static weight matrices with dynamic, learnable spline functions. These splines, defined as B-Splines, are embedded within kernels to capture complex spatial relationships more effectively than linear approaches.

Implementation of KAN Convolutions involves calculating dot products between image data points and learnable spline functions, providing enhanced expressiveness in feature extraction.

Experimental Setup and Results

The paper describes a series of experiments comparing KAN-based architectures against standard CNN models using MNIST and Fashion-MNIST datasets. The architectures are detailed, showcasing variations in convolutional kernels and activations across different scenarios.

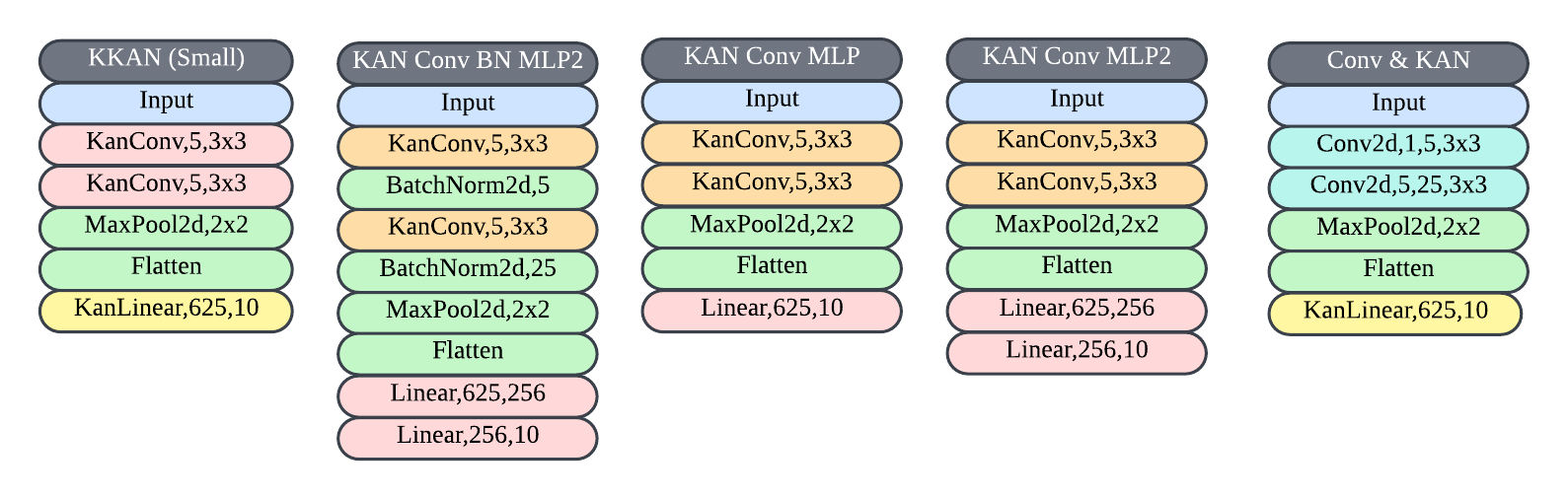
Figure 2: Convolutional KAN Architectures used in experiments demonstrating alternative configurations.

Figure 3: Standard Architectures used in experiments, serving as benchmarks against the proposed models.

The results highlight that the proposed Convolutional KAN models achieve comparable accuracy with a reduced parameter count, demonstrating effective learning capabilities even with fewer layers and resources.

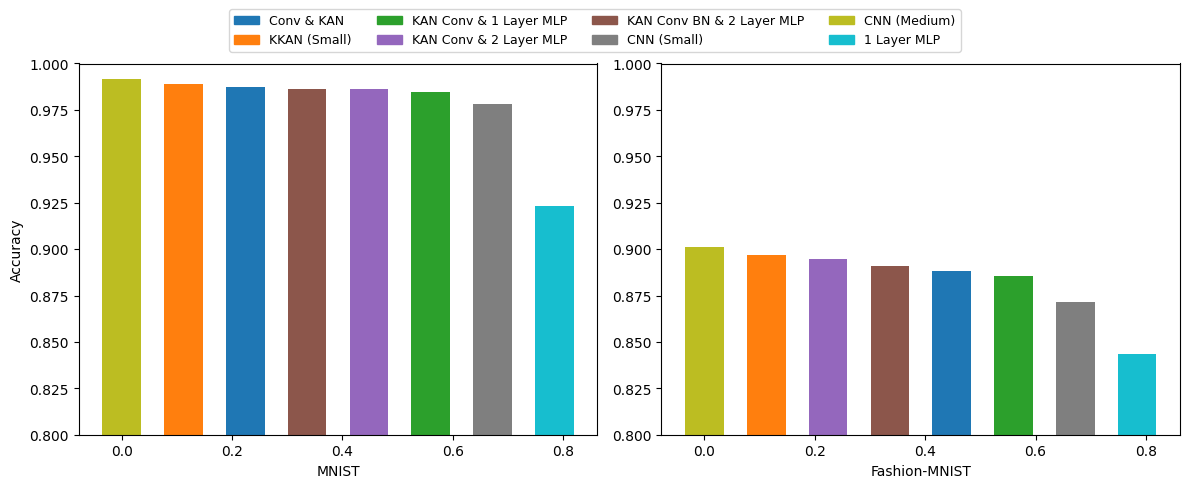
Figure 4: Accuracy on MNIST and Fashion MNIST, indicating superior performance of proposed models over CNN (Small) and similar results compared to CNN (Medium).

Discussion and Interpretation

One crucial advantage of Convolutional KANs lies in their reduced parameter necessity; by utilizing splines, they achieve significant flexibility in spatial data representation. Although they exhibit slower training times due to the overhead of optimizing spline functions, they compensate with lower parameter usage, maintaining accuracy levels akin to more complex models.

Despite their promising performance, interpretability of spline behavior in KAN Convolutions remains unclear, marking a direction for further research.

Conclusion

Convolutional Kolmogorov-Arnold Networks offer a compelling alternative to traditional CNN architectures by integrating adaptive spline-based convolutions. These networks retain high accuracy with fewer parameters, paving the way for more efficient architectures in computer vision. Future research should explore the interpretability of spline functions and optimize these models for better scalability and faster training times.

Future Work

The ongoing development of Convolutional KANs will involve expanding evaluation across more complex datasets like CIFAR10 and ImageNet, investigating spline behavior to enhance interpretability, and optimizing training efficiency for larger scale applications.