GW-MoE: Resolving Uncertainty in MoE Router with Global Workspace Theory (2406.12375v1)

Abstract: Mixture-of-Experts (MoE) has been demonstrated as an efficient method to scale up models. By dynamically and sparsely selecting activated experts, MoE can effectively reduce computational costs. Despite the success, we observe that many tokens in the MoE models have uncertain routing results. These tokens have nearly equal scores for choosing each expert, and we demonstrate that this uncertainty can lead to incorrect selections. Inspired by the Global Workspace Theory (GWT), we propose a new fine-tuning method, GW-MoE, to address this issue. The core idea is to broadcast the uncertain tokens across experts during fine-tuning. Therefore, these tokens can acquire the necessary knowledge from any expert during inference and become less sensitive to the choice. GW-MoE does not introduce additional inference overhead. We validate that GW can mitigate the uncertain problem and consistently improve in different tasks (text classification, question answering, summarization, code generation, and mathematical problem solving) and model sizes (650M and 8B parameters).

• The paper introduces GW-MoE, a fine-tuning method inspired by Global Workspace Theory to broadcast uncertain tokens and reduce routing uncertainty.
• The methodology employs normalized entropy to identify uncertain tokens, allowing all experts to process them during fine-tuning.
• Empirical results across NLP tasks show improved performance on models from 650 million to 8 billion parameters without added inference costs.

GW-MoE: Resolving Uncertainty in MoE Router with Global Workspace Theory

The paper "GW-MoE: Resolving Uncertainty in MoE Router with Global Workspace Theory" (arXiv ID: (2406.12375)) investigates the challenge of uncertainty in Mixture-of-Experts (MoE) models, which arises when tokens are routed with nearly uniform scores amongst experts. The authors propose a novel fine-tuning approach inspired by Global Workspace Theory (GWT) that mitigates this uncertainty by broadcasting uncertain tokens to all experts during the fine-tuning process. This paper provides a comprehensive evaluation across several language tasks and model sizes, demonstrating the effectiveness of the proposed method.

MoE Model Uncertainty

Mixture-of-Experts models have gained traction due to their ability to scale up models effectively by activating a sparse subset of model parameters. In conventional MoE approaches, the router determines which experts are activated based on the tokens. The challenge arises when certain tokens, termed as 'uncertain tokens', have near-equal routing scores across potential experts, leading to random or suboptimal expert selections. This uncertainty potentially deteriorates the performance by preventing tokens from accessing precise knowledge encoded in the experts.

Global Workspace Theory as a Solution

Global Workspace Theory (GWT) posits that in the human brain, complex signals broadcast across a global workspace allow different functional modules to cooperate. Leveraging this concept, the authors suggest that uncertain tokens should similarly broadcast during model fine-tuning. The broadcasting helps ensure that these tokens can gather necessary information from any expert during inference, thereby reducing the sensitivity to specific expert choices.

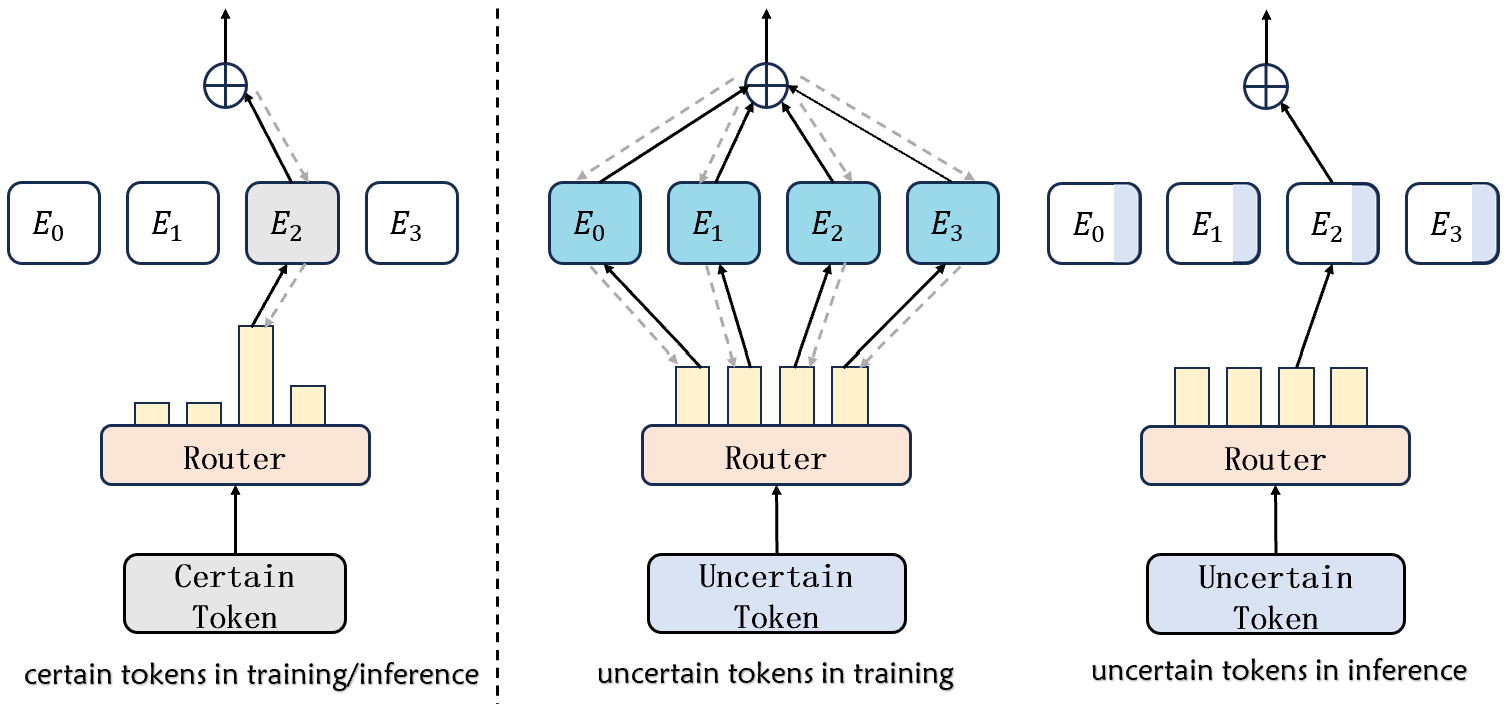
Figure 1: Illustration of GW-MoE inspired by Global Workspace Theory, where uncertain tokens are broadcast to all experts during fine-tuning.

Methodology

Identifying Uncertain Tokens

The uncertainty of a token is quantified using normalized entropy, calculated from the router's score distribution for each token. Tokens with entropies exceeding a defined threshold (e.g., a value corresponding to the top 5% of the entropy distribution) are treated as uncertain. These tokens are broadcast during fine-tuning, ensuring all experts learn relevant knowledge.

Fine-Tuning with GW-MoE

The GW-MoE method modifies standard MoE fine-tuning by processing uncertain tokens with all experts, while certain tokens are routed to the top-K experts. This dual mechanism ensures that during inference, the uncertain tokens can still access the requisite knowledge without additional computational cost.

Experimental Results

Experiments conducted across various natural language processing tasks, such as text classification and summarization, highlight the efficacy of GW-MoE. The approach consistently outperforms standard fine-tuning across models of different scales, from 650 million to 8 billion parameters, without introducing extra inference overhead.

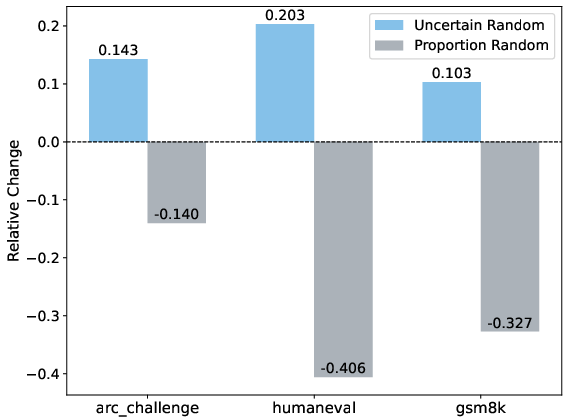
Figure 2: Results showing better performance when uncertain tokens select experts randomly compared to deterministic methods.

The empirical evaluations indicate that uncertain tokens, when broadcast during fine-tuning, lead to improved model performance. More specifically, tokens that were uncertain could benefit from obtaining knowledge from any expert, thus mitigating the negative impact of incorrect expert assignments.

Discussion and Future Work

The GW-MoE approach provides an important advancement in handling uncertainty within MoE models by leveraging concepts from cognitive science. The results affirm that broadcasting uncertain tokens during fine-tuning is a viable strategy to enhance model performance without additional inference costs.

Future investigations could explore the application of GW-MoE during the initial training phases of MoE models, as well as its potential for adaptation in even larger models beyond billions of parameters. Additionally, while effective for certain tasks, further fine-tuning strategies could be explored to address models' difficulties in language understanding tasks involving complex semantic relationships.

Conclusion

The introduction of the GW-MoE method presents a robust approach to dealing with expert selection uncertainty in MoE models. It effectively uses insights from GWT to improve the learning and inference processes for uncertain tokens, ensuring enhanced model performance across several benchmarks without increasing computational demands during inference. This novel methodology offers a valuable perspective on improving routing mechanisms and highlights new pathways for advancing MoE models' cognitive capabilities.