BSRBF-KAN: A combination of B-splines and Radial Basis Functions in Kolmogorov-Arnold Networks (2406.11173v5)

Abstract: In this paper, we introduce BSRBF-KAN, a Kolmogorov Arnold Network (KAN) that combines B-splines and radial basis functions (RBFs) to fit input vectors during data training. We perform experiments with BSRBF-KAN, multi-layer perception (MLP), and other popular KANs, including EfficientKAN, FastKAN, FasterKAN, and GottliebKAN over the MNIST and Fashion-MNIST datasets. BSRBF-KAN shows stability in 5 training runs with a competitive average accuracy of 97.55% on MNIST and 89.33% on Fashion-MNIST and obtains convergence better than other networks. We expect BSRBF-KAN to open many combinations of mathematical functions to design KANs. Our repo is publicly available at: https://github.com/hoangthangta/BSRBF_KAN.

• The paper introduces BSRBF-KAN, integrating B-splines and RBFs into KAN architectures to enhance function approximation and training stability.
• The methodology leverages the Kolmogorov-Arnold theorem by combining B-spline and Gaussian RBF activations, yielding rapid convergence and competitive 97.55% accuracy on MNIST.
• The ablation study demonstrates that the combined basis functions significantly contribute to network performance, suggesting further potential for complex dataset applications.

BSRBF-KAN: Integration of B-splines and Radial Basis Functions in Kolmogorov-Arnold Networks

Introduction

The paper "BSRBF-KAN: A combination of B-splines and Radial Basis Functions in Kolmogorov-Arnold Networks" introduces an innovative approach to enhancing the architecture of Kolmogorov-Arnold Networks (KANs) by integrating B-splines and Radial Basis Functions (RBFs). Kolmogorov-Arnold Networks have gained traction as they offer an alternative perspective to traditional Multi-Layer Perceptrons (MLPs), guided by the Kolmogorov-Arnold representation theorem (KART). This theorem allows the decomposition of multivariate continuous functions into a combination of single-variable functions and additions. BSRBF-KAN aims to leverage the adaptability and smoothness offered by B-splines and RBFs in its network design, with experimental validation conducted using the MNIST dataset.

Methodology

Kolmogorov-Arnold Representation Theorem

At the heart of KANs lies the Kolmogorov-Arnold representation theorem, which facilitates representing a multivariate continuous function $f(\mathbf{x})$ defined over $n$ variables as a sum of continuous single-variable functions. Expressed as:

$$f(\mathbf{x}) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^{n} \phi_{q,p}(x_p) \right)$$

the theorem sets the foundation for constructing networks that can ideally exceed typical MLP architectures by exploiting the flexibility of activation functions and architectures.

Design and Implementation

The design of BSRBF-KAN is grounded on the incorporation of B-splines and Gaussian RBFs into the function matrix $\Phi_{l}$ of a KAN layer. This matrix encapsulates transformations between successive layers of nodes, enhancing the network's capability for approximation via smooth, continuous transformations. For practical implementation, B-splines and RBFs are combined in activation functions to contribute to pre-activations as follows:

$$\phi(x) = w_b b(x) + w_s (\phi_{BS}(x) + \phi_{RBF}(x))$$

This formulation enables the integration of both types of basis functions, accommodating the diverse needs of function approximations within the network layers.

Experimental Evaluation

The paper evaluates BSRBF-KAN alongside known counterparts like FastKAN, FasterKAN, EfficientKAN, and GottliebKAN on the MNIST dataset. The networks were structured to include a hidden layer and hyperparameters consistent across models such as learning rate and optimizer.

Performance Results

BSRBF-KAN - showing a competitive average accuracy of 97.55% over five trials - achieved full training accuracy in contrast to its peers. While GottliebKAN achieved marginally higher accuracy, it demonstrated variability in results.

The analysis of training and validation losses illustrated BSRBF-KAN's rapid convergence within the early epochs, maintaining stable training dynamics as depicted below.

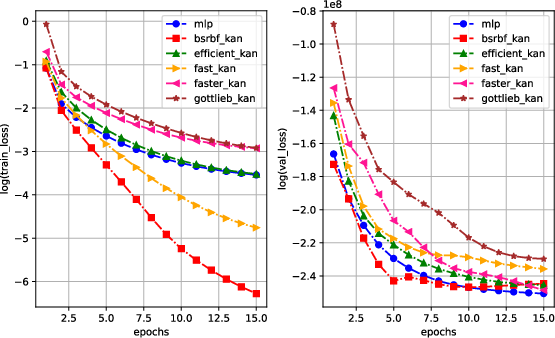
Figure 1: The logarithm values of training losses (left) and validation losses (right) in 15 epochs.

Ablation Study

The ablation paper explores the contribution of individual components within BSRBF-KAN. Results underscore the importance of base output and layer normalization, as their removal leads to significant degradation of performance metrics. While B-splines and RBFs independently provide marginal gains, their collective presence enriches approximation capabilities without significantly hampering stability.

Conclusion

BSRBF-KAN amalgamates B-splines and RBFs into KANs to harness the smooth and adaptive nature of these functions for training data convergence and stability. Although the approach does not drastically outperform conventional MLPs regarding accuracy, it highlights the potential for combining mathematical functions within KAN architectures. Future research aims to extend these concepts to more complex datasets and adjusted architecture variations to optimize performance further. The public availability of the implementation facilitates broader exploration and experimentation by the community.