Continuum Attention for Neural Operators (2406.06486v3)

Abstract: Transformers, and the attention mechanism in particular, have become ubiquitous in machine learning. Their success in modeling nonlocal, long-range correlations has led to their widespread adoption in natural language processing, computer vision, and time series problems. Neural operators, which map spaces of functions into spaces of functions, are necessarily both nonlinear and nonlocal if they are universal; it is thus natural to ask whether the attention mechanism can be used in the design of neural operators. Motivated by this, we study transformers in the function space setting. We formulate attention as a map between infinite dimensional function spaces and prove that the attention mechanism as implemented in practice is a Monte Carlo or finite difference approximation of this operator. The function space formulation allows for the design of transformer neural operators, a class of architectures designed to learn mappings between function spaces. In this paper, we state and prove the first universal approximation result for transformer neural operators, using only a slight modification of the architecture implemented in practice. The prohibitive cost of applying the attention operator to functions defined on multi-dimensional domains leads to the need for more efficient attention-based architectures. For this reason we also introduce a function space generalization of the patching strategy from computer vision, and introduce a class of associated neural operators. Numerical results, on an array of operator learning problems, demonstrate the promise of our approaches to function space formulations of attention and their use in neural operators.

• The paper introduces a continuous attention mechanism that redefines transformer architectures to operate on infinite-dimensional function spaces.
• The paper establishes the first universal approximation theorem for transformer neural operators, proving their ability to map complex, high-dimensional function spaces.
• The paper presents an efficient patch-based strategy to reduce computational complexity, achieving competitive performance on PDE problems like Darcy flow and Navier-Stokes equations.

Continuum Attention for Neural Operators

The paper explores the use of the attention mechanism, a staple in transformer architectures, within the field of neural operators. Neural operators map function spaces onto function spaces, making them both nonlinear and nonlocal. This research broadens the attention mechanism's application by interpreting it in the continuous domain of functions, thus integrating it into neural operators' frameworks.

Attention Mechanism in Function Spaces

Transformers have traditionally excelled at modeling discrete sequences in NLP, computer vision, and time series by effectively capturing long-range dependencies. By contrast, this paper extends the concept of attention to function spaces, treating attention as an operator that acts over these spaces. The attention mechanism is redefined as a Monte Carlo approximation of an operator between infinite-dimensional function spaces. This allows for the introduction of transformer neural operators, which provide mappings between such spaces and demonstrate universal approximation properties.

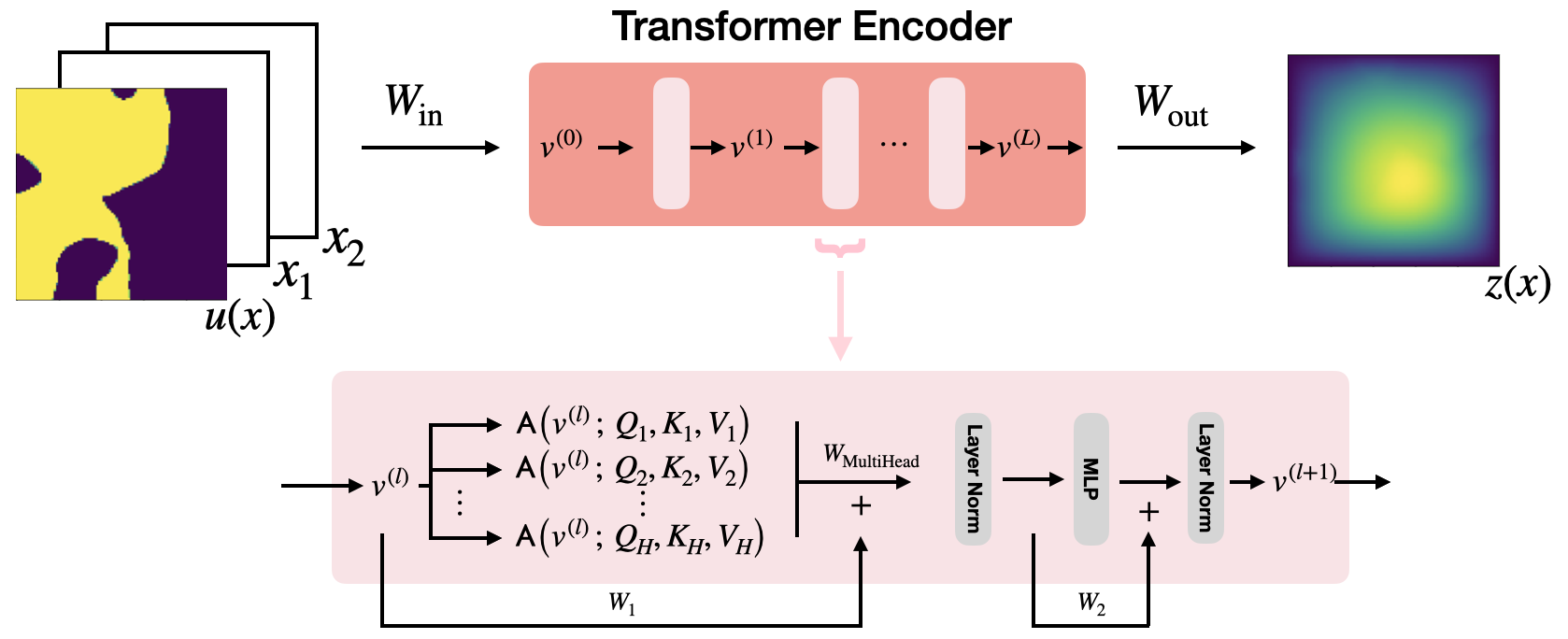
Figure 1: Transformer Neural Operator.

Universal Approximation Theorem for Neural Operators

A key theoretical contribution of this work is the establishment of the first universal approximation theorem for transformer neural operators. This theorem proves that with minor modifications to the traditional transformer architecture, these neural operators can universally approximate continuous functions. The practical implication is that such architectures can learn mappings from large, high-dimensional function spaces to other function spaces, a significant advantage in modeling complex physical systems described by PDEs.

The theorem leverages the nonlocal and nonlinear nature of the attention mechanism, reinforcing its ability to achieve universal approximation theorems in the context of neural operators. This is a significant step forward, as it bridges a gap between the empirical performance of transformers and rigorous mathematical guarantees.

Efficient Architectures and Numerical Results

Given the high computational complexity of applying the attention operator in multi-dimensional domains, the paper introduces a function space generalization of the patching strategy from computer vision. This efficiently reduces the quadratic scaling associated with attention mechanisms. The proposed architectures are particularly suited for scenarios where discretization invariance is desired, such as solving PDEs across different resolutions without retraining the model.

Figure 2: Vision Transformer Neural Operator.

Numerical experiments reveal that these transformer neural operators can match or outperform state-of-the-art methods in learning the solution operators to parametric PDEs. The research provides empirical evidence from experiments involving Lorenz 63 systems and controlled ODEs, demonstrating significant error reduction and stability across different tasks. 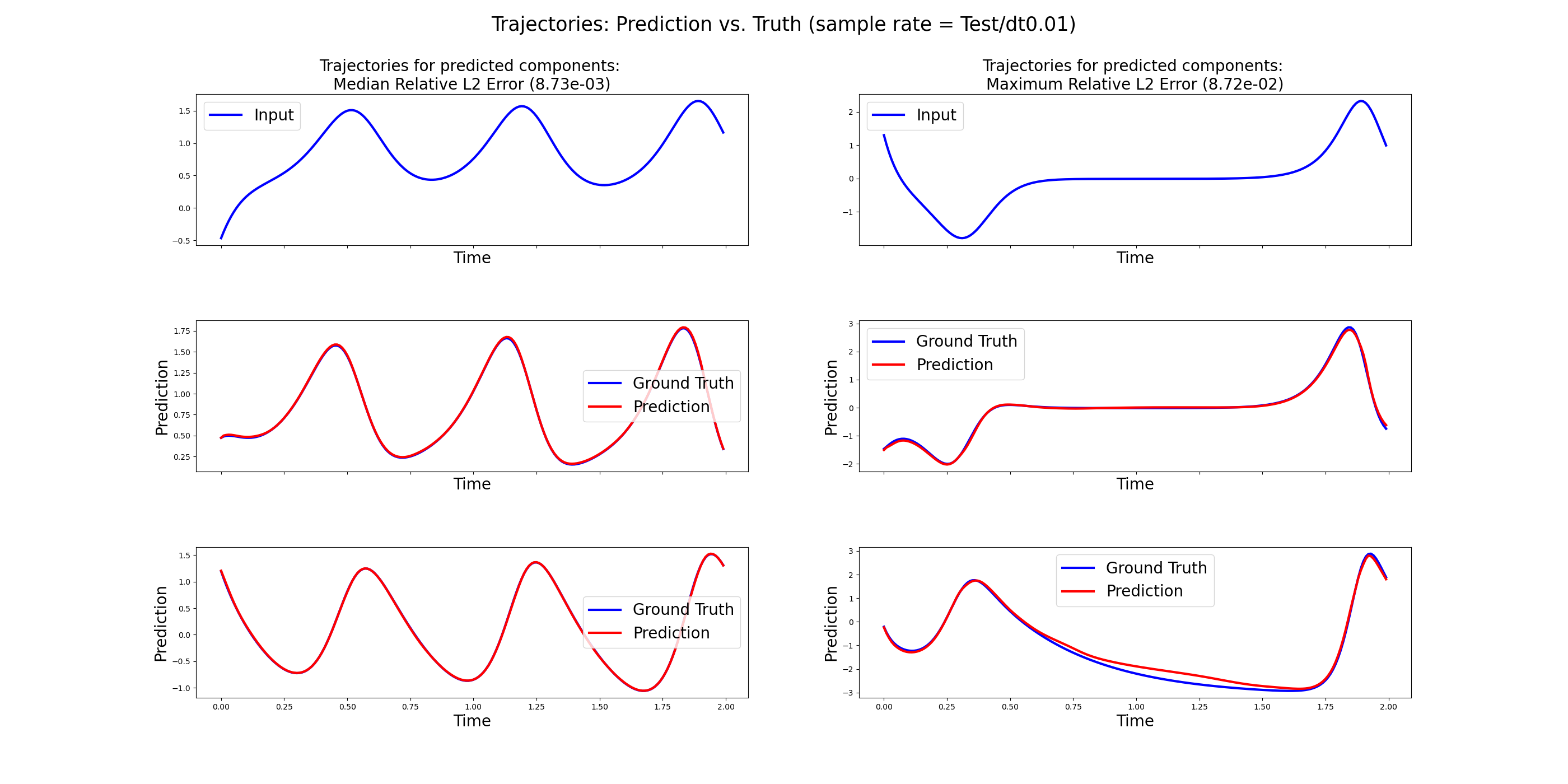![Figure 3](https://emergentmind-storage-cdn-c7atfsgud9cecchk.z01.azurefd.net/paper-images/2406-06486/x_to_yz.png) *Figure 3: The panel displays the performance of the transformer neural operator when applied to the Lorenz63 operator learning problem of recovering both unobserved y and z trajectories.*

Application to PDE Problems

The application of neural operators to PDE problems, like Darcy flow and Navier-Stokes equations, illustrates the practical benefits of attention-based neural operators. These neural operators can learn solution operators to parametric PDEs and can be applied to solve inverse problems and data assimilation tasks efficiently.

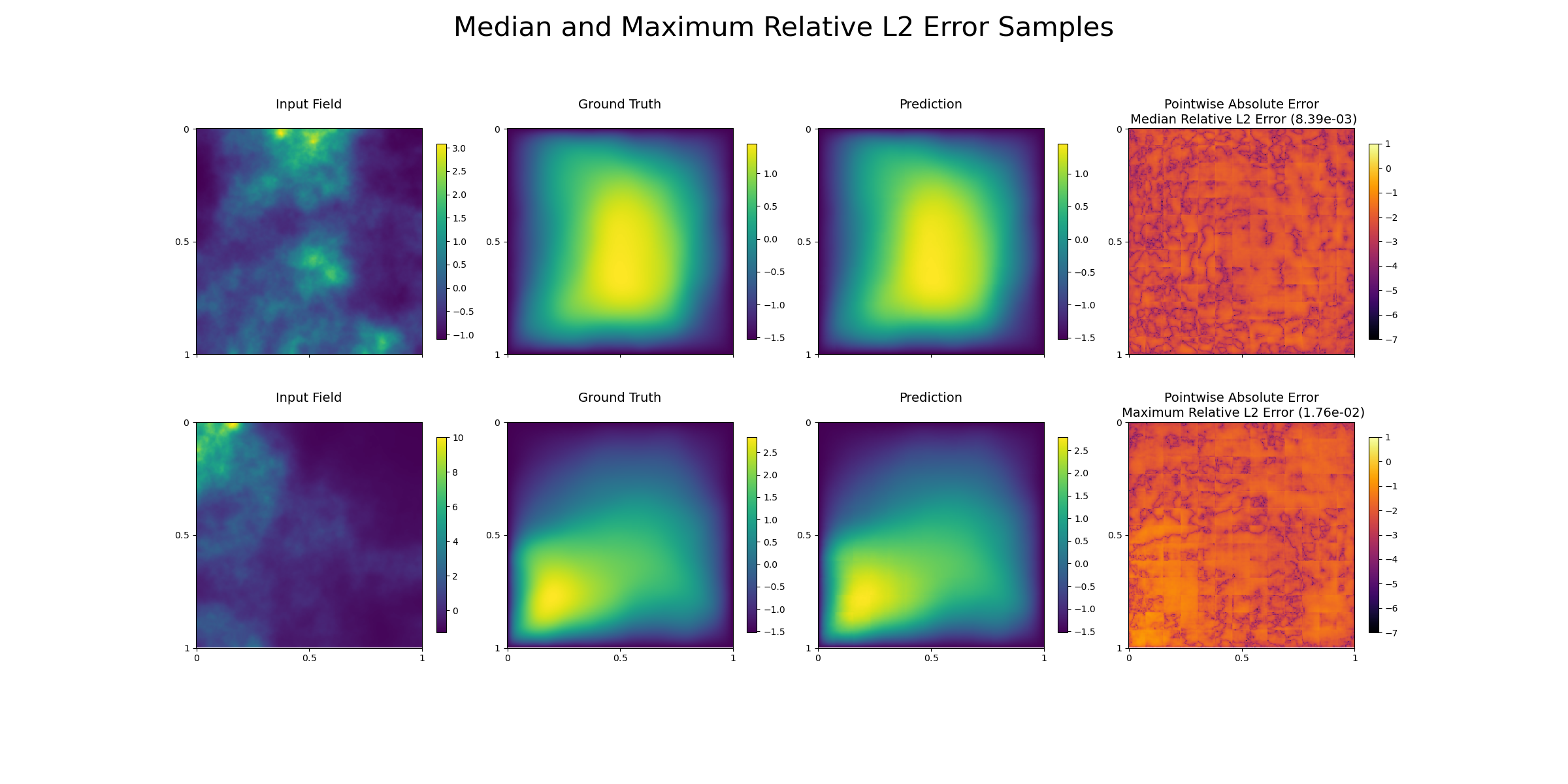
Figure 4: The panel displays the result of the application of the Fourier attention neural operator on the Darcy flow experiment with lognormal diffusion for the median and maximum relative L^2 error samples.

Conclusion

The paper presents a compelling extension of transformer architectures into the domain of neural operators, providing a framework that supports efficient and robust function space mappings. This advancement not only contributes to the theoretical understanding of attention in infinite-dimensional spaces but also opens avenues for practical applications in modeling complex systems with neural operators. Through the continuous attention mechanism and the novel transformer neural operator designs, the research sets the stage for further developments in both machine learning theory and PDE-based applications.