Geometric sparsification in recurrent neural networks

Abstract: A common technique for ameliorating the computational costs of running large neural models is sparsification, or the pruning of neural connections during training. Sparse models are capable of maintaining the high accuracy of state of the art models, while functioning at the cost of more parsimonious models. The structures which underlie sparse architectures are, however, poorly understood and not consistent between differently trained models and sparsification schemes. In this paper, we propose a new technique for sparsification of recurrent neural nets (RNNs), called moduli regularization, in combination with magnitude pruning. Moduli regularization leverages the dynamical system induced by the recurrent structure to induce a geometric relationship between neurons in the hidden state of the RNN. By making our regularizing term explicitly geometric, we provide the first, to our knowledge, a priori description of the desired sparse architecture of our neural net, as well as explicit end-to-end learning of RNN geometry. We verify the effectiveness of our scheme under diverse conditions, testing in navigation, natural language processing, and addition RNNs. Navigation is a structurally geometric task, for which there are known moduli spaces, and we show that regularization can be used to reach 90% sparsity while maintaining model performance only when coefficients are chosen in accordance with a suitable moduli space. Natural language processing and addition, however, have no known moduli space in which computations are performed. Nevertheless, we show that moduli regularization induces more stable recurrent neural nets, and achieves high fidelity models above 90% sparsity.

• The paper introduces moduli regularization that embeds neurons in a metric space to induce structured sparsity in RNNs.
• It demonstrates up to 90%-98% sparsity in navigation and NLP tasks, maintaining model stability and performance.
• The method challenges traditional L1 regularization by leveraging geometric relationships to align with underlying dynamical systems.

Geometric Sparsification in Recurrent Neural Networks

Introduction

The paper "Geometric sparsification in recurrent neural networks" (2406.06290) addresses the challenge of improving computational efficiency in recurrent neural networks (RNNs) through novel sparsification techniques. Sparsification, the removal of neural connections during training, has been essential for reducing the computational cost while maintaining model accuracy. The authors propose moduli regularization combined with magnitude pruning as a new sparsification method, leveraging topology to induce geometric relationships among neurons in hidden states, thus providing an a priori description of desired sparse architectures. This technique is validated on navigation and natural language processing tasks, showing high sparsity levels while maintaining performance.

Continuous Attractors

RNNs are often viewed as discrete approximations of dynamical systems on $\BR^n$, where the hidden state evolves according to vector field dynamics. Continuous attractors, representing stable loci along this vector field, are crucial in understanding RNN behavior. The paper's moduli regularization approach embeds neurons into a metric space to reflect this dynamical structure, effectively inducing sparse connectivity that respects geometric relationships. This contrasts with traditional $L_1$ regularization, aiming to minimize weight magnitudes without explicit geometric considerations.

Figure 1: Diagrammatic structure of the Elman RNN, with hidden state neurons embedded into a moduli space.

Moduli Regularization Framework

The core innovation is moduli regularization, which penalizes weights based on neuron distances within a moduli space. By embedding neurons into a chosen manifold, connections reflect geometric continuity, promoting sparsity aligned with the underlying RNN dynamics. Various manifolds, such as the circle, sphere, torus, and Klein bottle, are explored as moduli spaces. Optimal sparsification arises from embeddings suited to task-specific moduli spaces, though NLP lacks a clear geometric space, contrasting with navigation tasks.

Figure 2: Red points depict output neurons with low regularizing values, leading to potentially large weights, while blue points indicate smaller weights.

Results and Implications

Experiments show that moduli regularization offers robust sparsification, achieving up to 90% sparsity in navigation RNNs and 98% in NLP tasks without substantial performance loss. The approach yields sparse architectures that remain stable upon weight reinitialization, challenging the Lottery Ticket Hypothesis' notion of instability in sparse training. In navigation, the torus and Klein bottle provide superior regularization due to their geometric congruity with task space. For NLP, despite lacking a natural geometric framework, moduli regularizers enhance model stability and sparse performance compared to random or traditional methods.

Figure 3: Heatmap of neural weights in a navigation RNN, demonstrating geometric sparsification effects.

Conclusion

The paper presents moduli regularization as a transformative approach in sparsifying RNNs, aligning computational models with underlying geometric structures. This method not only reduces computation costs but enhances model stability—a significant departure from the conventional understanding of sparse models. Future research may explore dynamic manifold learning during training, broader applications across neural architectures, and deeper investigations into geometric sparsity's theoretical implications. The novel combination of topology and neural modeling offers promising directions for efficient and interpretable AI development.

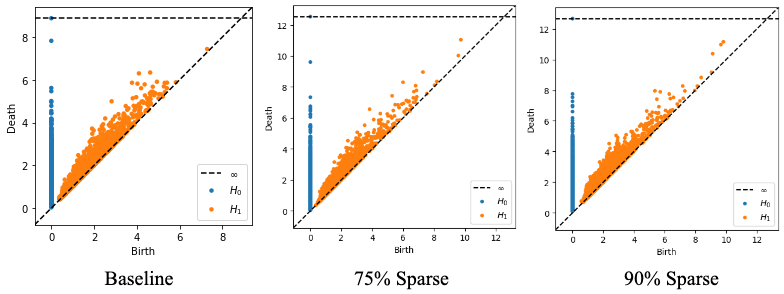
Figure 4: Persistence homology applied to neurons, indicating potential manifold learning insights.