Recurrent neural networks: vanishing and exploding gradients are not the end of the story (2405.21064v2)

Abstract: Recurrent neural networks (RNNs) notoriously struggle to learn long-term memories, primarily due to vanishing and exploding gradients. The recent success of state-space models (SSMs), a subclass of RNNs, to overcome such difficulties challenges our theoretical understanding. In this paper, we delve into the optimization challenges of RNNs and discover that, as the memory of a network increases, changes in its parameters result in increasingly large output variations, making gradient-based learning highly sensitive, even without exploding gradients. Our analysis further reveals the importance of the element-wise recurrence design pattern combined with careful parametrizations in mitigating this effect. This feature is present in SSMs, as well as in other architectures, such as LSTMs. Overall, our insights provide a new explanation for some of the difficulties in gradient-based learning of RNNs and why some architectures perform better than others.

• The paper identifies the 'curse of memory' where stable gradient flows still lead to heightened sensitivity in RNN parameters as memory increases.
• It demonstrates through theoretical analysis that input normalization and eigenvalue reparametrization are critical for mitigating long-term dependency issues in RNNs.
• Empirical validation using teacher-student tasks shows that diagonal architectures with adaptive learning rates significantly improve long-term memory retention over traditional methods.

A Critical Examination of "Recurrent Neural Networks: Vanishing and Exploding Gradients Are Not the End of the Story"

Introduction

The paper "Recurrent Neural Networks: Vanishing and Exploding Gradients Are Not the End of the Story" (2405.21064) presents a nuanced analysis of the challenges faced by Recurrent Neural Networks (RNNs) in learning long-term dependencies. Despite the successes of state-space models (SSMs) in alleviating some of these issues, the paper uncovers an additional layer of complexity, termed the "curse of memory," which persists even when vanishing and exploding gradients are controlled. This essay provides an in-depth exploration of the findings, methodologies, and implications presented in the paper.

Vanishing and Exploding Gradients

The foundational difficulty in training RNNs lies in their tendency to suffer from vanishing and exploding gradients, particularly when processing long sequences. The paper revisits this classic problem and addresses the attempts to remedy it through architectural innovations such as Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU). These innovations have propelled RNNs into practical applications by providing mechanisms for stable gradient flow through gating strategies.

The Curse of Memory

A significant contribution of the paper is the identification and analysis of the "curse of memory." The research posits that as the memory of an RNN increases, the sensitivity of its parameters to small changes is exacerbated, irrespective of the stability of the network dynamics. This sensitivity arises because the recursive application of the update function causes cumulative parameter changes to influence the network's output significantly, even without the presence of exploding gradients.

Figure 1: Optimization of recurrent neural networks gets harder as their memory increases.

Signal Propagation in Linear Diagonal RNNs

The paper investigates signal propagation within linear diagonal RNNs under wide-sense stationary inputs. Using this theoretical framework, the authors derive conditions under which hidden state and gradient magnitudes can remain stable. They demonstrate that careful design patterns, such as input normalization and reparametrization of eigenvalues, are essential for mitigating the adverse effects of the curse of memory.

Mitigating Strategies

The paper explores several strategies to counteract the issues associated with increased memory sensitivity:

1. Input Normalization: By modulating inputs with a scaling factor that considers the network's characteristics and data distribution, it is possible to maintain stable hidden state variances.
2. Eigenvalue Reparametrization: The reparametrization of eigenvalues to prevent their magnitude from approaching one is crucial. This approach aids in averting gradient explosions linked to parameter sensitivity.

The effectiveness of these strategies is demonstrated through theoretical derivations and controlled experiments. The results align closely with empirical observations derived from complex network architectures such as SSMs and gated RNNs like LSTMs.

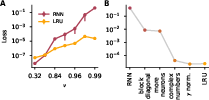
Figure 2: LRUs are better at replicating a teacher's behavior than linear RNNs.

Empirical Validation through Teacher-Student Tasks

Empirical validation is provided through a linear teacher-student task, which serves as a simplified model for understanding how RNNs learn in practice. The results indicate that complex diagonal architectures outperform fully connected RNNs in settings demanding long-term memory retention, attributed to their structural advantages in optimization properties.

The Role of Adaptive Learning Rates

An important insight from the paper is the role of adaptive learning rates, such as those utilized by the Adam optimizer, in compensating for the increased sensitivity of parameters in diagonal RNNs. This adaptive mechanism is less effective in fully connected RNNs due to their entangled parameter updates, highlighting the importance of architecture in optimization efficiency.

Figure 3: Differences in learning abilities between fully connected and complex diagonal linear RNNs are due to a better structure of the loss landscape.

Conclusion

The research enriches the understanding of RNN learning dynamics by introducing the concept of the curse of memory. By identifying and addressing this issue, it opens pathways for enhancing the training of RNNs, particularly through architectural modifications and optimization strategies. The findings have significant implications for the design of efficient and robust sequence models, particularly in applications requiring the integration of long-term dependencies. Future research could further explore the applicability of these findings to larger, more varied datasets and more complex recurrent architectures, potentially bridging the gap between theoretical insights and practical applications in machine learning.