LoRA-XS: Low-Rank Adaptation with Extremely Small Number of Parameters (2405.17604v3)

Abstract: The growth of LLMs underscores the need for parameter-efficient fine-tuning. Despite its popularity, LoRA encounters storage and computational challenges when deploying multiple task- or user-specific modules. To address this, we introduce LoRA-XS, a novel fine-tuning method backed by a theoretical derivation. LoRA-XS drastically reduces trainable parameters by incorporating a small, trainable weight matrix between frozen low-rank matrices derived from the Singular Value Decomposition of pre-trained weights. This design enables LoRA-XS to reduce storage requirements by over 100x in 7B models compared to LoRA. Additionally, unlike other methods, LoRA-XS imposes no lower bound on trainable parameters - it can scale from a single parameter per module to arbitrarily large values, adapting to any storage or computational constraint. Evaluations on GLUE, GSM8K, MATH, and commonsense reasoning benchmarks across different model scales reveal that LoRA-XS consistently outperforms or matches LoRA and VeRA in accuracy, offering unmatched parameter efficiency. Our ablation studies highlight the significance of singular vectors in transformer weights, establishing LoRA-XS as a powerful, storage-efficient solution for scaling and personalizing LLMs.

• The paper introduces LoRA-XS, a method that inserts a small trainable matrix between frozen low-rank matrices from SVD to fine-tune LLMs with minimal parameters.
• It leverages dominant singular vectors for efficient parameter updates, achieving significant memory savings while preserving performance on NLP tasks.
• Experimental results on GLUE and reasoning benchmarks show that LoRA-XS delivers superior or comparable performance to traditional low-rank adaptation techniques.

LoRA-XS: Low-Rank Adaptation with Extremely Small Number of Parameters

This paper presents LoRA-XS, an innovative approach to parameter-efficient fine-tuning of LLMs. The proposed method significantly reduces the number of trainable parameters through a clever use of Singular Value Decomposition (SVD) while maintaining competitive performance across various natural language processing tasks.

Introduction

The expansion of LLMs has enabled significant advancements in NLP, yet their massive scale poses challenges in terms of fine-tuning on specific tasks due to high computational and storage demands. LoRA, a previously established method, addressed these challenges by employing low-rank matrices to adjust the models without affecting inference latencies. However, scaling LoRA across numerous personalized modules leads to impractical storage requirements. LoRA-XS builds upon LoRA, offering a drastic reduction in trainable parameters by introducing a small trainable matrix positioned between frozen low-rank matrices derived from the SVD of pre-trained weights.

Methodology

LoRA-XS leverages the singular vectors from the SVD of the original weight matrix to define its adaptation matrices. These matrices remain fixed during training, and adaptation is achieved through a learnable small matrix R placed between them. This setup decouples the number of trainable parameters from the model's dimensions, allowing flexible resource allocation.

Figure 1: A visual comparison of the LoRA and LoRA-XS techniques. The key innovation of LoRA-XS is its small trainable matrix R, positioned between two frozen low-rank matrices derived from the truncated SVD of pre-trained weights.

Theoretical Foundations

LoRA-XS relies on aligning updates to the dominant singular directions of weights, proven to enhance adaptation efficiency. Unlike traditional methodologies requiring fixed amounts of additional parameters, LoRA-XS tailors itself to memory constraints, ranging from minimal to extensive parameter usage without compromising the core model architecture.

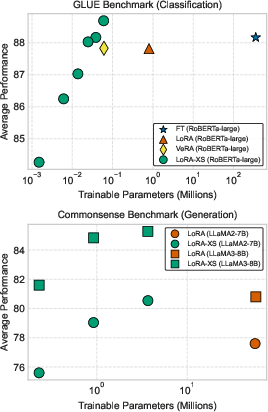
Figure 2: Average performance for a given number of trainable parameters across different adaptation methods and model scales. LoRA-XS consistently outperforms other methods in both parameter efficiency and average performance.

Experimental Results

Evaluations were performed using the GLUE benchmark along with commonsense and mathematical reasoning datasets. LoRA-XS achieved superior or comparable results to LoRA and VeRA across diverse tasks and model sizes. Notably, LoRA-XS surpassed baseline methods with significantly fewer parameters.

These results underscore LoRA-XS's capability for practical deployment in environments where memory constraints are critical, such as embedded systems or large-scale server deployments catering to multiple users.

Ablation Studies

The paper presents comprehensive ablation studies assessing the importance of singular vectors in transformer weights. The analysis confirmed that focusing on top singular vectors—those associated with the largest singular values—yields optimal performance, validating the design choices inherent in LoRA-XS.

Conclusion

LoRA-XS introduces a paradigm shift in parameter-efficient tuning, leveraging theoretical insights to offer remarkable memory savings while maintaining strong task performance. This balance of efficiency and adaptability positions LoRA-XS as a potent tool for scaling and personalizing LLMs, synergistically with other memory-saving techniques like pruning or quantization.

Future research directions could explore integrating LoRA-XS into dynamic rank adaptation strategies or further optimizing its integration with quantized models, offering even broader applicability across computationally constrained environments.

By refining LLM adaptation through low-dimensional updates informed by pre-trained weight structures, LoRA-XS exemplifies an impactful advancement in efficient model tuning.