Base of RoPE Bounds Context Length (2405.14591v1)

Abstract: Position embedding is a core component of current LLMs. Rotary position embedding (RoPE), a technique that encodes the position information with a rotation matrix, has been the de facto choice for position embedding in many LLMs, such as the Llama series. RoPE has been further utilized to extend long context capability, which is roughly based on adjusting the \textit{base} parameter of RoPE to mitigate out-of-distribution (OOD) problems in position embedding. However, in this paper, we find that LLMs may obtain a superficial long-context ability based on the OOD theory. We revisit the role of RoPE in LLMs and propose a novel property of long-term decay, we derive that the \textit{base of RoPE bounds context length}: there is an absolute lower bound for the base value to obtain certain context length capability. Our work reveals the relationship between context length and RoPE base both theoretically and empirically, which may shed light on future long context training.

• The paper introduces a lower-bound threshold for RoPE's base, ensuring effective long-context handling in LLMs.
• It details the long-term decay property of RoPE, which diminishes token discrimination as relative distances increase.
• Experimental results show that insufficient base settings yield low perplexity scores yet fail to achieve genuine long-sequence comprehension.

Base of RoPE Bounds Context Length

Introduction

The use of positional embeddings remains a crucial aspect within LLMs, where the Rotary Position Embedding (RoPE) has become a widely adopted mechanism. Despite its popularity in models like Llama, the link between RoPE's base value and the context length that an LLM can efficiently handle has not been comprehensively explored. In this exploration, we discuss the theory that an absolute lower-bound base value exists for RoPE to achieve a certain context length capability. This theoretical insight challenges the common assumption about the effectiveness of merely adjusting the base as a means to mitigate out-of-distribution (OOD) issues. Ultimately, the interplay between context length and RoPE base informs the long context training strategy for future LLMs.

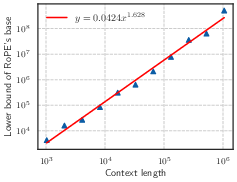
Figure 1: Context length and its corresponding lower bound of RoPE's base value.

RoPE and Long Context Extrapolation

RoPE leverages a rotation matrix to encode positional information, facilitating the extension of context lengths without excessive training. Contrary to the expectation that simply increasing the base value will ensure sufficient extrapolation to new context lengths, it's shown that a profound understanding of RoPE's theoretical underpinnings is essential for effective long-context capabilities.

Debates revolve around the superficiality of long-context capability claims when relying on OOD approaches to RoPE. It emerges that while empirical evidence suggests a larger base allows for superior performance on extended context lengths, the derivation of a fundamental lower bound is needed to substantiate these claims theoretically.

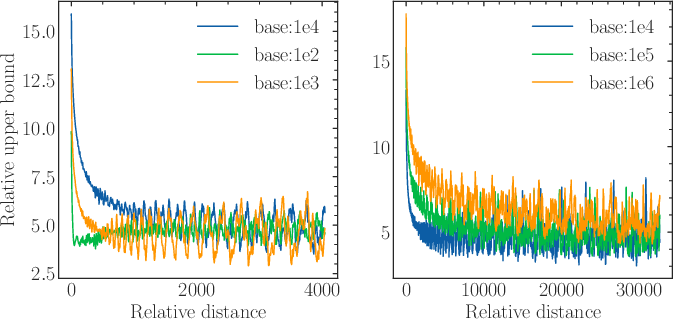
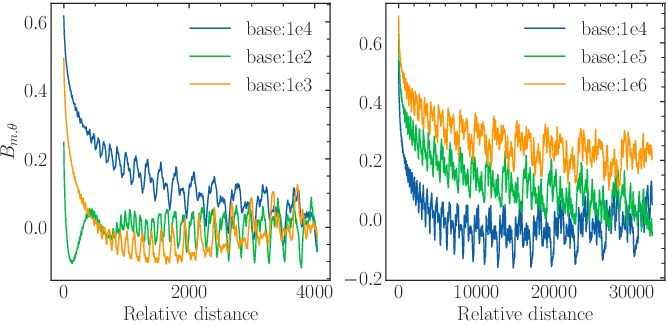
Figure 2: The upper bound of attention score with respect to the relative distance.

Theoretical Underpinnings of RoPE's Base

The main theoretical contribution lies in highlighting the long-term decay property of RoPE, which diminishes the model's power to distinguish between similar tokens as the relative distance increases. This decay is formalized as:

$B_{m,\theta} = \sum_{i=0}^{d/2-1}\cos(m\theta_i)$

This function quantifies the relative distance's effect on attention, stipulating that $B_{m,\theta}$ should be greater than zero for practical discrimination. Inserting these into context-bound calculations yields a base threshold for certain context lengths. Empirical results show models with bases under this threshold maintain low perplexity, yet exhibit reduced proficiency with longer sequences.

Experimental Validation

Experiments validated the derived lower bound of RoPE's base. Through fine-tuning Llamas and Baichuan2 models on various context lengths, it was confirmed that when the RoPE's base is below the critical threshold, extrapolation fails past a certain point—manifested as poor retrieval accuracy despite low perplexity.

• Base setting experiments demonstrated improved long-context analytics when adjusting RoPE bases above the theoretical threshold.
• Superficial long-context capability was scrutinized by revealing how models with insufficient base settings yield low perplexity scores without genuine extensive sequential comprehension.

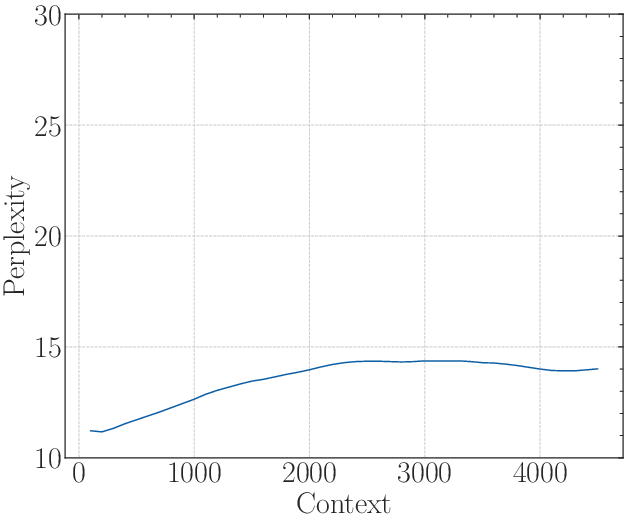
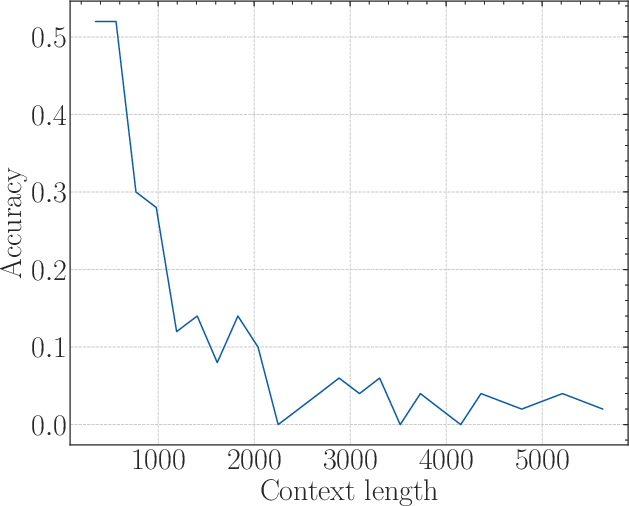
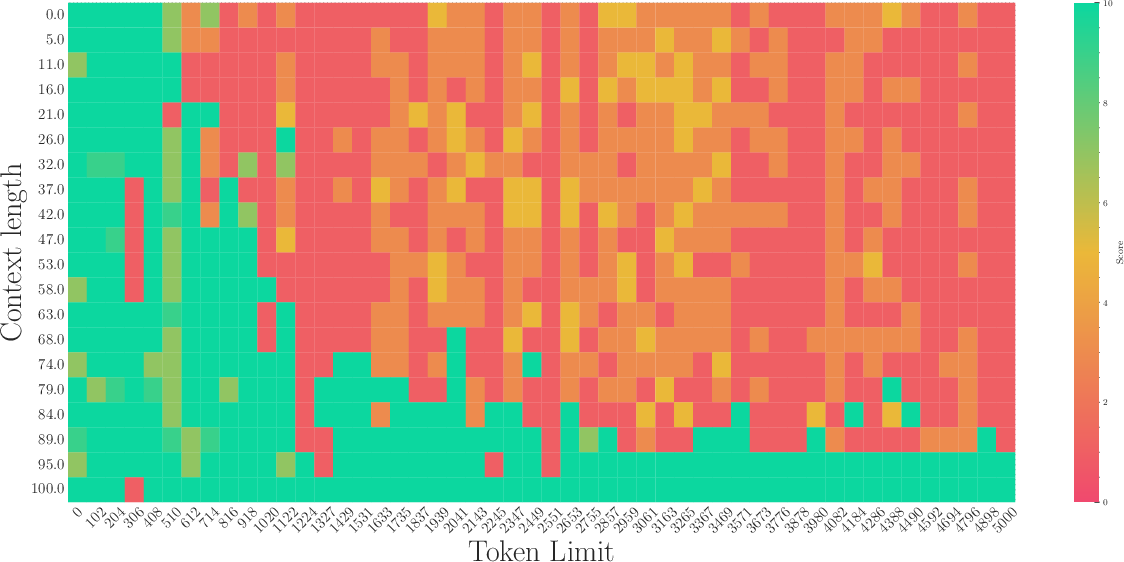
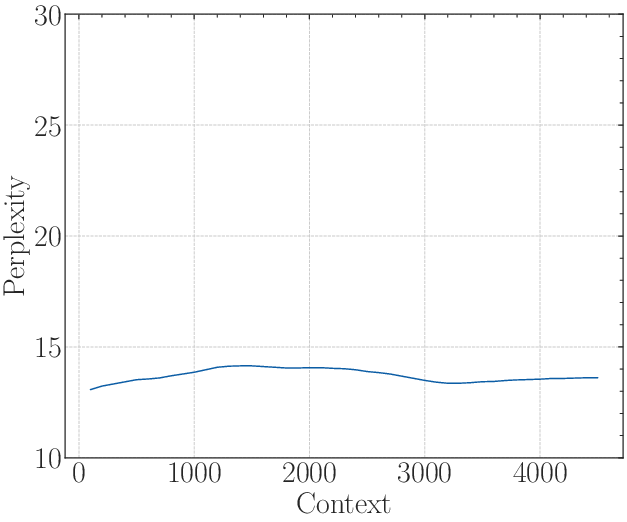
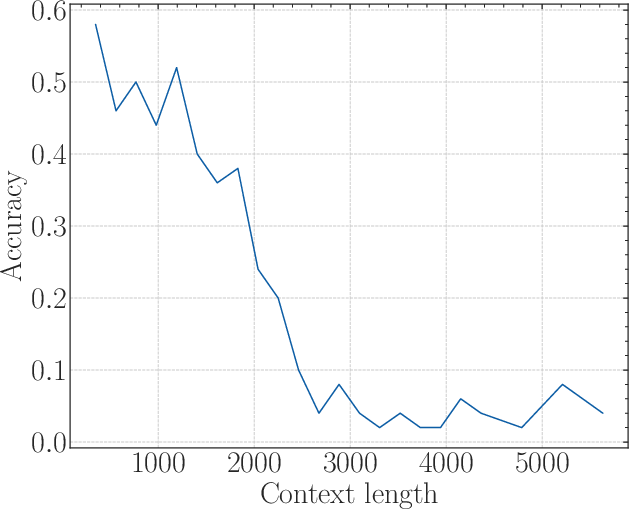
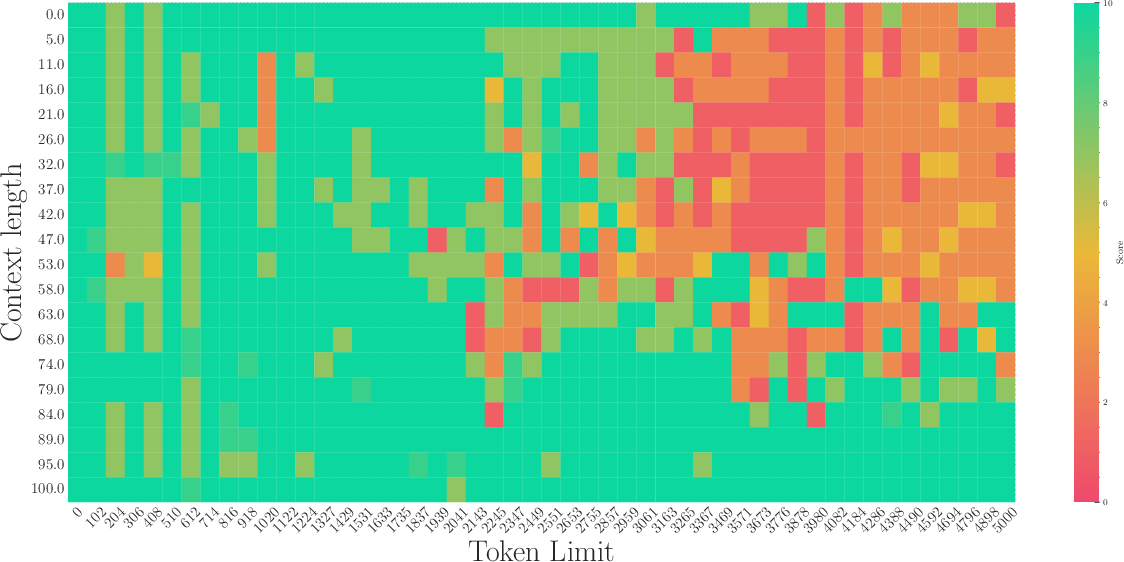
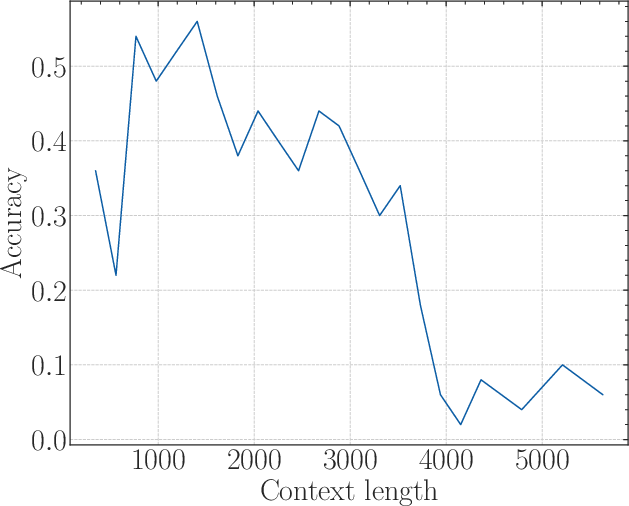
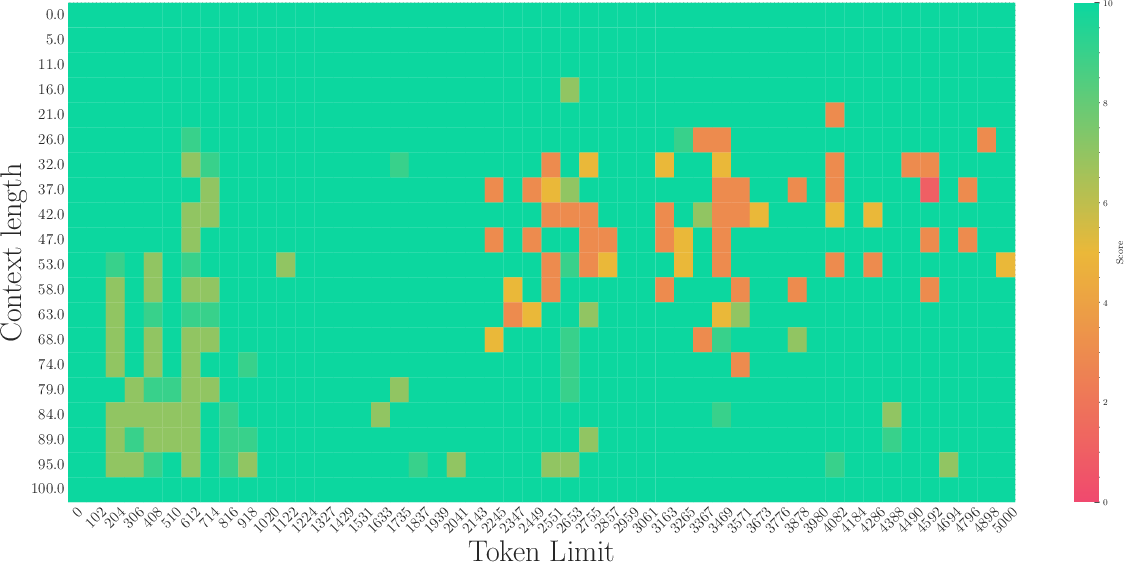
Figure 3: The first row: the results of a 2B model training from scratch with base=1e2. The second row: The results of fine-tuning the 2B model with base=1e4. The third row: The results of fine-tuning the 2B model with base=1e6.

Practical Implications and Future Directions

The findings challenge the prevailing methods in LLM development by advocating for a reevaluation of base adjustments in RoPE, stressing that out-of-distribution rotation angles inadequately forecast long-context processing. The theoretical lower bound can guide future improvements in LLM designs, ensuring models are primed for authentic large-context comprehension without relying solely on perplexity as a metric.

Future work could investigate the existence of an upper bound for RoPE's base, further elucidating the role of RoPE bases in pre-training contexts, and exploring new techniques to dynamically adjust RoPE parameters to optimize both memory efficiency and computational throughput.

Conclusion

This framework reshapes understanding of RoPE within LLMs, emphasizing a precise theoretical approach to the base and context length relationship. By aligning empirical practices with robust theoretical foundations, we derive substantial insights for designing LLMs equipped to tackle long-context application scenarios effectively.

Through this synthesis of theory and empirical evidence, this paper outlines the requisite trajectory for advancing long-context modeling beyond current limitations, providing a bedrock for future explorations in this domain.