Bridging discrete and continuous state spaces: Exploring the Ehrenfest process in time-continuous diffusion models (2405.03549v1)

Abstract: Generative modeling via stochastic processes has led to remarkable empirical results as well as to recent advances in their theoretical understanding. In principle, both space and time of the processes can be discrete or continuous. In this work, we study time-continuous Markov jump processes on discrete state spaces and investigate their correspondence to state-continuous diffusion processes given by SDEs. In particular, we revisit the $\textit{Ehrenfest process}$, which converges to an Ornstein-Uhlenbeck process in the infinite state space limit. Likewise, we can show that the time-reversal of the Ehrenfest process converges to the time-reversed Ornstein-Uhlenbeck process. This observation bridges discrete and continuous state spaces and allows to carry over methods from one to the respective other setting. Additionally, we suggest an algorithm for training the time-reversal of Markov jump processes which relies on conditional expectations and can thus be directly related to denoising score matching. We demonstrate our methods in multiple convincing numerical experiments.

• The paper establishes a connection between discrete Markov jump processes and continuous diffusion models via the Ehrenfest-OU process convergence.
• It leverages conditional expectations and τ-leaping to compute reverse process rates, enabling efficient training on datasets like MNIST and CIFAR-10.
• The work links reverse-time dynamics with score-based generative modeling, fostering innovations in hybrid discrete-continuous approaches.

Bridging Discrete and Continuous State Spaces in Diffusion Models

Introduction

The paper "Bridging discrete and continuous state spaces: Exploring the Ehrenfest process in time-continuous diffusion models" focuses on the interplay between discrete and continuous state spaces in the domain of generative models. It examines time-continuous Markov jump processes on discrete state spaces and their connection to state-continuous diffusion processes described by stochastic differential equations (SDEs). A centerpiece of this investigation is the Ehrenfest process, which transitions into an Ornstein-Uhlenbeck process in the limit of infinite state space, establishing a link between these modeling paradigms.

Time-Reversed Markov Jump Processes

The paper investigates time-reversed Markov jump processes, which transition discretely over time in a discrete state space. The emphasis on reverse-time processes is grounded in their application to generative modeling, where diffusion mechanisms drive data towards a known equilibrium, and reversing this process recovers the desired data distribution.

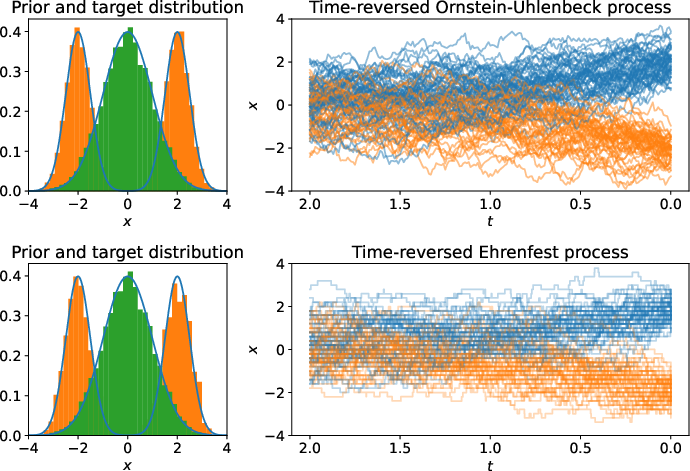
Figure 1: We display two time-reversed processes from $t = 2$ to $t = 0$ that transport a standard Gaussian to a multimodal Gaussian mixture model, showcasing the diffusion in continuous and discrete spaces.

To compute the rates for these time-reversed processes, the paper provides a formula that depends on conditional expectations and transition probabilities. This formula directly relates to denoising score matching, an essential approach in score-based generative models.

The Ehrenfest Process

The Ehrenfest process, originally introduced in statistical mechanics, demonstrates properties in a discrete setting analogous to the continuous-state Ornstein-Uhlenbeck process. In the discrete domain, the process involves birth-death transitions, which, when scaled appropriately, converge to a state-continuous process in the infinite state space limit.

Remarkable in this context is the possibility to sample directly from the transition probability without simulating the entire process, leveraging binomial random variables. This characteristic significantly reduces computational overhead, allowing efficient training and simulation.

Figure 2: Histograms of samples from the time-reversed scaled Ehrenfest process highlight the conditional expectation's role in guiding the reverse dynamics.

Connection to Score-Based Generative Modeling

One of the paper's significant contributions is establishing a profound connection between the time-reversal of the Ehrenfest process and score-based generative modeling. By analyzing the jump moments and their convergence properties, the paper shows that reverse processes of Markov jump dynamics can approximate the score function—a key component in continuous diffusion models.

This connection allows transferring insights and techniques between discrete and continuous settings, fostering a deeper understanding of generative processes and enabling novel algorithm designs.

Computational Approach

The paper details the computational strategies employed for training and sampling these processes. It incorporates conditional expectations to learn reverse process rates and employs $\tau$-leaping for efficient sampling. These methods are crucial for scaling the approach to high-dimensional data, such as images, and are validated through experiments on standard datasets like MNIST and CIFAR-10.

Figure 3: MNIST and CIFAR-10 samples illustrate the model's ability to generate coherent and high-quality data resembling real-world images.

Experimental Validation

The empirical results demonstrate the efficacy of the proposed methods. Models trained with the Ehrenfest process achieve compelling performance on MNIST and CIFAR-10, matching or surpassing existing methods. The experiments underscore the process's ability to bridge discrete and continuous domains effectively, providing competitive generation quality with state-of-the-art models.

Conclusion

By extending the theoretical and practical understanding of how discrete and continuous state spaces can be unified in diffusion models, this research opens avenues for further exploration in generative modeling. Its insights provide a robust framework for developing models that leverage the strengths of both discrete and continuous domains, with promising implications for various data types and applications.

In summary, this paper lays the groundwork for future developments in hybrid generative processes, enabling richer, more flexible models that can adeptly handle complex datasets across different modalities.