KAN: Kolmogorov-Arnold Networks (2404.19756v4)

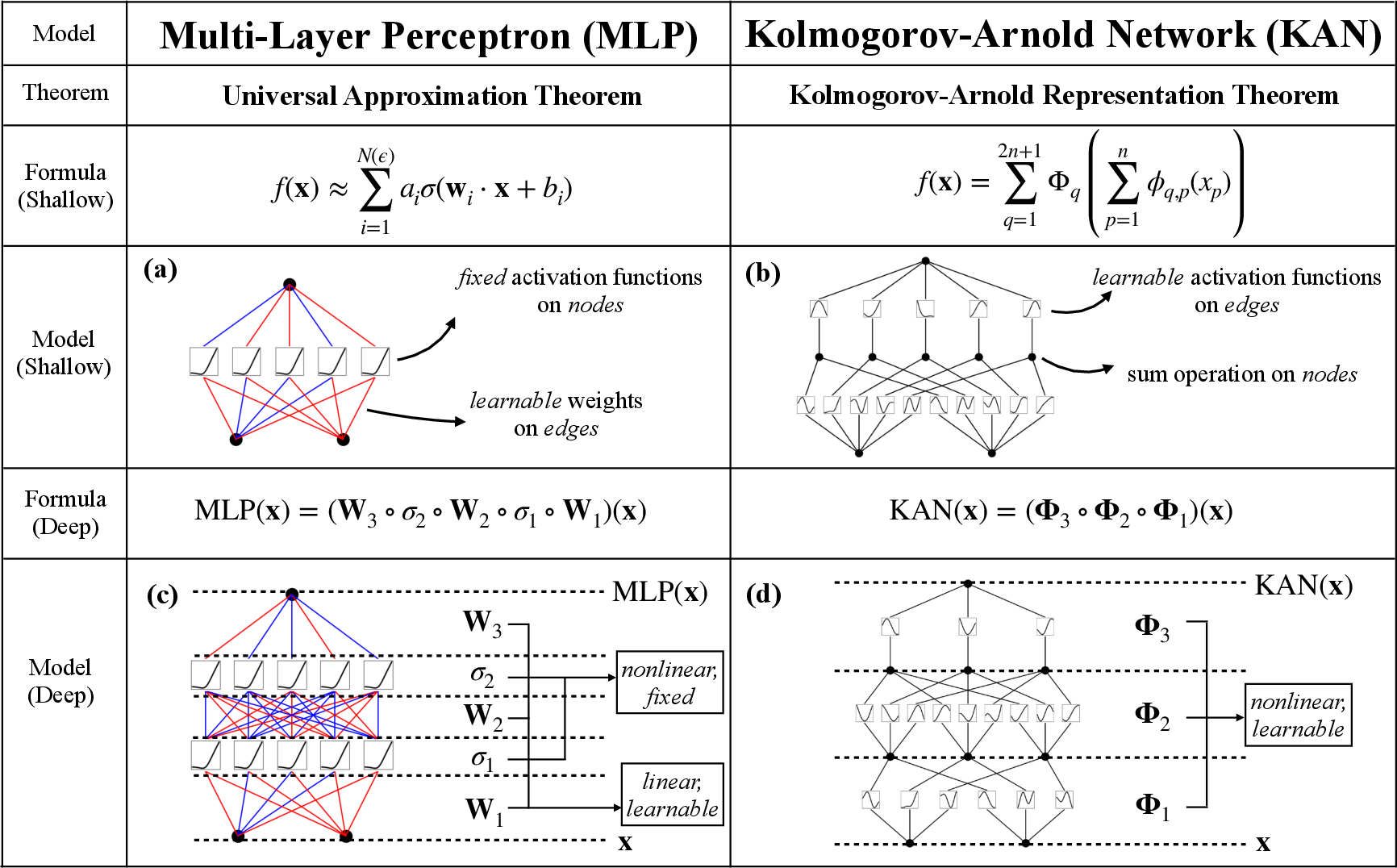
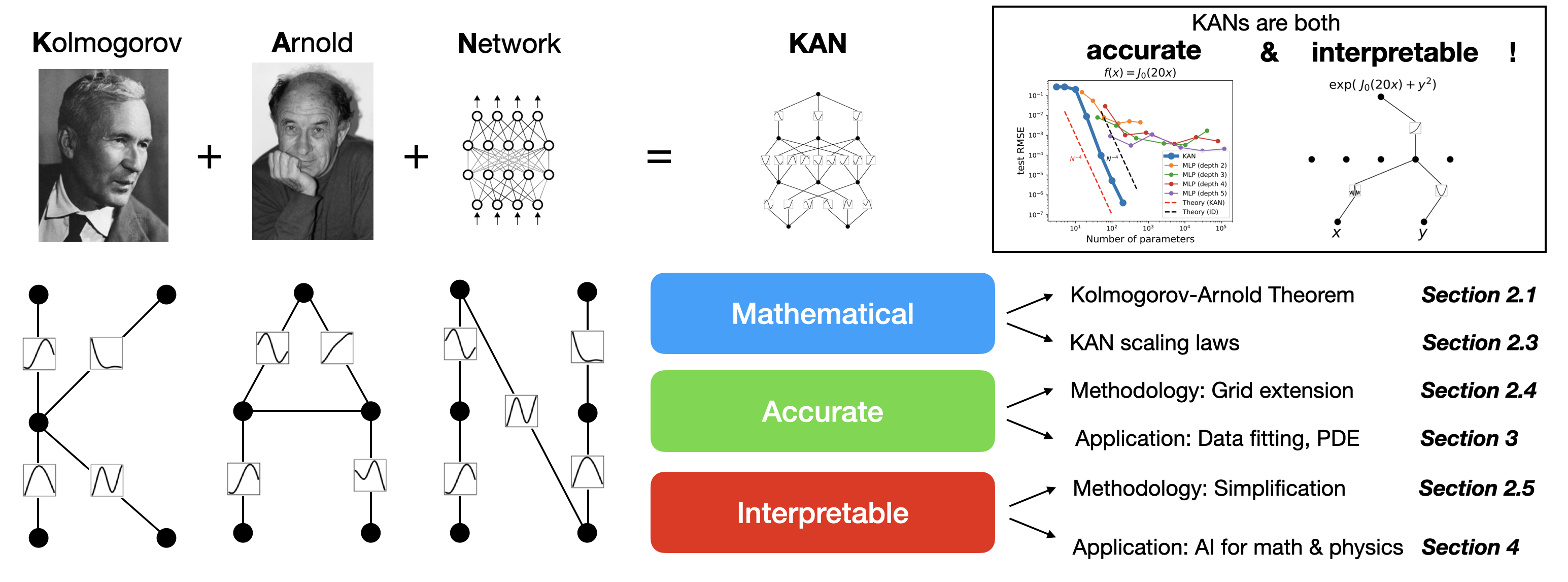
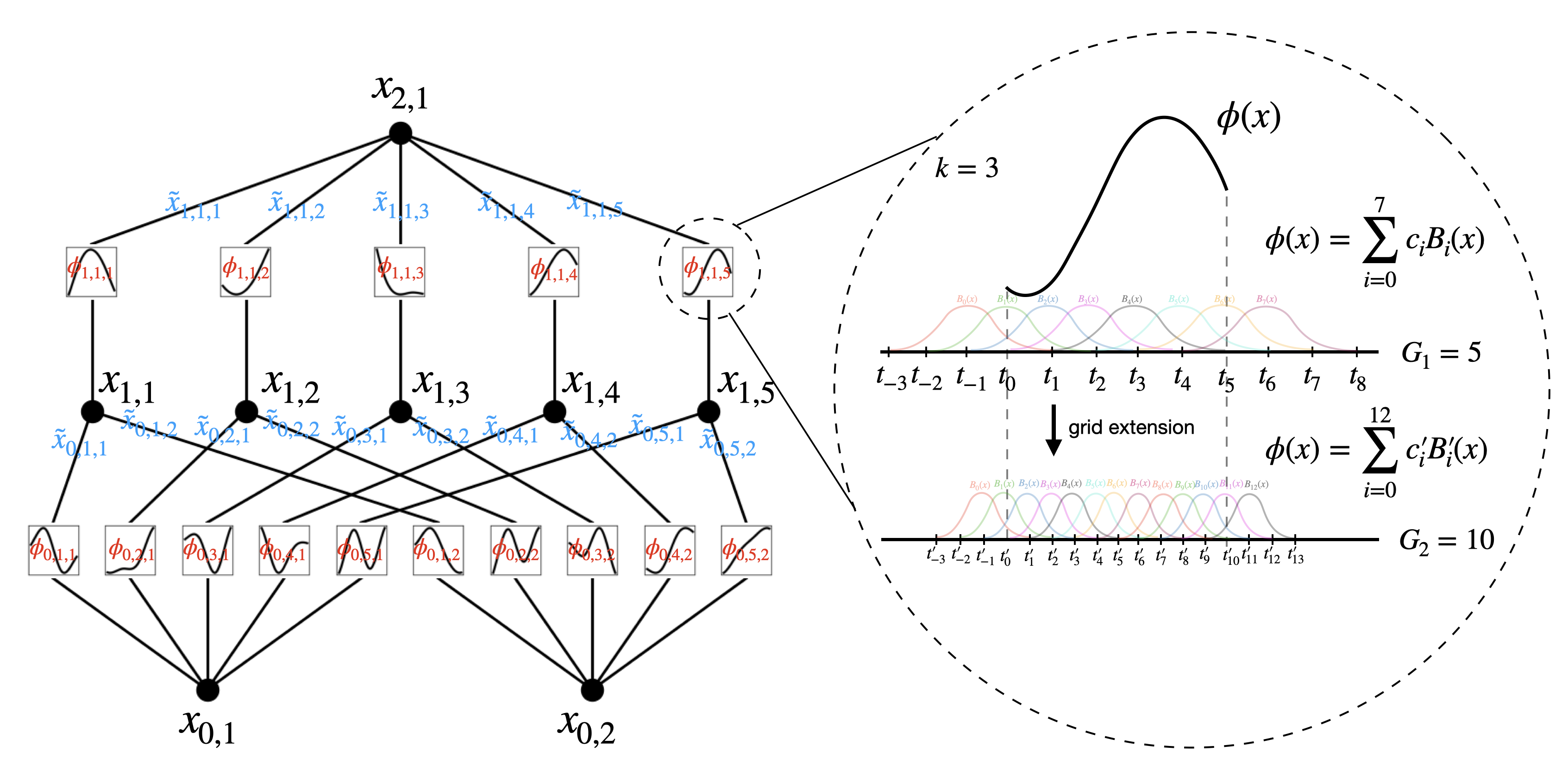
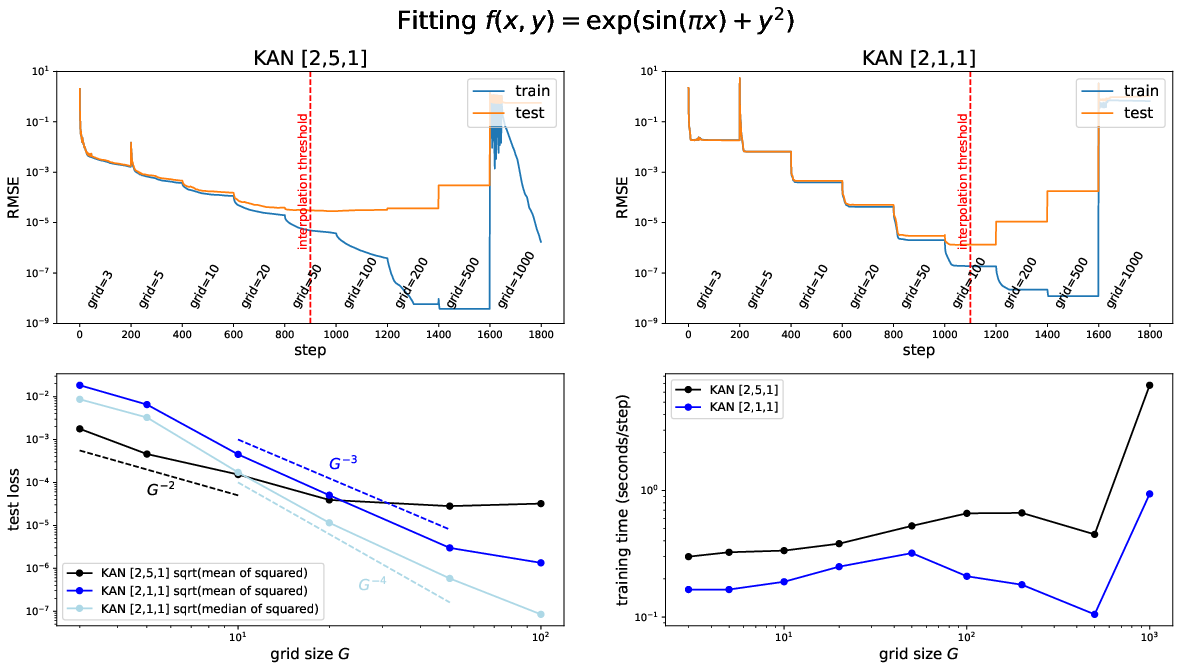
Abstract: Inspired by the Kolmogorov-Arnold representation theorem, we propose Kolmogorov-Arnold Networks (KANs) as promising alternatives to Multi-Layer Perceptrons (MLPs). While MLPs have fixed activation functions on nodes ("neurons"), KANs have learnable activation functions on edges ("weights"). KANs have no linear weights at all -- every weight parameter is replaced by a univariate function parametrized as a spline. We show that this seemingly simple change makes KANs outperform MLPs in terms of accuracy and interpretability. For accuracy, much smaller KANs can achieve comparable or better accuracy than much larger MLPs in data fitting and PDE solving. Theoretically and empirically, KANs possess faster neural scaling laws than MLPs. For interpretability, KANs can be intuitively visualized and can easily interact with human users. Through two examples in mathematics and physics, KANs are shown to be useful collaborators helping scientists (re)discover mathematical and physical laws. In summary, KANs are promising alternatives for MLPs, opening opportunities for further improving today's deep learning models which rely heavily on MLPs.

• The paper introduces KANs, which replace fixed neuron activations with learnable spline-based functions on edges, leading to improved accuracy and interpretability.
• It presents technical innovations such as dynamic grid updates, residual activation functions, and sparsification to optimize training and simplify network structure.
• Experimental results show KANs outperform traditional MLPs in tasks ranging from PDE solutions to symbolic regression, achieving efficient scaling and robust function approximation.

Kolmogorov-Arnold Networks (KANs) are proposed as a promising alternative to Multi-Layer Perceptrons (MLPs), drawing inspiration from the Kolmogorov-Arnold representation theorem. While traditional MLPs utilize fixed activation functions on nodes (neurons), KANs introduce learnable activation functions on the edges (weights). This means KANs have no linear weight matrices; instead, each weight parameter is replaced by a univariate function parameterized as a spline. The nodes in a KAN simply sum the incoming signals. This architectural change is shown to lead to improved accuracy and interpretability on small-scale AI + Science tasks.

The Kolmogorov-Arnold representation theorem states that any continuous function $f$ of $n$ variables on a bounded domain can be written as a finite composition involving only univariate functions and the binary operation of addition: $$f(x_1, \dots, x_n) = \sum_{q=1}^{2n+1} \Phi_q \left(\sum_{p=1}^n \phi_{q,p}(x_p)\right)$$. While the original theorem implies a shallow, specific structure (depth-2, width $2n+1$), early attempts to build neural networks directly from this theorem were hindered by the requirement for potentially non-smooth or fractal-like univariate functions and the limited applicability of the shallow structure. The paper generalizes this idea to arbitrary widths and depths, framing a KAN as a composition of "KAN layers."

A KAN layer with $n_{in}$ inputs and $n_{out}$ outputs is defined by a matrix of univariate functions ${\mathbf\Phi} = \{\phi_{q,p}\}$, where $p=1,\dots,n_{in}$ and $q=1,\dots,n_{out}$. The forward pass through a layer is given by $x_{l+1,j} = \sum_{i=1}^{n_l} \phi_{l,j,i}(x_{l,i})$, where $x_{l,i}$ is the activation of neuron $(l,i)$ and $\phi_{l,j,i}$ is the learnable activation function on the edge connecting $(l,i)$ to $(l+1,j)$. A deep KAN is formed by stacking these layers.

Key implementation details are crucial for making KANs trainable:

1. Residual activation functions: Each activation function $\phi(x)$ is parameterized as a sum of a fixed basis function $b(x)$ (like SiLU) and a spline function: $\phi(x) = w_b b(x) + w_s \text{spline}(x)$. The spline part is a linear combination of B-spline basis functions, $\sum c_i B_i(x)$, where $c_i$ are trainable coefficients. $w_b$ and $w_s$ are trainable scaling factors.
2. Initialization: Spline coefficients $c_i$ are initialized near zero so $\text{spline}(x) \approx 0$ initially. $w_s$ is initialized to 1, and $w_b$ is initialized like linear weights in MLPs (e.g., Xavier initialization). This ensures the network behaves like an MLP with residual connections initially.
3. Dynamic Grid Update: Spline grids are updated during training based on the distribution of input activations to handle evolving activation ranges.

The parameter count for a KAN with depth $L$, width $N$, spline order $k$, and $G$ intervals is $O(N^2 L G)$. While this appears larger than an MLP's $O(N^2 L)$, KANs often achieve better performance with much smaller widths and depths, resulting in fewer total parameters.

A theoretical analysis shows that if a function admits a smooth Kolmogorov-Arnold representation, a KAN with finite grid size $G$ can approximate the function with an error bound of $O(G^{-k-1+m})$ in $C^m$ norm (Theorem 2.1). This bound is independent of the input dimension $n$, suggesting that KANs can potentially beat the curse of dimensionality (COD) for functions with compositional structure, unlike standard approximation theories for MLPs which predict errors scaling with $1/d$. This leads to a theoretical neural scaling law of $\ell \propto N^{-(k+1)}$ for KANs, which is faster than typical MLP scaling laws ($\alpha = (k+1)/d$ or $\alpha=(k+1)/2$).

A practical technique to improve KAN accuracy is grid extension. Since splines can approximate functions more accurately with finer grids, a trained KAN can be extended to a higher-resolution KAN by fitting the old coarse-grained splines with new fine-grained ones. This allows improving accuracy without retraining from scratch, unlike scaling up MLPs. Experiments show staircase-like loss curves where loss drops significantly after each grid extension. Smaller KANs tend to generalize better and tolerate larger grid sizes before overfitting.

KANs emphasize interpretability. Techniques are developed to simplify trained networks:

1. Sparsification: L1 regularization on the magnitude of activation functions and an additional entropy regularization encourage sparsity among activation functions. The total loss is $$\ell_{\rm total} = \ell_{\rm pred} + \lambda (\mu_1 \sum_l |\mathbf{\Phi}_l|_1 + \mu_2 \sum_l S(\mathbf{\Phi}_l))$$, where $|\mathbf{\Phi}_l|_1$ is the sum of L1 norms of activations in layer $l$, and $S(\mathbf{\Phi}_l)$ is an entropy term.
2. Visualization: Activation functions are visualized with transparency proportional to their magnitude, highlighting important connections.
3. Pruning: Nodes are pruned based on the maximum L1 norm of their incoming and outgoing connections.
4. Symbolification: Numerical activation functions can be snapped to symbolic forms (e.g., sin, exp, log). This is done by fitting affine parameters $(a,b,c,d)$ such that the numerical output $y$ matches $c f(ax+b)+d$ for a potential symbolic function $f$. Functions like fix_symbolic and suggest_symbolic facilitate this.

An interactive workflow using these techniques allows human users to collaborate with KANs to discover symbolic formulas. Starting with a larger KAN, training with sparsification, pruning away unimportant neurons, visually inspecting activation functions, manually fixing them to guessed symbolic forms, and retraining affine parameters can lead to discovering the underlying symbolic expression, as demonstrated with the example $f(x,y) = \exp(\sin(\pi x)+y^2)$. This iterative process offers more transparency and debuggability compared to traditional symbolic regression methods.

Experimental results confirm KANs' practical advantages.

• On toy datasets with known compositional structures, KANs exhibit neural scaling laws much closer to the theoretically predicted $\ell \propto N^{-4}$ than MLPs, which scale slower and plateau quickly.
• Fitting special functions (multivariate functions common in science like Bessel or Legendre functions), KANs consistently outperform MLPs on Pareto frontiers comparing parameter count and RMSE. KANs can find surprisingly compact representations for these functions.
• On the Feynman dataset (real-world physics equations), KANs achieve comparable or better accuracy than MLPs with fewer parameters. Auto-pruned KAN shapes are often smaller than human-constructed ones, hinting at potentially more efficient representations.
• For solving Partial Differential Equations (PDEs) using Physics-Informed Neural Networks (PINNs), a small KAN can achieve significantly higher accuracy and parameter efficiency than a much larger MLP on a Poisson equation example.
• In preliminary experiments on continual learning, the locality of spline basis functions in KANs helps prevent catastrophic forgetting in a toy 1D regression task, allowing the network to learn new tasks without degrading performance on previously learned ones.

Beyond supervised tasks, KANs can be used for unsupervised learning to discover implicit relations $f(x_1, \dots, x_d) \approx 0$ among variables. By training a KAN to classify real data vs. permuted (corrupted) data and structuring the last layer with a Gaussian activation centered at zero, the network implicitly learns $f \approx 0$ for real data. This method successfully rediscovers known mathematical relations in the Knot Theory dataset (dependence of signature on meridinal/longitudinal translations, the relation $V=\mu_r\lambda$, and a relation between short geodesic and injectivity radius).

In condensed matter physics, KANs are applied to extract mobility edges in quasiperiodic models. For simpler models like the Mosaic Model and Generalized Andre-Aubry Model, KANs, guided by user assumptions, can accurately extract the mobility edge functions or formulas close to theoretical ground truths. For the more complex Modified Andre-Aubry Model, a human-KAN collaborative approach involving initial training, pruning, manual symbolic snapping based on visual inspection, and testing different symbolic hypotheses (e.g., testing $\cosh(p)$ dependence) demonstrates how scientists can use KANs as a flexible tool to trade off simplicity and accuracy in discovered formulas, facilitating scientific discovery.

Potential limitations include the need for a deeper mathematical understanding of KANs beyond the original KAT, algorithmic aspects like optimizing training efficiency (KANs are currently slower than MLPs, especially due to spline evaluation overhead), and exploring hybrid architectures combining KANs and MLPs or using different basis functions. However, the paper argues that KANs' interpretability and potential for better accuracy make them a valuable tool for AI + Science, serving as a "LLM" of functions for human-AI collaboration.

The decision to use KANs over MLPs depends on the priorities: if training speed is paramount, MLPs might be preferred. However, if accuracy and interpretability are key, especially for small-to-medium scale science and engineering problems where understanding the underlying relationships is important, KANs offer significant advantages despite slower training.