NeurCADRecon: Neural Representation for Reconstructing CAD Surfaces by Enforcing Zero Gaussian Curvature (2404.13420v1)

Abstract: Despite recent advances in reconstructing an organic model with the neural signed distance function (SDF), the high-fidelity reconstruction of a CAD model directly from low-quality unoriented point clouds remains a significant challenge. In this paper, we address this challenge based on the prior observation that the surface of a CAD model is generally composed of piecewise surface patches, each approximately developable even around the feature line. Our approach, named NeurCADRecon, is self-supervised, and its loss includes a developability term to encourage the Gaussian curvature toward 0 while ensuring fidelity to the input points. Noticing that the Gaussian curvature is non-zero at tip points, we introduce a double-trough curve to tolerate the existence of these tip points. Furthermore, we develop a dynamic sampling strategy to deal with situations where the given points are incomplete or too sparse. Since our resulting neural SDFs can clearly manifest sharp feature points/lines, one can easily extract the feature-aligned triangle mesh from the SDF and then decompose it into smooth surface patches, greatly reducing the difficulty of recovering the parametric CAD design. A comprehensive comparison with existing state-of-the-art methods shows the significant advantage of our approach in reconstructing faithful CAD shapes.

• The paper introduces NeurCADRecon, a self-supervised method that enforces zero Gaussian curvature to achieve high-fidelity reconstruction from noisy point clouds.
• It employs a dynamic sampling strategy to address sparse data and precisely recover sharp feature points and parametric CAD details.
• Experimental results on ABC, Fusion Gallery, and DeepCAD datasets showcase its superiority over traditional techniques for CAD surface recovery.

NeurCADRecon: Neural Representation for Reconstructing CAD Surfaces by Enforcing Zero Gaussian Curvature

Abstract

"NeurCADRecon: Neural Representation for Reconstructing CAD Surfaces by Enforcing Zero Gaussian Curvature" (2404.13420) introduces a self-supervised learning method aimed at reconstructing Computer-Aided Design (CAD) models from unoriented point clouds, addressing the challenge of high-fidelity reconstruction directly from noisy inputs. The paper proposes the novel approach of encouraging the Gaussian curvature of the surface toward zero, leveraging the developability of CAD model surfaces which are typically composed of piecewise smooth patches. To address the presence of non-zero Gaussian curvature at tip points, the authors utilize a double-trough curve for tolerance and introduce a dynamic sampling strategy to handle incomplete or sparse input data. Their method outperforms existing techniques in reconstructing sharp feature points and lines, facilitating the recovery of parametric CAD designs.

Introduction

Reconstructing CAD models from low-quality, unoriented point clouds is a fundamental task in both academic and industrial settings. Despite significant advances in the reconstruction of organic models, CAD models pose unique challenges due to their characteristic sharp feature points and lines. The surface of CAD models is typically composed of smooth, developable surface patches. The paper presents NeurCADRecon, which optimizes the neural signed distance function (SDF) with a loss that encourages zero Gaussian curvature, benefiting from the inherent developability of CAD surfaces.

Methodology

NeurCADRecon employs a self-supervised neural network to estimate the signed distance function by encouraging the Gaussian curvature toward zero, enabling the extraction of a feature-aligned mesh. The loss function integrates previously established conditions such as the Dirichlet and Eikonal conditions, but crucially adds a developability term focused on minimizing the Gaussian curvature across the surface.

Gaussian Curvature Constraint

The Gaussian curvature is vital for accurately encoding the CAD surface properties. By focusing on developability, as characterized by zero Gaussian curvature, NeurCADRecon effectively captures the essence of CAD surface geometry. This approach improves over traditional rank constraints of Hessians due to enhanced numerical stability and the ability to handle scenarios with non-zero curvature at tip points.

Dynamic Sampling

To address incomplete or sparse sampling in the input point cloud, NeurCADRecon incorporates dynamic sampling. This strategy projects additional sample points onto the surface, allowing the model to continuously adjust the loss measurements, thereby improving the quality of surface reconstruction even in data-sparse areas.

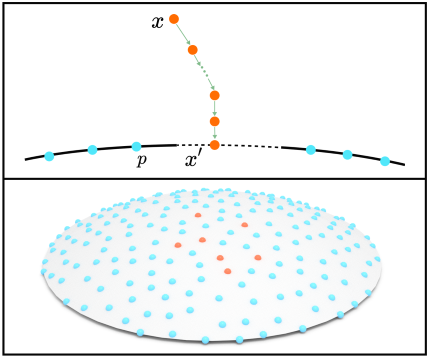
Figure 1: We project a point onto the surface based on Eq.~(\ref{eq:proj.

Experiments

Extensive comparisons on several public datasets demonstrate that NeurCADRecon consistently surpasses state-of-the-art methods in reconstructing CAD shapes with high fidelity.

Comparative Analysis

Results on datasets like ABC, Fusion Gallery, and DeepCAD confirm the robustness of NeurCADRecon in recovering accurate surface geometries, outperforming baseline methods across metrics such as Normal Consistency, Chamfer Distance, and F1-Score. Particularly noteworthy is its superior performance in handling noisy and sparse data, two common issues in real-world CAD applications.

Figure 2: A gallery of reconstruction results by our NeurCADRecon. The central idea is to encourage the Gaussian curvature toward 0 while ensuring fidelity to the input points.

Applications

Beyond mere reconstruction, NeurCADRecon facilitates secondary design tasks, such as resizing CAD models by decomposing the reconstructed mesh into smooth surface patches along sharp feature lines. This significantly reduces the complexity involved in recovering the parametric CAD design, enabling practical applications in design and manufacturing processes.

Conclusion

NeurCADRecon effectively reconstructs high-fidelity CAD models from unoriented point clouds, with capabilities enhanced by enforcing developability through zero Gaussian curvature. Its dynamic sampling strategy and robust handling of data imperfections position it as a notable advance in CAD surface reconstruction, offering tangible benefits for both theoretical exploration and practical application in the field.