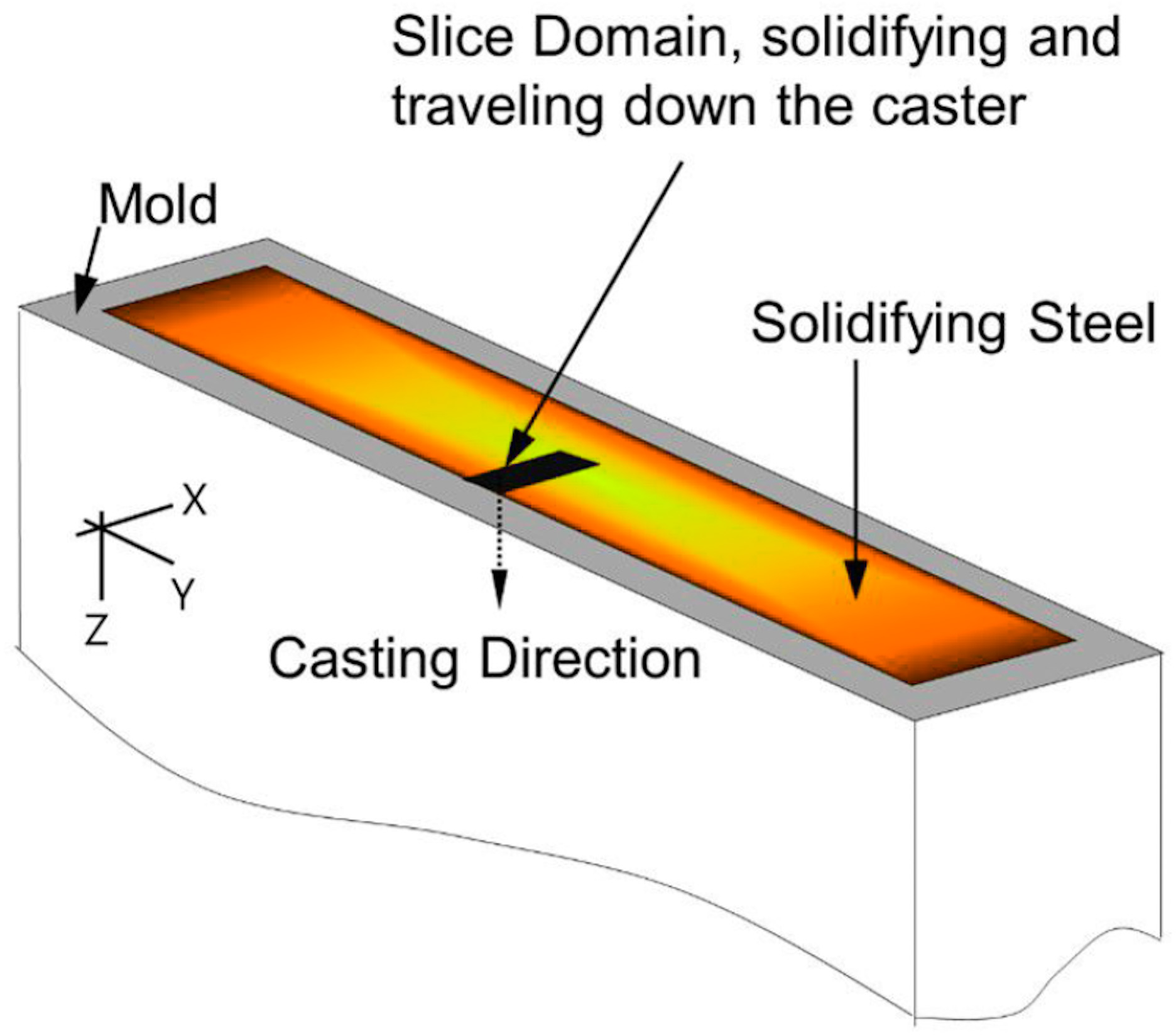
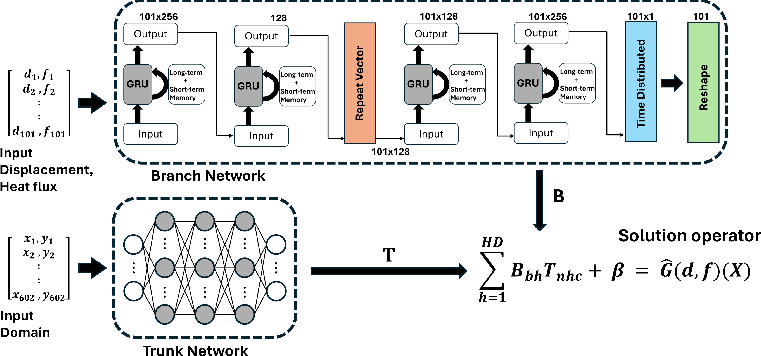
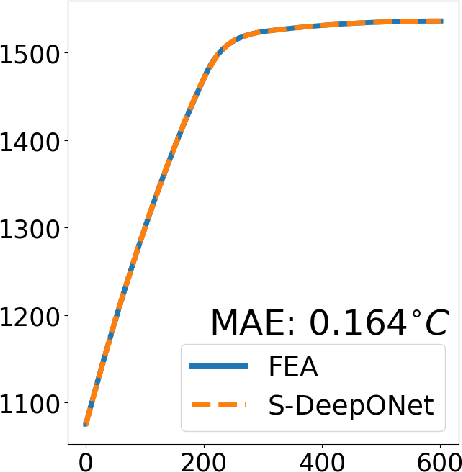
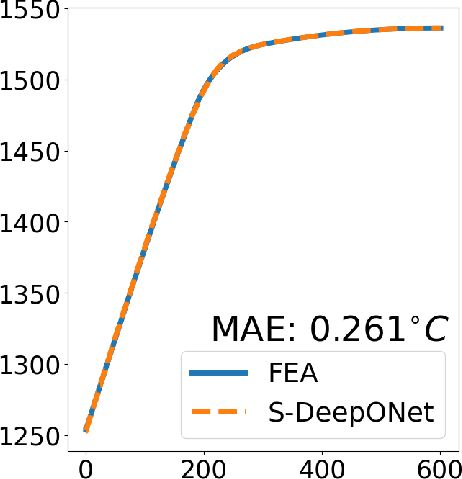
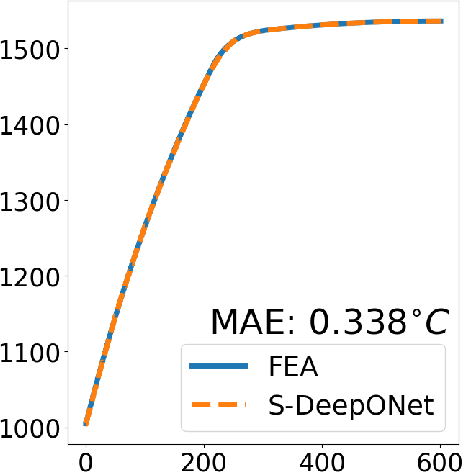
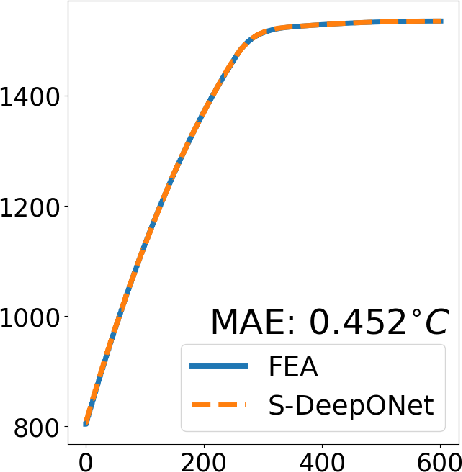
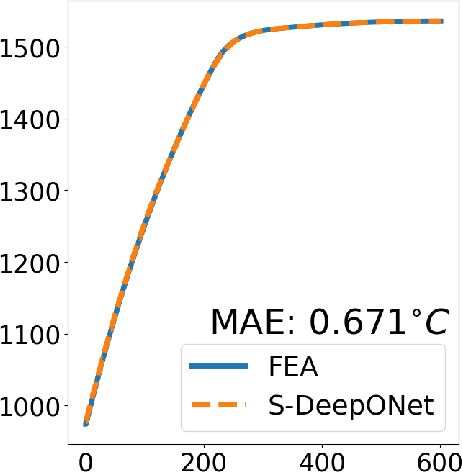
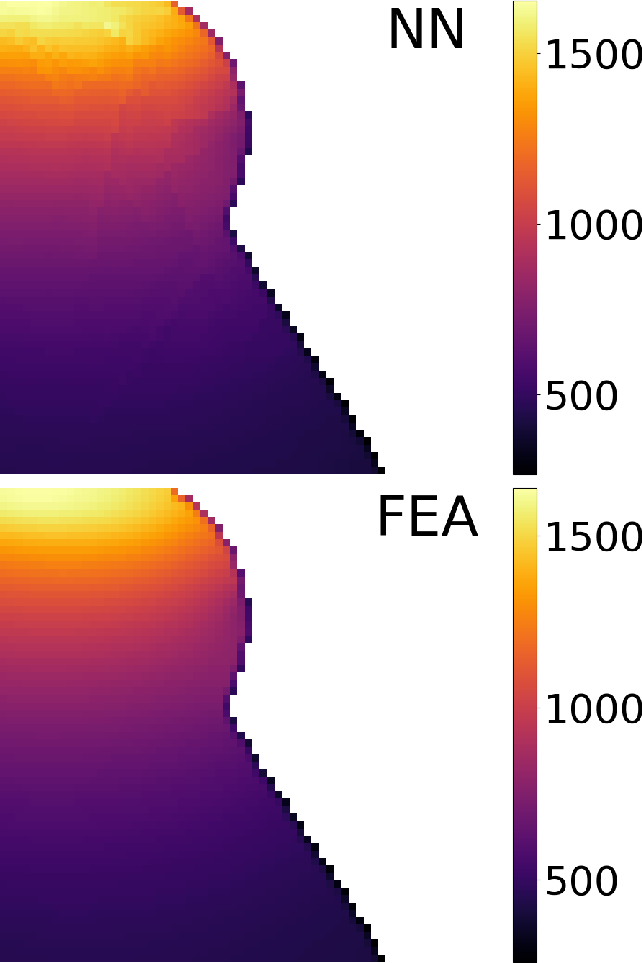
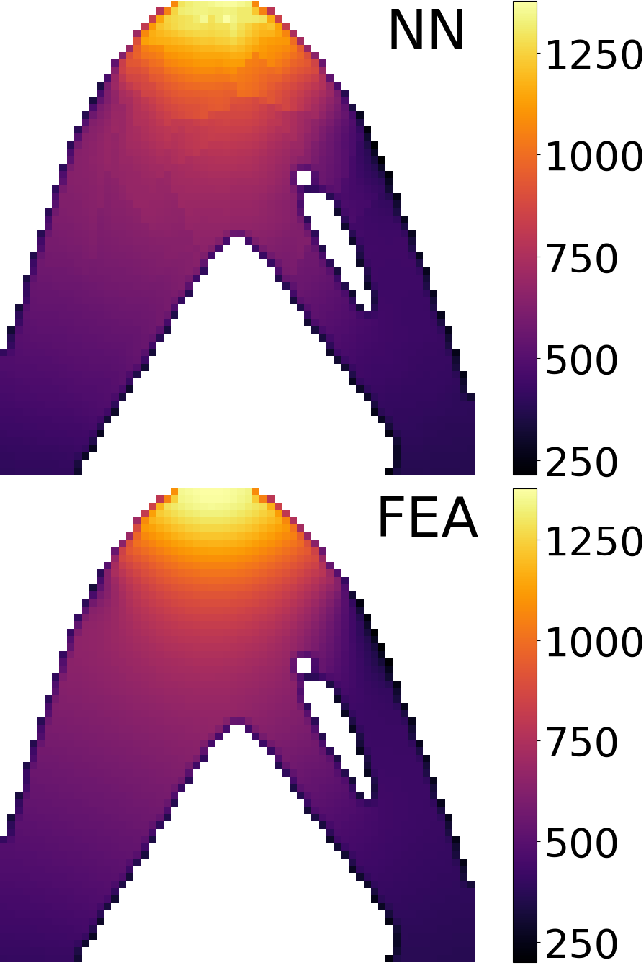
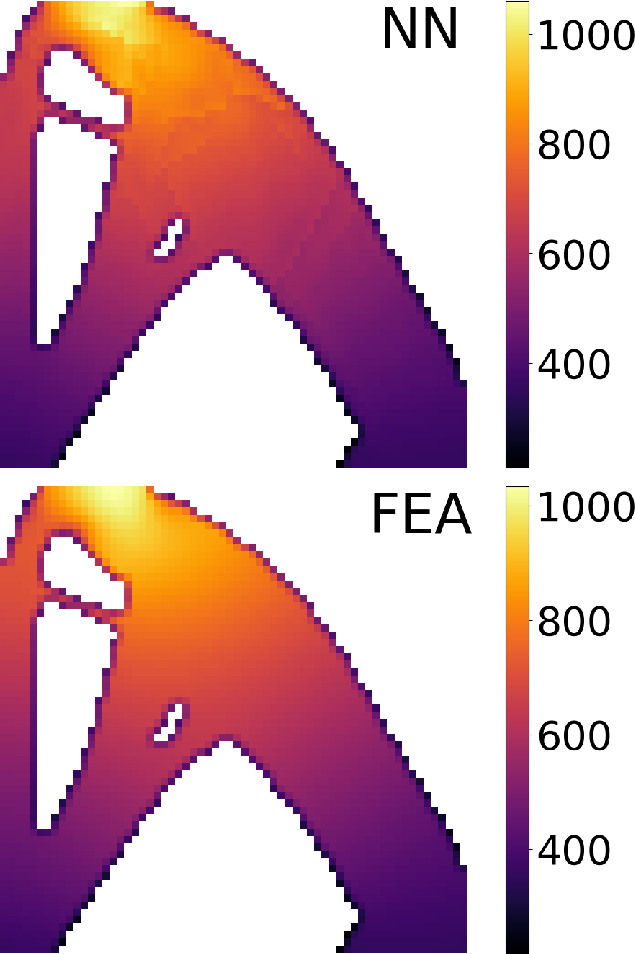
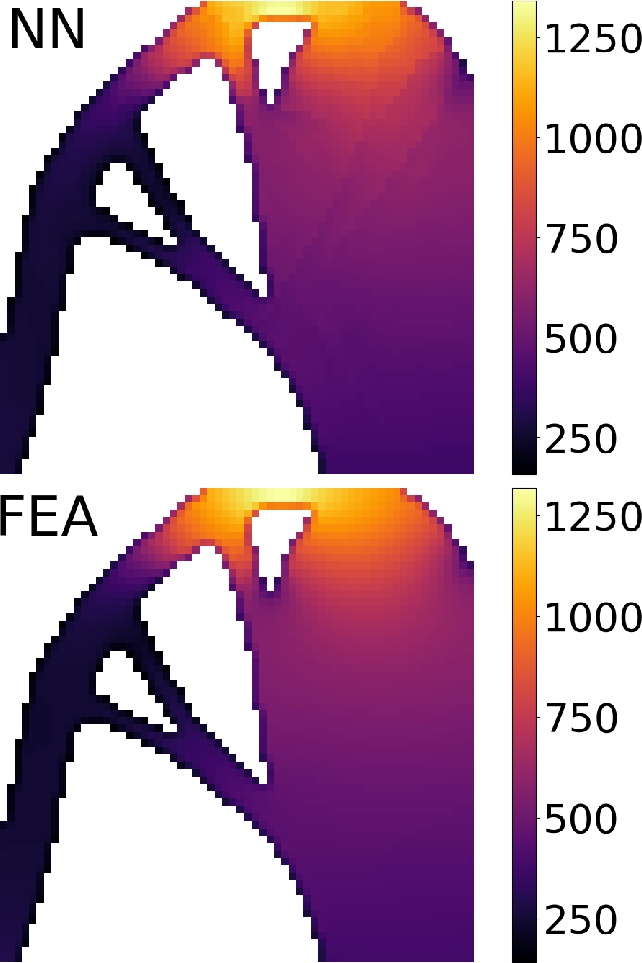
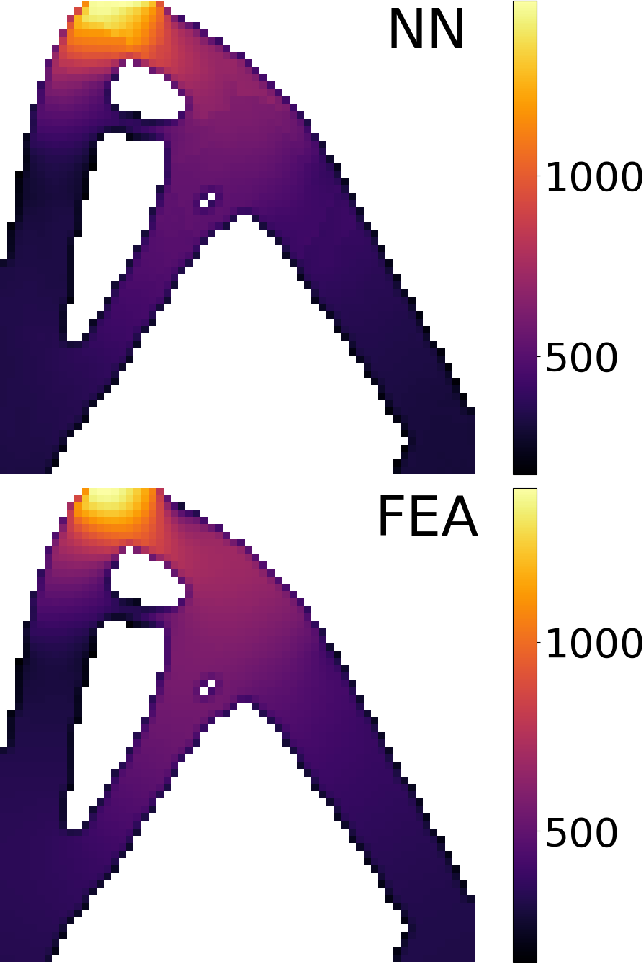
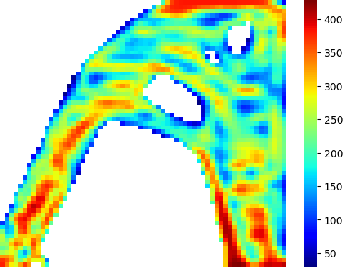
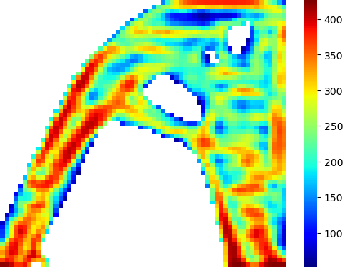
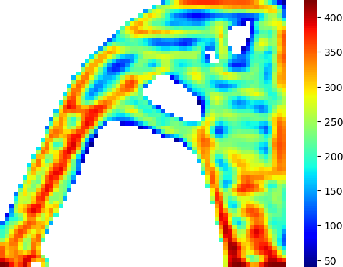
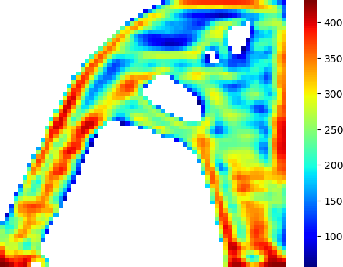
Advanced Deep Operator Networks to Predict Multiphysics Solution Fields in Materials Processing and Additive Manufacturing (2403.14795v1)

Abstract: Unlike classical artificial neural networks, which require retraining for each new set of parametric inputs, the Deep Operator Network (DeepONet), a lately introduced deep learning framework, approximates linear and nonlinear solution operators by taking parametric functions (infinite-dimensional objects) as inputs and mapping them to complete solution fields. In this paper, two newly devised DeepONet formulations with sequential learning and Residual U-Net (ResUNet) architectures are trained for the first time to simultaneously predict complete thermal and mechanical solution fields under variable loading, loading histories, process parameters, and even variable geometries. Two real-world applications are demonstrated: 1- coupled thermo-mechanical analysis of steel continuous casting with multiple visco-plastic constitutive laws and 2- sequentially coupled direct energy deposition for additive manufacturing. Despite highly challenging spatially variable target stress distributions, DeepONets can infer reasonably accurate full-field temperature and stress solutions several orders of magnitude faster than traditional and highly optimized finite-element analysis (FEA), even when FEA simulations are run on the latest high-performance computing platforms. The proposed DeepONet model's ability to provide field predictions almost instantly for unseen input parameters opens the door for future preliminary evaluation and design optimization of these vital industrial processes.

• The paper introduces advanced DeepONet architectures that combine GRU-based branch networks and ResUNet trunks to efficiently predict full-field multiphysics outcomes.
• It demonstrates significant computational speed-ups over traditional FEA, achieving up to 43,000x acceleration in stress predictions for additive manufacturing.
• The approach enables real-time multiphysics modeling, offering a promising tool for digital twins and iterative design optimization in industrial processes.

Advanced Deep Operator Networks for Multiphysics Problems

This essay provides a comprehensive summary of the paper titled "Advanced Deep Operator Networks to Predict Multiphysics Solution Fields in Materials Processing and Additive Manufacturing" (2403.14795). The paper introduces novel implementations of Deep Operator Networks (DeepONets) using S-DeepONet and ResUNet-based architectures, aimed at predicting full-field solutions in challenging real-world multiphysics problems, such as steel continuous casting and laser directed energy deposition (LDED) processes in additive manufacturing.

Introduction

The predictive modeling of multiphysics processes in manufacturing, such as continuous steel casting and additive manufacturing (AM), presents a complex challenge due to the intricate interactions between thermal, mechanical, and material properties. Traditional numerical methods, such as finite element analysis (FEA), are computationally intensive and struggle to perform real-time analysis over a wide range of parameters. The introduction of DeepONets offers a promising solution by learning mappings between input conditions and full-field outcomes, significantly accelerating the prediction process.

DeepONet Architectures: S-DeepONet and ResUNet-Based DeepONet

S-DeepONet for Steel Casting

S-DeepONet, an extension of the base DeepONet framework, incorporates a Gated Recurrent Unit (GRU) in its branch network to handle time-dependent inputs, coupled with a feed-forward neural network (FNN) as the trunk network for spatial inputs. This architecture is particularly suited for predicting the thermal and mechanical fields in the continuous casting of steel, where time-dependent thermal flux and displacement data influence the nonlinear solidification process.

$$\text{G}_{bnc} = \sum_{h=1}^{HD} \text{B}_{bh} \text{T}_{nhc} + \boldsymbol{\beta}$$

In this formulation, $\text{G}_{bnc}$ is the output operator, composed of branch ($\text{B}_{bh}$) and trunk ($\text{T}_{nhc}$) network outputs. Training this configuration allows the model to predict temperature and stress profiles across the steel casting process efficiently.

Figure 1: Continuous caster with solidifying slice finite element domain.

ResUNet-Based DeepONet for Additive Manufacturing

For AM processes, the ResUNet-based DeepONet introduces a ResUNet structure in the trunk network, enabling the handling of variable geometries along with printing process parameters like speed and material properties. This model is tasked with predicting the residual stress and temperature profiles in LDED, a particularly complex multiphysics problem because of the rapid material deposition and solidification under varying thermal conditions.

Figure 2: Architecture of the multi-component S-DeepONet for multiphysics problems. $d$ and $f$ represent the time-dependent input displacement and heat flux used in simulation, and $x$, $y$ are nodal coordinates. $\hat{G}$.

Implementation and Results

Steel Solidification with S-DeepONet

In continuous casting, S-DeepONet showcases superior predictive accuracy in determining lateral stress and temperature fields, critical in minimizing defects such as cracks during steel solidification. The model was trained on 10,000 data points, simulating various thermal flux and displacement boundary conditions, achieving a significant computational speed-up over FEA.

Figure 3: Temperature predictions by S-DeepONet compared to multiphysics FEA simulations in test dataset.

Additive Manufacturing with ResUNet-Based DeepONet

The application of ResUNet-based DeepONet in AM focused on predicting thermal and residual stress distributions across varying geometries and speeds. The model, trained on data from 4,574 simulations, demonstrated an average computational speed-up of 43,000 times compared to FEA while maintaining high accuracy in stress predictions, vital for optimizing AM processes to prevent residual stresses that can lead to failure.

Figure 4: Temperature predictions by ResUNet-based DeepONet compared to FEA for samples in the test dataset.

Implications and Future Directions

These advanced DeepONet architectures offer a transformative approach in understanding and optimizing industrial manufacturing processes, enabling real-time decision-making and design optimizations that were previously infeasible due to computational constraints. Their ability to generalize across unseen inputs without retraining positions them as ideal tools for digital twins and iterative design processes, particularly in AM and steel production.

Future work will look to expand these methods into fully three-dimensional simulations and incorporate multiscale physics interactions, marrying microstructural and macroscopic data to create even more robust predictive models. This evolution could provide critical insights for industries aiming to reduce defects and optimize production efficiency.

Figure 5: Stress prediction of a median sample, 5 different velocities.

In conclusion, the enhanced DeepONet architectures significantly push the frontiers in predictive modeling of highly complex multiphysics systems, hinting at broad applicability across various manufacturing technologies.