Instructing Large Language Models to Identify and Ignore Irrelevant Conditions (2403.12744v1)

Abstract: Math word problem (MWP) solving requires generating a reasoning path based on a given problem description that often contains irrelevant conditions. Existing chain-of-thought (CoT) prompting methods elicited multi-step reasoning abilities of LLMs to solve MWPs. However, they were seriously confused by the irrelevant conditions, resulting in low accuracy. In this paper, we propose a novel approach named I$^3$C that instructs LLMs to identify and ignore irrelevant conditions. It identifies a set of irrelevant condition candidates that have a weak semantic relevance with the question. Then it prompts LLMs to verify the irrelevant conditions. Lastly it instructs the LLMs with the verification on relevant and irrelevant conditions to avoid confusion and improve reasoning paths. Moreover, we propose to select (problem, reasoning paths) pairs as demonstrations to enhance I$^3$C with few-shot reasoning. We develop I$^3$C-Select that selects the most confusing problems based on the semantic relevance measurement. We conduct extensive experiments on eight MWP datasets. I$^3$C can be combined with any CoT prompting methods to improve the performance of solving MWPs. Notably, with GPT-3.5-Turbo and I$^3$C-Select, we achieve an accuracy of 96.0 and 94.1 on GSM-IC2-1K and GSM-ICM-1K, respectively, significantly outperforming the state-of-the-art few-shot prompting method Complex-CoT by +11.7 and +11.1. Our implementation is made publicly available at https://wzy6642.github.io/I3C.github.io/.

• The paper introduces I3C, a method instructing LLMs to detect and ignore irrelevant conditions, leading to more accurate reasoning in math word problems.
• It describes a three-step process of candidate identification, verification, and instruction integration, validated across eight MWP datasets.
• I3C-Select optimizes demonstration selection by choosing high-confusion problems, reducing computational costs while maintaining high accuracy.

Instructing LLMs to Ignore Irrelevant Conditions

The paper "Instructing LLMs to Identify and Ignore Irrelevant Conditions" (2403.12744) introduces I$^3$C, a novel approach designed to enhance LLM performance in solving MWPs. The key innovation involves instructing LLMs to explicitly identify and ignore irrelevant conditions, which often confuse existing CoT prompting methods. The paper demonstrates that by incorporating I$^3$C, LLMs can generate more accurate reasoning paths and achieve state-of-the-art results across a range of MWP datasets.

I$^3$C Methodology

The I$^3$C approach comprises three main steps: identifying irrelevant condition candidates, verifying their irrelevance, and leveraging these verifications to guide the LLM's reasoning process (Figure 1).

Figure 1: Existing CoT prompting methods were confused by irrelevant conditions in math word problems and gave wrong answers.

Initially, the method splits a MWP into individual conditions $\{c_i\}$ and a question sentence $q$. A pre-trained LLM, such as SimCSE, encodes these conditions and the question into vector representations, $\{\mathbf{c}_{i}\}$ and $\mathbf{q}$, respectively. The semantic relevance between each condition $c_i$ and the question $q$ is then quantified using cosine similarity, $s_{i}^{\text{(c)}}$ and $s_{i}^{\text{(q)}}$.

Conditions with low semantic relevance (i.e., $s_{i}^{\text{(c)}} < \theta$ or $s_{i}^{\text{(q)}} < \theta$) are flagged as irrelevant condition candidates, forming the set $\mathcal{I}=\{c_{k}^{(\mathrm{irr})}\}$. The threshold $\theta$ is a hyperparameter that controls the sensitivity of the irrelevance detection.

Next, an LLM is prompted to verify whether each candidate condition $c_{k}^{(\mathrm{irr})}$ is indeed irrelevant. The verification prompt takes the form: “$Q$. Is condition $c_{k^{(\mathrm{irr})}$ relevant to the process of solving problem $q$?" The LLM's response, $v_{k}^{(\mathrm{irr})}$, provides a justification for the relevance or irrelevance of the condition.

Finally, the verification outputs $\{v_{k}^{(\mathrm{irr})}\}$ are combined to create the I$^3$C instruction, denoted by $I$. This instruction is then prepended to any CoT prompting method, guiding the LLM to focus on relevant information and ignore irrelevant details.

Enhancements with I$^3$C-Select

To further enhance the performance of I$^3$C, the authors introduce I$^3$C-Select, a few-shot prompting method that automatically selects the most confusing problems as demonstrations. The confusion score of a problem $Q$ is defined as the inverse of the average similarity between its conditions and the question:

$$\text{conf}(Q) = \left[\frac{1}{n}\sum_{i=1}^n\cos{(\mathbf{c}_i, \mathbf{q})}\right]^{-1}$$

The $K$ problems with the highest confusion scores are selected, and their reasoning paths are generated using the Zero-Shot-CoT prompting method. These confusing problems and their reasoning paths serve as demonstrations for the LLM, enabling it to better handle complex scenarios with irrelevant conditions.

Experimental Evaluation and Results

The effectiveness of I$^3$C and I$^3$C-Select was evaluated on eight MWP datasets, including AddSub, SVAMP, GSM8K, SingleEq, GSM-IC2-1K, GSM-ICM-1K, AQuA, and MATH. The experiments demonstrate that adding the I$^3$C instruction to CoT prompting methods significantly improves their performance. For example, adding I$^3$C instruction to Manual-CoT improves the accuracy by $+8.1$ on AddSub, $+8.1$ on SVAMP, $+6.0$ on GSM8K, $+5.1$ on SingleEq, $+5.1$ on GSM-IC2-1K, $+2.8$ on AQuA, $+9.2$ on MATH, and $+7.8$ on GSM-ICM-1K. The most striking results were observed on datasets with a high proportion of irrelevant conditions, such as GSM-IC2-1K and GSM-ICM-1K. On these datasets, I$^3$C-Select achieved accuracy gains of $+11.7$ and $+11.1$, respectively, compared to the Complex-CoT method.

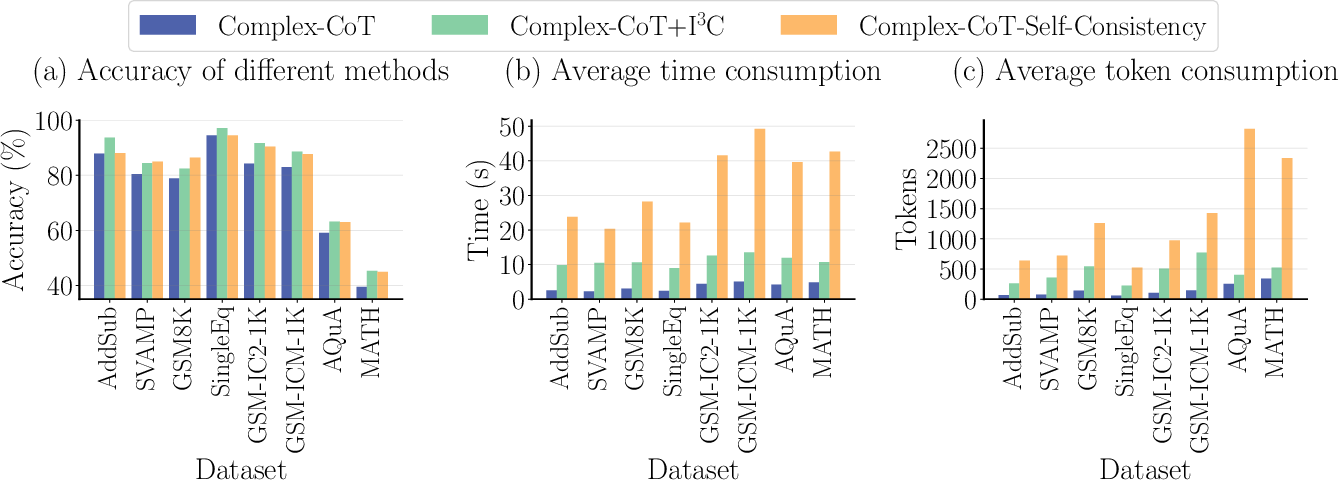
Figure 2: Performance comparison of Complex-CoT, Complex-CoT with I$^3$C instruction (i.e., Complex-CoT+I^3C), and Complex-CoT with self-consistency (i.e., Complex-CoT-Self-Consistency). We can observe that the accuracy of Complex-CoT+I^3C and Complex-CoT-Self-Consistency is nearly identical, while Complex-CoT+I^3C consumes much less tokens and time than Complex-CoT-Self-Consistency.

The authors also compared the performance of Complex-CoT with I$^3$C (Complex-CoT+I$^3$C) against Complex-CoT with self-consistency (Complex-CoT-Self-Consistency). The results showed that Complex-CoT+I$^3$C achieved nearly identical accuracy to Complex-CoT-Self-Consistency, while consuming significantly fewer tokens and time (Figure 2). This highlights the efficiency and effectiveness of the I$^3$C approach.

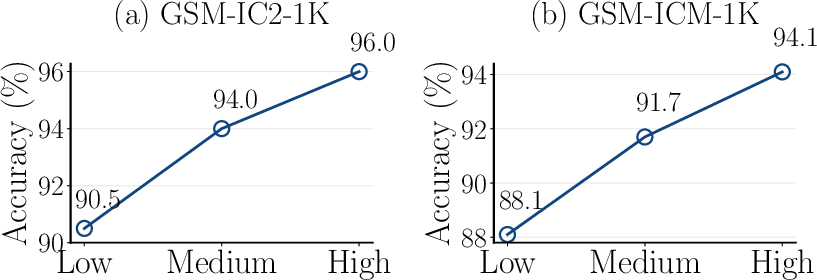
Figure 3: Demonstration construction methods comparison. Low'' indicates selecting eight problems with the lowest confusion scores.Medium'' indicates randomly selecting eight problems. ``High'' indicates selecting eight problems with the highest confusion scores.

Ablation studies were conducted to evaluate the impact of different demonstration construction methods on the performance of I$^3$C-Select. The results demonstrated that selecting the most confusing problems as demonstrations ("High") consistently outperformed selecting problems with the lowest confusion scores ("Low") or randomly selecting problems ("Medium") (Figure 3). This finding supports the hypothesis that focusing on the most challenging examples can effectively improve the LLM's ability to handle irrelevant conditions.

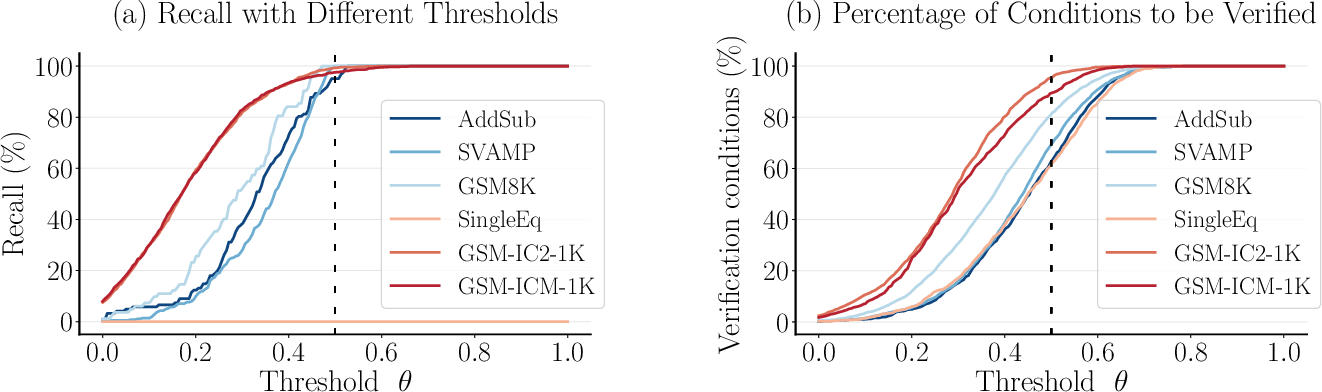
Figure 4: Hyperparameter analysis. (a) As the threshold increases, the recall scores of identified irrelevant condition candidates first increase and then remain unchanged for all datasets except SingleEq. (b) As the threshold increases, the percentage of conditions to be verified first increases and then remains unchanged for all datasets.

Hyperparameter analysis was performed to determine the optimal threshold $\theta$ for identifying irrelevant condition candidates. The results indicated that a threshold of $0.5$ provided a good balance between the recall of irrelevant conditions and the percentage of conditions requiring verification (Figure 4).

Implications and Future Directions

The I$^3$C approach has significant implications for the development of more robust and reliable LLMs. By explicitly addressing the issue of irrelevant conditions, I$^3$C enables LLMs to generate more accurate reasoning paths and improve their performance on complex problem-solving tasks. The plug-and-play nature of the I$^3$C module makes it easy to integrate into existing CoT prompting methods, providing a versatile tool for enhancing LLM capabilities.

Future research directions could explore the application of I$^3$C to other NLP tasks that are susceptible to irrelevant information, such as question answering and text summarization. Additionally, investigating the use of more sophisticated methods for identifying irrelevant conditions, such as employing more advanced semantic similarity measures or training dedicated irrelevance detection models, could further improve the performance of I$^3$C.

Conclusion

The paper "Instructing LLMs to Identify and Ignore Irrelevant Conditions" (2403.12744) presents a valuable contribution to the field of LLMs. The I$^3$C approach offers a practical and effective solution for mitigating the negative impact of irrelevant conditions on MWP solving performance. The experimental results demonstrate the superiority of I$^3$C and I$^3$C-Select over existing prompting methods, highlighting the potential of explicit instruction for enhancing LLM reasoning abilities.