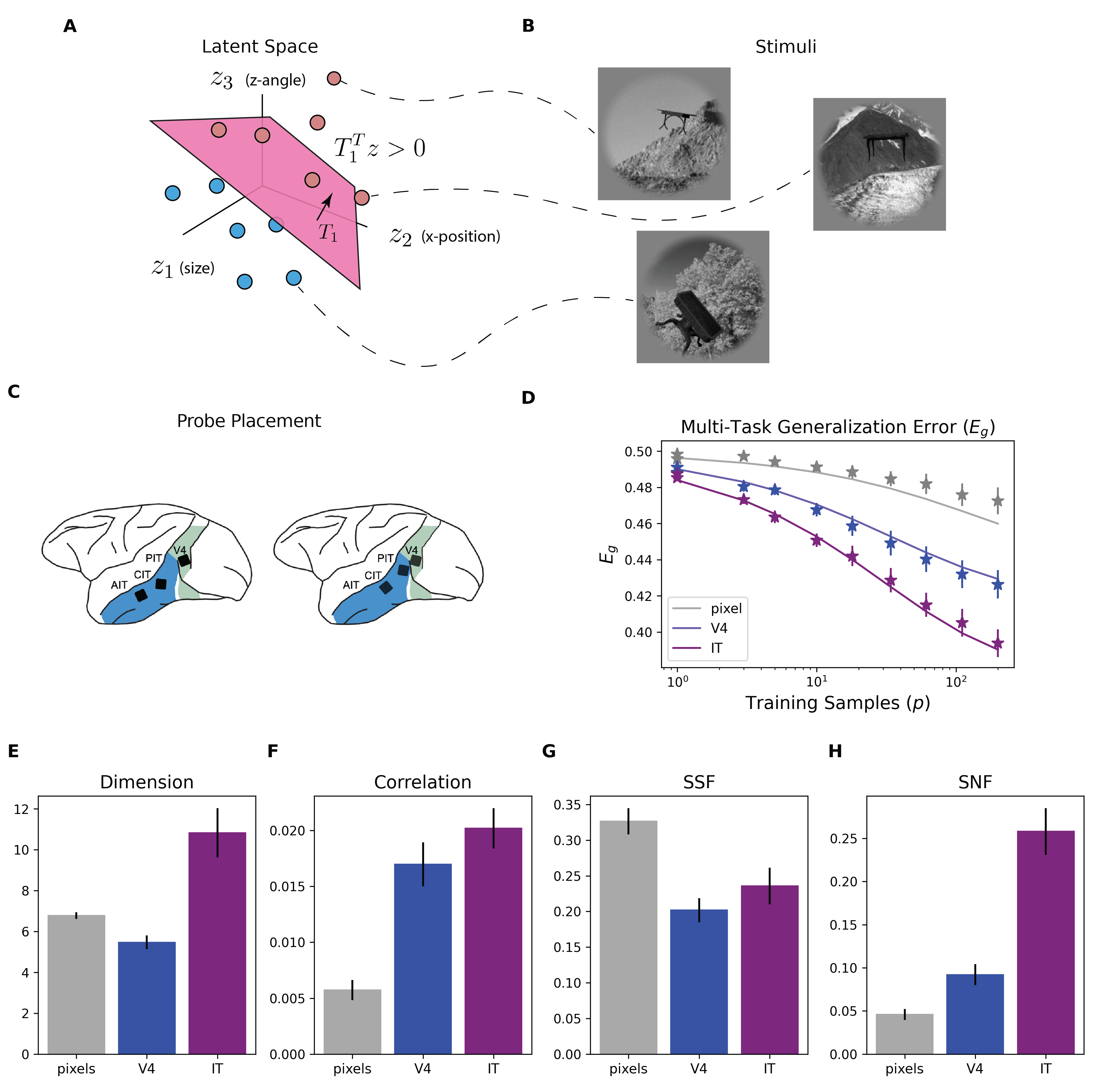
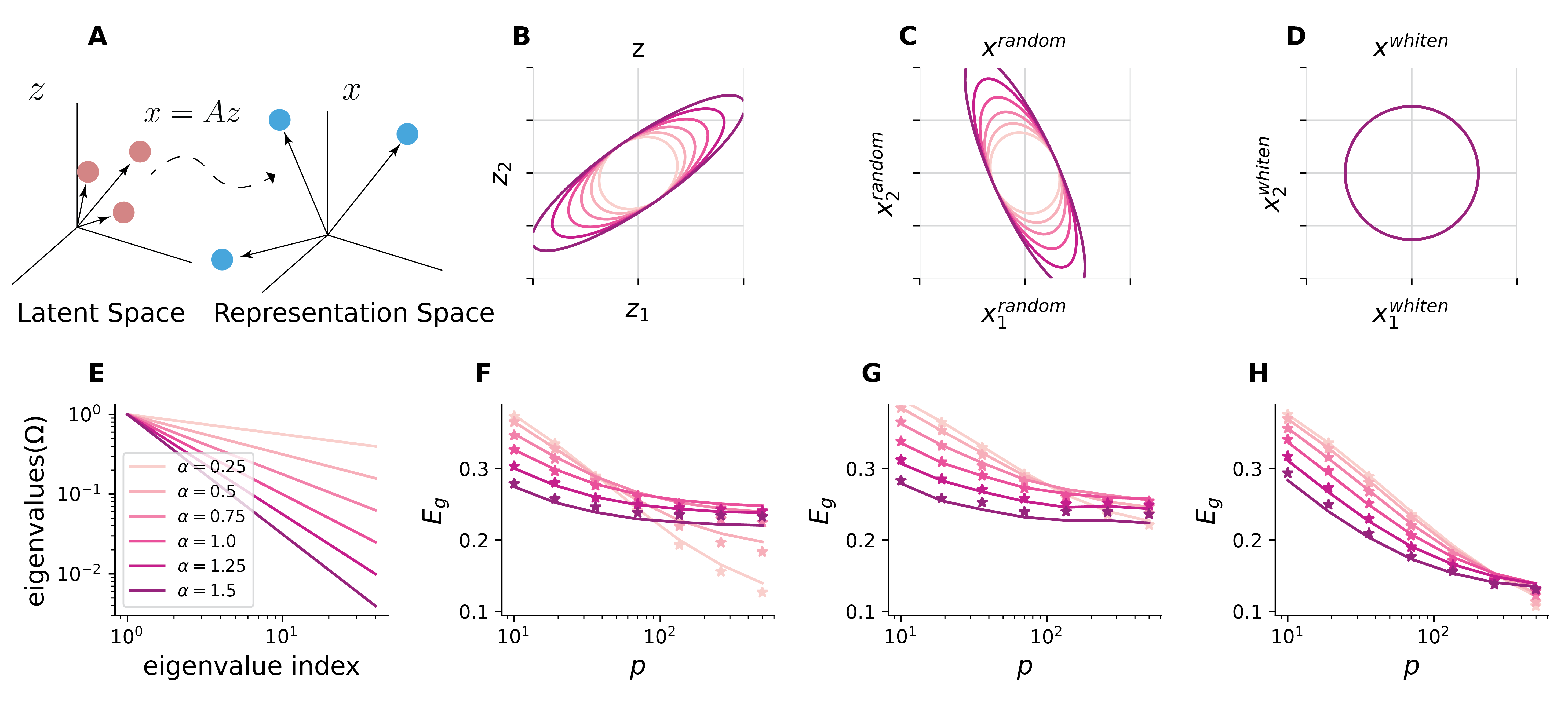Papers
Topics
Authors
Recent
Gemini 2.5 Flash
Gemini 2.5 Flash
97 tokens/sec
GPT-4o
53 tokens/sec
Gemini 2.5 Pro Pro
44 tokens/sec
o3 Pro
5 tokens/sec
GPT-4.1 Pro
47 tokens/sec
DeepSeek R1 via Azure Pro
28 tokens/sec
2000 character limit reached

Neural population geometry and optimal coding of tasks with shared latent structure (2402.16770v2)

Published 26 Feb 2024 in q-bio.NC, cond-mat.dis-nn, cond-mat.stat-mech, cs.LG, and cs.NE

Abstract: Humans and animals can recognize latent structures in their environment and apply this information to efficiently navigate the world. However, it remains unclear what aspects of neural activity contribute to these computational capabilities. Here, we develop an analytical theory linking the geometry of a neural population's activity to the generalization performance of a linear readout on a set of tasks that depend on a common latent structure. We show that four geometric measures of the activity determine performance across tasks. Using this theory, we find that experimentally observed disentangled representations naturally emerge as an optimal solution to the multi-task learning problem. When data is scarce, these optimal neural codes compress less informative latent variables, and when data is abundant, they expand these variables in the state space. We validate our theory using macaque ventral stream recordings. Our results therefore tie population geometry to multi-task learning.

Definition Search Book Streamline Icon: https://streamlinehq.com
References (60)
  1. Abstract representations emerge in human hippocampal neurons during inference behavior. bioRxiv, 2023.
  2. The geometry of cortical representations of touch in rodents. Nature Neuroscience, 26(2):239–250, 2023.
  3. Semi-orthogonal subspaces for value mediate a tradeoff between binding and generalization. ArXiv, 2023.
  4. The geometry of abstraction in the hippocampus and prefrontal cortex. Cell, 183(4):954–967, 2020.
  5. Unsupervised deep learning identifies semantic disentanglement in single inferotemporal face patch neurons. Nature communications, 12(1):6456, 2021.
  6. Le Chang and Doris Y Tsao. The code for facial identity in the primate brain. Cell, 169(6):1013–1028, 2017.
  7. Abstract representations emerge naturally in neural networks trained to perform multiple tasks. Nature Communications, 14(1):1040, 2023.
  8. Rotational dynamics reduce interference between sensory and memory representations. Nature neuroscience, 24(5):715–726, 2021.
  9. Towards a definition of disentangled representations. arXiv preprint arXiv:1812.02230, 2018.
  10. What is a cognitive map? organizing knowledge for flexible behavior. Neuron, 100(2):490–509, 2018.
  11. Mapping of a non-spatial dimension by the hippocampal–entorhinal circuit. Nature, 543(7647):719–722, March 2017.
  12. Hippocampal neurons construct a map of an abstract value space. Cell, 184(18):4640–4650.e10, September 2021.
  13. Geometry of abstract learned knowledge in the hippocampus. Nature, 595(7865):80–84, July 2021.
  14. Grid-like Neural Representations Support Olfactory Navigation of a Two-Dimensional Odor Space. Neuron, 102(5):1066–1075.e5, June 2019.
  15. Organizing conceptual knowledge in humans with a gridlike code. Science, 352(6292):1464–1468, June 2016.
  16. Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci., 31:69–89, 2008.
  17. Large-scale neural recordings call for new insights to link brain and behavior. Nature neuroscience, 25(1):11–19, 2022.
  18. SueYeon Chung and LF Abbott. Neural population geometry: An approach for understanding biological and artificial neural networks. Current opinion in neurobiology, 70:137–144, 2021.
  19. Classification and geometry of general perceptual manifolds. Physical Review X, 8(3):031003, 2018.
  20. Separability and geometry of object manifolds in deep neural networks. Nature communications, 11(1):746, 2020.
  21. Linear classification of neural manifolds with correlated variability. Physical Review Letters, 131(2):027301, 2023.
  22. Neural representational geometry underlies few-shot concept learning. Proceedings of the National Academy of Sciences, 119(43):e2200800119, 2022.
  23. Reorganization between preparatory and movement population responses in motor cortex. Nature communications, 7(1):13239, 2016.
  24. Motor cortex embeds muscle-like commands in an untangled population response. Neuron, 97(4):953–966, 2018.
  25. A neural population mechanism for rapid learning. Neuron, 100(4):964–976, 2018.
  26. Cerebellar granule cell axons support high-dimensional representations. Nature neuroscience, 24(8):1142–1150, 2021.
  27. High-dimensional geometry of population responses in visual cortex. Nature, 571(7765):361–365, 2019.
  28. The neural code for face memory. BioRxiv, pages 2021–03, 2021.
  29. Three unfinished works on the optimal storage capacity of networks. Journal of Physics A: Mathematical and General, 22(12):1983, 1989.
  30. Modeling the influence of data structure on learning in neural networks: The hidden manifold model. Physical Review X, 10(4):041044, 2020.
  31. Learning curves of generic features maps for realistic datasets with a teacher-student model. Advances in Neural Information Processing Systems, 34:18137–18151, 2021.
  32. A Engel and C Van den Broeck. Statistical Mechanics of Learning. Cambridge University Press, 2005.
  33. Simple learned weighted sums of inferior temporal neuronal firing rates accurately predict human core object recognition performance. Journal of Neuroscience, 35(39):13402–13418, 2015.
  34. dsprites: Disentanglement testing sprites dataset. https://github.com/deepmind/dsprites-dataset/, 2017.
  35. The gaussian equivalence of generative models for learning with shallow neural networks. In Mathematical and Scientific Machine Learning, pages 426–471. PMLR, 2022.
  36. Universality of max-margin classifiers. arXiv preprint arXiv:2310.00176, 2023.
  37. Origami in n dimensions: How feed-forward networks manufacture linear separability, 2022.
  38. Explicit information for category-orthogonal object properties increases along the ventral stream. Nature neuroscience, 19(4):613–622, 2016.
  39. Factorized visual representations in the primate visual system and deep neural networks. bioRxiv, pages 2023–04, 2023.
  40. Efficient sensory encoding and bayesian inference with heterogeneous neural populations. Neural computation, 26(10):2103–2134, 2014.
  41. Towards a theory of early visual processing. Neural computation, 2(3):308–320, 1990.
  42. Efficient coding of spatial information in the primate retina. Journal of Neuroscience, 32(46):16256–16264, 2012.
  43. The hippocampus as a predictive map. Nature neuroscience, 20(11):1643–1653, 2017.
  44. Neural learning rules for generating flexible predictions and computing the successor representation. Elife, 12:e80680, 2023.
  45. A unified theory for the computational and mechanistic origins of grid cells. Neuron, 111(1):121–137, 2023.
  46. The successor representation in human reinforcement learning. Nature human behaviour, 1(9):680–692, 2017.
  47. Ida Momennejad. Learning structures: predictive representations, replay, and generalization. Current Opinion in Behavioral Sciences, 32:155–166, 2020.
  48. Task-dependent optimal representations for cerebellar learning. Elife, 12:e82914, 2023.
  49. Sparseness and expansion in sensory representations. Neuron, 83(5):1213–1226, 2014.
  50. Optimal degrees of synaptic connectivity. Neuron, 93(5):1153–1164, 2017.
  51. Optimal routing to cerebellum-like structures. Nature neuroscience, 26(9):1630–1641, 2023.
  52. Interpreting neural computations by examining intrinsic and embedding dimensionality of neural activity. Current opinion in neurobiology, 70:113–120, 2021.
  53. Spectrum dependent learning curves in kernel regression and wide neural networks. In International Conference on Machine Learning, pages 1024–1034. PMLR, 2020.
  54. Spectral bias and task-model alignment explain generalization in kernel regression and infinitely wide neural networks. Nature communications, 12(1):2914, 2021.
  55. Population codes enable learning from few examples by shaping inductive bias. Elife, 11:e78606, 2022.
  56. A spectral theory of neural prediction and alignment. In Thirty-seventh Conference on Neural Information Processing Systems, 2023.
  57. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv preprint arXiv:1312.6120, 2013.
  58. A mathematical theory of semantic development in deep neural networks. Proceedings of the National Academy of Sciences, 116(23):11537–11546, 2019.
  59. Theoretical neuroscience: computational and mathematical modeling of neural systems. MIT press, 2005.
  60. Adam: A method for stochastic optimization, 2017.
User Edit Pencil Streamline Icon: https://streamlinehq.com
Authors (3)
  1. Albert J. Wakhloo (2 papers)
  2. Will Slatton (1 paper)
  3. SueYeon Chung (30 papers)
Citations (1)
View on Semantic Scholar

Summary

We haven't generated a summary for this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Summarize Now