Papers
Topics
Authors
Recent
Gemini 2.5 Flash
Gemini 2.5 Flash
41 tokens/sec
GPT-4o
59 tokens/sec
Gemini 2.5 Pro Pro
41 tokens/sec
o3 Pro
7 tokens/sec
GPT-4.1 Pro
50 tokens/sec
DeepSeek R1 via Azure Pro
28 tokens/sec
2000 character limit reached

The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains (2402.11004v1)

Published 16 Feb 2024 in cs.LG

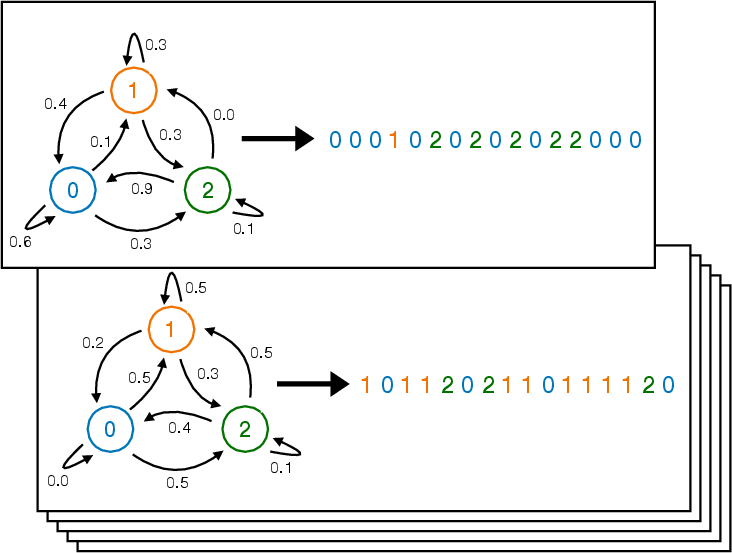
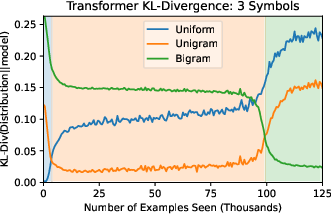
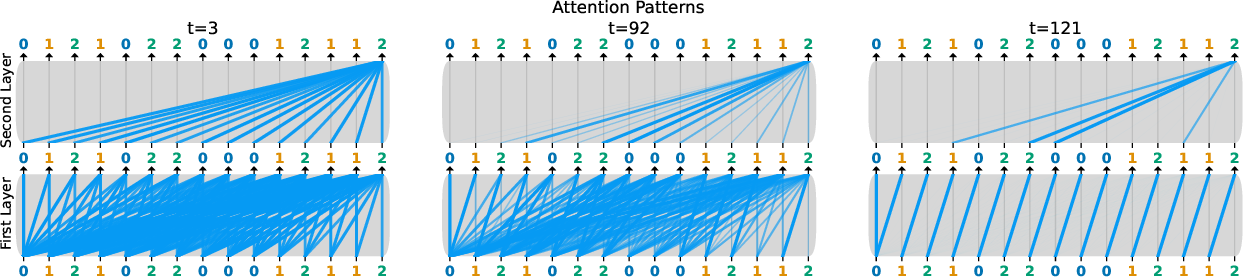
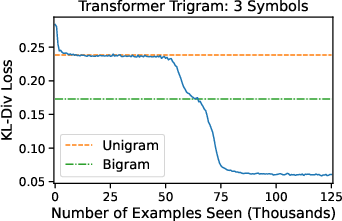
Abstract: LLMs have the ability to generate text that mimics patterns in their inputs. We introduce a simple Markov Chain sequence modeling task in order to study how this in-context learning (ICL) capability emerges. In our setting, each example is sampled from a Markov chain drawn from a prior distribution over Markov chains. Transformers trained on this task form \emph{statistical induction heads} which compute accurate next-token probabilities given the bigram statistics of the context. During the course of training, models pass through multiple phases: after an initial stage in which predictions are uniform, they learn to sub-optimally predict using in-context single-token statistics (unigrams); then, there is a rapid phase transition to the correct in-context bigram solution. We conduct an empirical and theoretical investigation of this multi-phase process, showing how successful learning results from the interaction between the transformer's layers, and uncovering evidence that the presence of the simpler unigram solution may delay formation of the final bigram solution. We examine how learning is affected by varying the prior distribution over Markov chains, and consider the generalization of our in-context learning of Markov chains (ICL-MC) task to $n$-grams for $n > 2$.

PDF HTML Abstract

Analyzing In-Context Learning in Transformers through Markov Chains

Overview

The paper investigates the capability of LLMs to perform in-context learning (ICL) by analyzing their training on a synthetic task designed around Markov chains. This approach aims to elucidate the mechanisms by which transformers process and learn from structured data sequences, focusing particularly on the emergence of statistical induction heads. The investigation reveals the underlying dynamics of learning by transformers when exposed to tasks that involve sequential data with intricate dependencies.

Methodology

The authors propose an in-context learning of Markov chains (ICL-MC) task, in which examples are derived from various Markov chains with randomly generated transition matrices. The age-old nn-gram models serve as the mathematical foundation, allowing researchers to model linguistic sequence prediction based on bigram statistics. Transformers, configured to solve the ICL-MC task, undergo a series of training phases that encapsulate:

  1. Uniform Prediction: Initially, transformers exhibit uniform prediction behavior.
  2. Unigram Phase: Learned unigram statistics form the basis of a less complex prediction model.
  3. Bigram Phase Transition: A rapid transition occurs, where models subsequently form a more complex prediction model utilizing bigram statistics.

Empirical validation accompanies theoretical analysis to uncover mechanisms that delay optimal learning due to simpler unigram solutions, impeding faster convergence on the bigram model. The research sheds light on the importance of inter-layer communication within transformers, portraying that alignment among layers is pivotal for successful phase transitions.

Empirical Insights and Theoretical Exploration

The analysis showcases the development of statistical induction heads within transformers. These sub-components focus on recent tokens, heightening probabilities for tokens that follow within the context—attaining performance close to the Bayes-optimal transition modeling. Layer synchrony within transformers ensures that learning advances hierarchically, from simple to complex representations. Interestingly, the simplicity bias of transformers, causing a predisposed attachment to unigram solutions, is explored as a critical contributor to learning dynamics. When these solutions are less aligned with the task at hand, convergence accelerates, illuminating valuable insights into training policies for faster model adaptations.

n-Gram Generalization

The narrative extends beyond bigrams, exploring the complexity introduced by n-grams (n>2n > 2). Here, transformers faced with nn-gram sequences exhibit an analogous hierarchical learning progression, underscoring the robustness and adaptability of these models to increasingly complex conditional distributions. The paper delights in drawing parallels to natural language processing tasks, arguing for a deeper examination into the emergent properties of attention mechanisms as they form across diverse sequential learning problems.

Implications and Future Directions

The insights matured from modeling simple sequential tasks like ICL-MC can invigorate further exploration into the optimization of transformers for real-world text data. Such understanding promotes designing models adept at rapidly learning patterns from data without extensive supervision. By detailing the phase-transition phenomena along with simplicity bias, the paper provides a theoretical touchstone for refining in-context learning capabilities. Future research will likely explore alternative architectures and learning paradigms that can circumvent simplicity bias or harness hierarchical dynamic learning as a lever for improving transformer efficiency and interpretability in complex scenarios.

Understanding how LLMs like transformers develop their in-context learning faculties ensures that AI systems advance towards better efficiency and adaptability, reducing computational overheads while maximizing output fidelity on contextual, real-world data applications.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown Bookmark Chat Bubble Oval Streamline Icon: https://streamlinehq.com Chat (Pro)
Definition Search Book Streamline Icon: https://streamlinehq.com
References (43)
  1. Sgd learning on neural networks: leap complexity and saddle-to-saddle dynamics. In The Thirty Sixth Annual Conference on Learning Theory, pages 2552–2623. PMLR.
  2. A mechanism for sample-efficient in-context learning for sparse retrieval tasks. CoRR, abs/2305.17040.
  3. What learning algorithm is in-context learning? investigations with linear models. arXiv preprint arXiv:2211.15661.
  4. In-context language learning: Architectures and algorithms. CoRR, abs/2401.12973.
  5. A closer look at memorization in deep networks. In International conference on machine learning, pages 233–242. PMLR.
  6. High-dimensional asymptotics of feature learning: How one gradient step improves the representation. In Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., and Oh, A., editors, Advances in Neural Information Processing Systems 35: Annual Conference on Neural Information Processing Systems 2022, NeurIPS 2022, New Orleans, LA, USA, November 28 - December 9, 2022.
  7. Hidden progress in deep learning: Sgd learns parities near the computational limit. Advances in Neural Information Processing Systems, 35:21750–21764.
  8. Curriculum learning. In Danyluk, A. P., Bottou, L., and Littman, M. L., editors, Proceedings of the 26th Annual International Conference on Machine Learning, ICML 2009, Montreal, Quebec, Canada, June 14-18, 2009, volume 382 of ACM International Conference Proceeding Series, pages 41–48. ACM.
  9. Birth of a transformer: A memory viewpoint.
  10. Circular law theorem for random markov matrices. Probability Theory and Related Fields, 152.
  11. Class-based n-gram models of natural language. Comput. Linguist., 18(4):467–479.
  12. Language models are few-shot learners. In Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., and Lin, H., editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual.
  13. Data distributional properties drive emergent in-context learning in transformers. Advances in Neural Information Processing Systems, 35:18878–18891.
  14. Sudden drops in the loss: Syntax acquisition, phase transitions, and simplicity bias in mlms.
  15. Chomsky, N. (1956). Three models for the description of language. IRE Transactions on information theory, 2(3):113–124.
  16. Why can gpt learn in-context? language models secretly perform gradient descent as meta optimizers. arXiv preprint arXiv:2212.10559.
  17. A survey for in-context learning. arXiv preprint arXiv:2301.00234.
  18. A mathematical framework for transformer circuits. Transformer Circuits Thread, 1.
  19. What can transformers learn in-context? A case study of simple function classes. In Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., and Oh, A., editors, Advances in Neural Information Processing Systems 35: Annual Conference on Neural Information Processing Systems 2022, NeurIPS 2022, New Orleans, LA, USA, November 28 - December 9, 2022.
  20. How do transformers learn in-context beyond simple functions? a case study on learning with representations. arXiv preprint arXiv:2310.10616.
  21. In-context learning creates task vectors. In Findings of the Association for Computational Linguistics: EMNLP 2023, pages 9318–9333.
  22. The developmental landscape of in-context learning. CoRR, abs/2402.02364.
  23. Neural tangent kernel: Convergence and generalization in neural networks. In Bengio, S., Wallach, H. M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., and Garnett, R., editors, Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, December 3-8, 2018, Montréal, Canada, pages 8580–8589.
  24. Sgd on neural networks learns functions of increasing complexity. Advances in neural information processing systems, 32.
  25. Karpathy, A. (2023). Mingpt. https://github.com/karpathy/minGPT/tree/master.
  26. General-purpose in-context learning by meta-learning transformers. CoRR, abs/2212.04458.
  27. Grokking as the transition from lazy to rich training dynamics. CoRR, abs/2310.06110.
  28. Transformers as algorithms: Generalization and stability in in-context learning. In International Conference on Machine Learning, pages 19565–19594. PMLR.
  29. Dichotomy of early and late phase implicit biases can provably induce grokking. CoRR, abs/2311.18817.
  30. Attention with markov: A framework for principled analysis of transformers via markov chains. CoRR, abs/2402.04161.
  31. A tale of two circuits: Grokking as competition of sparse and dense subnetworks. CoRR, abs/2303.11873.
  32. In-context learning and induction heads. Transformer Circuits Thread. https://transformer-circuits.pub/2022/in-context-learning-and-induction-heads/index.html.
  33. Grokking: Generalization beyond overfitting on small algorithmic datasets. arXiv preprint arXiv:2201.02177.
  34. Reddy, G. (2023). The mechanistic basis of data dependence and abrupt learning in an in-context classification task.
  35. Are emergent abilities of large language models a mirage? CoRR, abs/2304.15004.
  36. The pitfalls of simplicity bias in neural networks. Advances in Neural Information Processing Systems, 33:9573–9585.
  37. Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3):379–423.
  38. Self-attention with relative position representations. In Walker, M. A., Ji, H., and Stent, A., editors, Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT, New Orleans, Louisiana, USA, June 1-6, 2018, Volume 2 (Short Papers), pages 464–468. Association for Computational Linguistics.
  39. Deep learning generalizes because the parameter-function map is biased towards simple functions. arXiv preprint arXiv:1805.08522.
  40. Attention is all you need. In Guyon, I., von Luxburg, U., Bengio, S., Wallach, H. M., Fergus, R., Vishwanathan, S. V. N., and Garnett, R., editors, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 5998–6008.
  41. Transformers learn in-context by gradient descent. In International Conference on Machine Learning, pages 35151–35174. PMLR.
  42. How many pretraining tasks are needed for in-context learning of linear regression? arXiv preprint arXiv:2310.08391.
  43. An explanation of in-context learning as implicit bayesian inference. In The Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, April 25-29, 2022.
User Edit Pencil Streamline Icon: https://streamlinehq.com
Authors (5)
  1. Benjamin L. Edelman (11 papers)
  2. Ezra Edelman (2 papers)
  3. Surbhi Goel (44 papers)
  4. Eran Malach (37 papers)
  5. Nikolaos Tsilivis (11 papers)
Citations (29)
View on Semantic Scholar
Youtube Logo Streamline Icon: https://streamlinehq.com

YouTube