Thompson Sampling in Partially Observable Contextual Bandits (2402.10289v1)

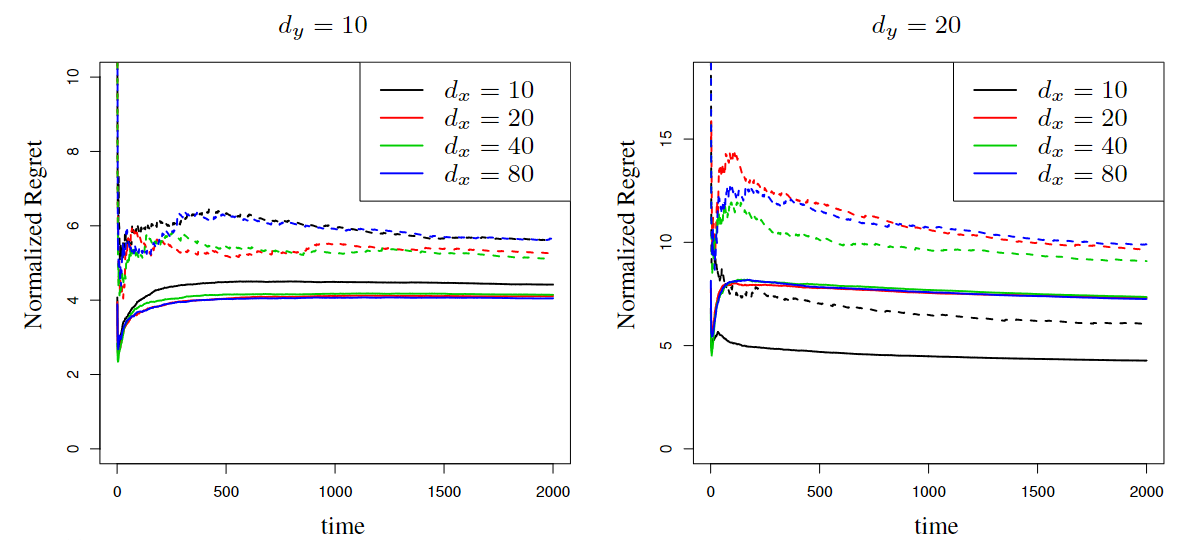
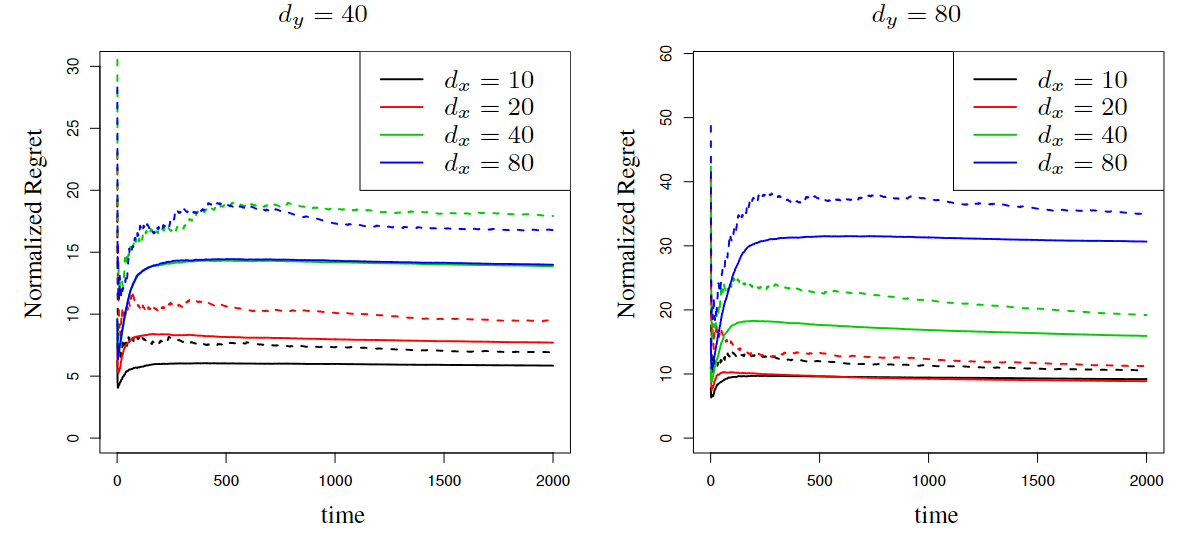
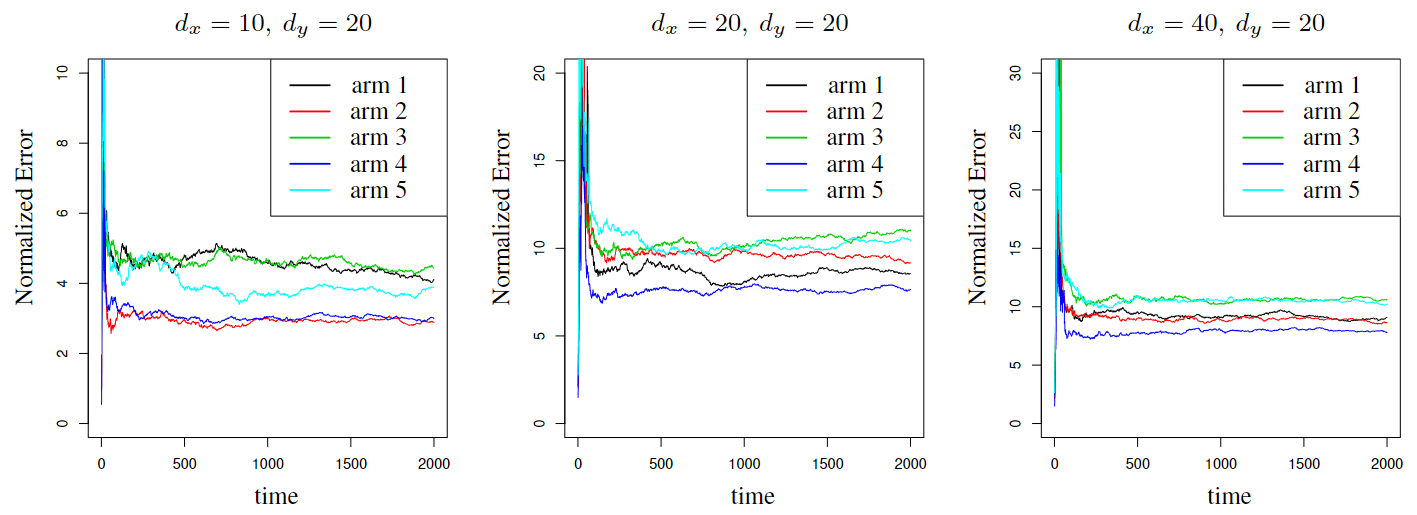
Abstract: Contextual bandits constitute a classical framework for decision-making under uncertainty. In this setting, the goal is to learn the arms of highest reward subject to contextual information, while the unknown reward parameters of each arm need to be learned by experimenting that specific arm. Accordingly, a fundamental problem is that of balancing exploration (i.e., pulling different arms to learn their parameters), versus exploitation (i.e., pulling the best arms to gain reward). To study this problem, the existing literature mostly considers perfectly observed contexts. However, the setting of partial context observations remains unexplored to date, despite being theoretically more general and practically more versatile. We study bandit policies for learning to select optimal arms based on the data of observations, which are noisy linear functions of the unobserved context vectors. Our theoretical analysis shows that the Thompson sampling policy successfully balances exploration and exploitation. Specifically, we establish the followings: (i) regret bounds that grow poly-logarithmically with time, (ii) square-root consistency of parameter estimation, and (iii) scaling of the regret with other quantities including dimensions and number of arms. Extensive numerical experiments with both real and synthetic data are presented as well, corroborating the efficacy of Thompson sampling. To establish the results, we introduce novel martingale techniques and concentration inequalities to address partially observed dependent random variables generated from unspecified distributions, and also leverage problem-dependent information to sharpen probabilistic bounds for time-varying suboptimality gaps. These techniques pave the road towards studying other decision-making problems with contextual information as well as partial observations.

• The paper introduces a novel Thompson sampling approach for contextual bandits with noisy, partially observable contexts, achieving bounded regret.
• It employs an observation model that samples from a hypothetical posterior distribution to update reward parameter estimates under incomplete context data.
• The method demonstrates sample efficiency and consistency, validated by theoretical regret bounds and empirical comparisons with regression and Greedy algorithms.

Thompson Sampling in Partially Observable Contextual Bandits

Introduction

The paper "Thompson Sampling in Partially Observable Contextal Bandits" (2402.10289) introduces a novel approach toward decision-making in the contextual bandit framework, where context observations are not perfect. This work distinguishes itself by focusing on situations where only partial, noisy, or transformed observations of contextual information are available, highlighting the practical applicability in areas like robotics, image processing, and healthcare, where perfect information is rarely accessible.

The paper advances existing methodologies by investigating the Thompson sampling strategy within this partially observable context, providing not only theoretical insights but also practical implementations. Key contributions include demonstrating that Thompson sampling maintains effectiveness even with partial observability, evidenced by bounded regret and consistent parameter estimation.

Problem Formulation

The fundamental challenge addressed in this work is balancing exploration and exploitation when making decisions under uncertainty, given incomplete context information. The rewards follow a model where the reward of an arm at any time is governed by the inner product of an unobserved context vector and an arm-specific parameter vector. Formally, the observed rewards incorporate noise to account for the unobserved aspects of the contexts, expressed as:

$r_i(t) = x_i(t)^\top \mu_i + \varepsilon_i(t)$

Where $x_i(t)$ is the latent context vector for arm $i$, $\mu_i$ is the unknown parameter vector for arm $i$, and $\varepsilon_i(t)$ is the stochastic noise.

Proposed Method

The authors propose the implementation of Thompson sampling by adapting it to work effectively with partially observable contexts. This involves:

1. Observation Model: The policy observes noisy linear transformations of context vectors: $y_i(t) = Ax_i(t) + \xi_i(t)$ where $A$ is an unknown sensing matrix and $\xi_i(t)$ is noise.
2. Hypothetical Posterior: To circumvent the lack of full context observability, the paper proposes using a hypothetical posterior distribution for the reward parameters based on the observed data, updating belief distributions through:

$r_i(t) \sim \mathcal{N}(y_i(t)^\top \eta_i, v^2)$

where $\eta_i = D^\top \mu_i$, and $D$ is a transformation matrix.

1. Algorithm Implementation: The Thompson sampling algorithm is executed by iteratively sampling from the posterior distribution and selecting the arm to maximize expected reward based on the sampled parameter.

Theoretical Analysis

Key theoretical results are derived, providing assurances about the method's performance:

1. Regret Bound: A significant result is the derivation of a regret bound, growing poly-logarithmically with time, indicating efficient performance preservation even with partial observability.

Figure 1: Plots of $\mathrm{Regret}(t)/(\log t)^2$ across various context dimensions $d_x$ and $d_y$.

1. Estimation Consistency: The estimate of $\eta_i$ achieves square-root consistency with respect to the number of times an arm is chosen, demonstrating robustness in learning the underlying parameters of the model.
2. Sample Efficiency: Explicit bounds are provided for the minimum number of samples needed before achieving reliable estimates, along with conditions tailored for high-probability performance guarantees.

Experimental Evaluation

The efficacy of the proposal is validated against real-world data, illustrating scenarios of eye movement and EEG datasets showcasing the decision rates of Thompson sampling relative to a regression oracle.

Figure 2: Plots of normalized estimation errors as a function of time for multiple arm scenarios.

Figure 3: Comparative regret trajectories between Thompson sampling and Greedy algorithms with varying arm counts.

Conclusion

This work enriches the bandit literature by demonstrating Thompson sampling's versatility in contexts with observation imperfections. The empirical and theoretical findings assert that Thompson sampling remains a competitive choice, offering robust performance under uncertainty. Future work could further scrutinize adaptive algorithms within more complex observation structures or leverage non-linear transformations to enrich the decision-making landscape in practical applications.

This synthesis of theoretical scaffolding and empirical substantiation establishes a robust foundation, poised to foster subsequent innovations in adaptive decision-making systems operating under informational constraints.