Convergence Analysis of a Variable Projection Method for Regularized Separable Nonlinear Inverse Problems (2402.08568v1)

Abstract: Variable projection methods prove highly efficient in solving separable nonlinear least squares problems by transforming them into a reduced nonlinear least squares problem, typically solvable via the Gauss-Newton method. When solving large-scale separable nonlinear inverse problems with general-form Tikhonov regularization, the computational demand for computing Jacobians in the Gauss-Newton method becomes very challenging. To mitigate this, iterative methods, specifically LSQR, can be used as inner solvers to compute approximate Jacobians. This article analyzes the impact of these approximate Jacobians within the variable projection method and introduces stopping criteria to ensure convergence. We also present numerical experiments where we apply the proposed method to solve a blind deconvolution problem to illustrate and confirm our theoretical results.

• The paper introduces the Inexact-GenVarPro method to reduce computational costs by approximating Jacobians in regularized problems.
• It provides rigorous convergence analysis, confirming robust efficiency even with iterative LSQR approximations under varied conditions.
• Numerical experiments on blind deconvolution validate the method’s practical performance against resource-intensive exact computations.

Convergence Analysis of a Variable Projection Method for Regularized Separable Nonlinear Inverse Problems

Introduction

The paper presents a convergence analysis of a variable projection method tailored for solving regularized separable nonlinear inverse problems. Separable nonlinear least squares problems are transformed into reduced nonlinear least squares problems using variable projection techniques. The primary challenge in such problems is the computational cost associated with evaluating the Jacobians when applying the Gauss-Newton method. To alleviate this, the paper proposes using iterative methods like LSQR for approximating the Jacobians to ensure convergence of solutions.

Variable Projection for Regularized Problems

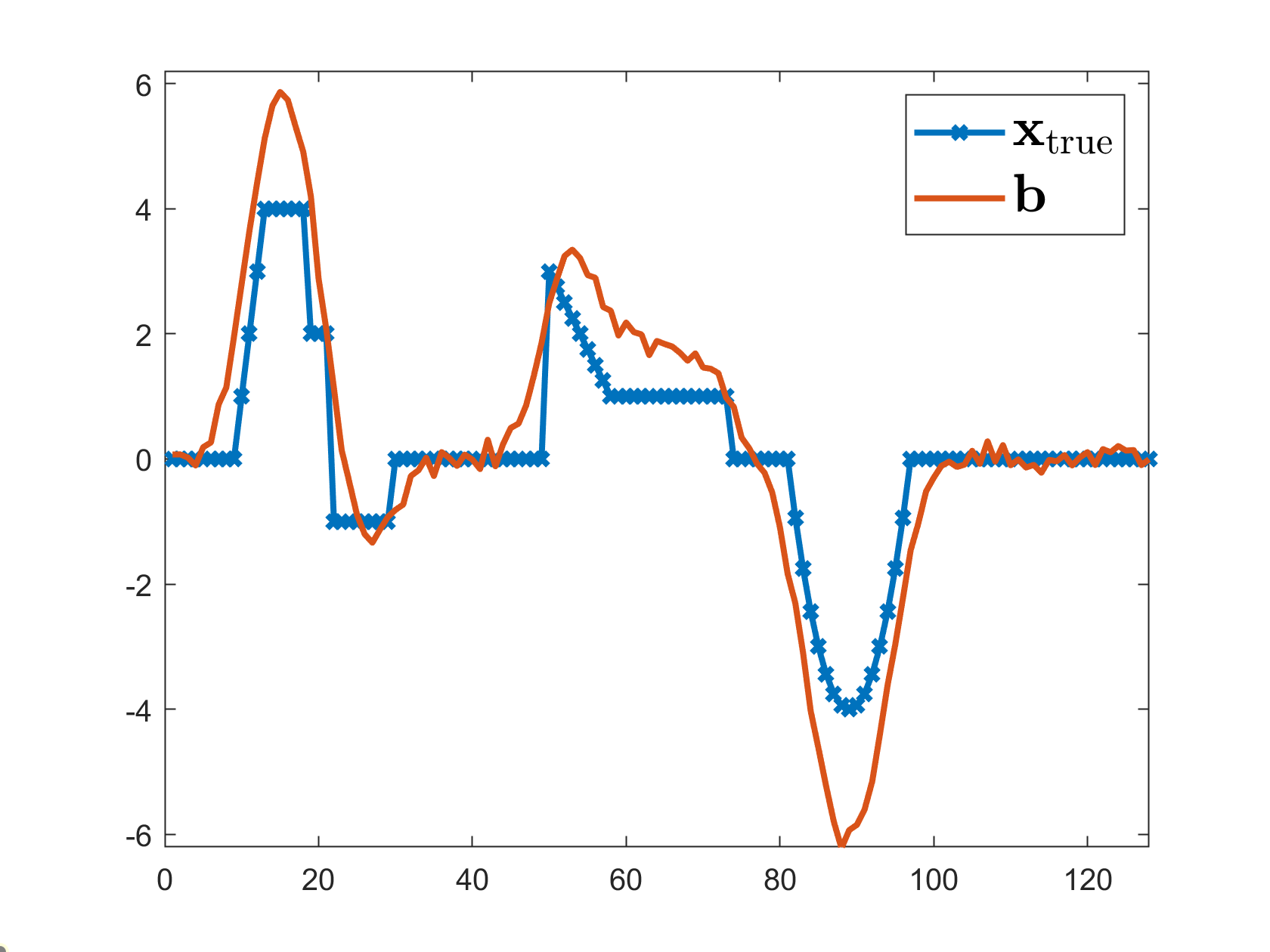
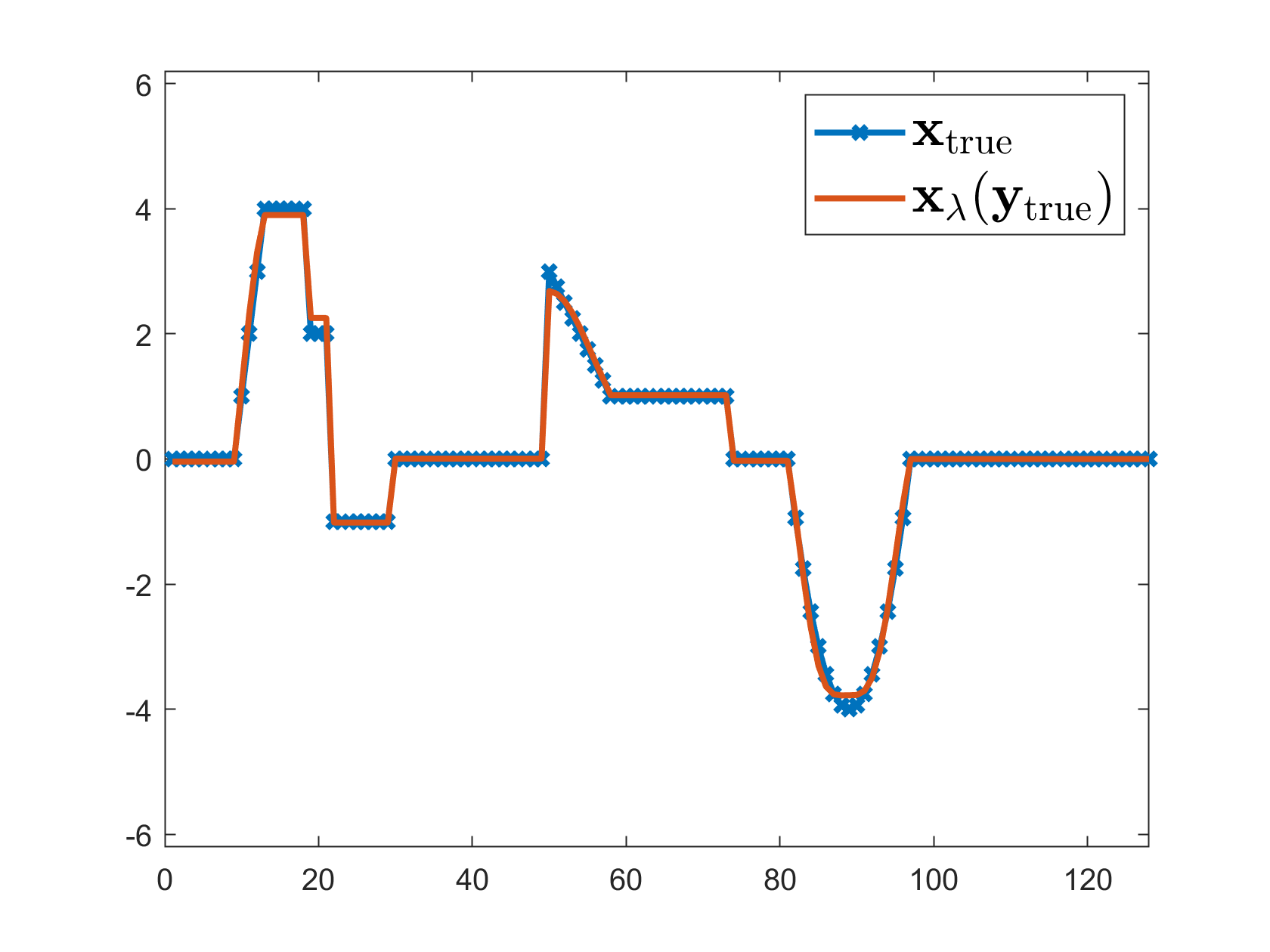
Figure 1: Convergence curves of the GenVarPro (GP) and Inexact-GenVarPro method with different tolerances: 1) $\varepsilon^{(k)}=\varepsilon^{(0)}$ (LSQR-b), 2) $\varepsilon^{(k)}=\varepsilon^{(0)}/k$ (LSQR-lb), 3) $\varepsilon^{(k)}=\varepsilon^{(k-1)}/2$ (LSQR-ab), and 4) $\varepsilon^{(k)} = 10^{-11}$ (LSQR-s).

The primary focus is on extending the VarPro method for tackling regularized problems using the Gauss-Newton method framework. VarPro effectively removes the linear variable, creating a reduced problem that can be solved more efficiently. The reduced problem involves minimizing a function related only to the nonlinear variables, potentially streamlining the convergence process. The challenges addressed include ensuring the accuracy of Jacobian approximations through iterative solvers like LSQR, especially within computationally extensive settings.

Inexact-GenVarPro Method

A key contribution is the introduction of the Inexact-GenVarPro method. This algorithm iteratively approximates solutions by incorporating LSQR to solve linear subproblems, reducing computational demands considerably. The method replaces the exact computation of Jacobian matrices with approximations, allowing the use of iterative solvers with specific stopping criteria. This paper rigorously analyzes the conditions under which the proposed method converges, providing theoretical underpinnings and conditions that guarantee convergence when using approximate Jacobians.

Convergence and Numerical Analysis

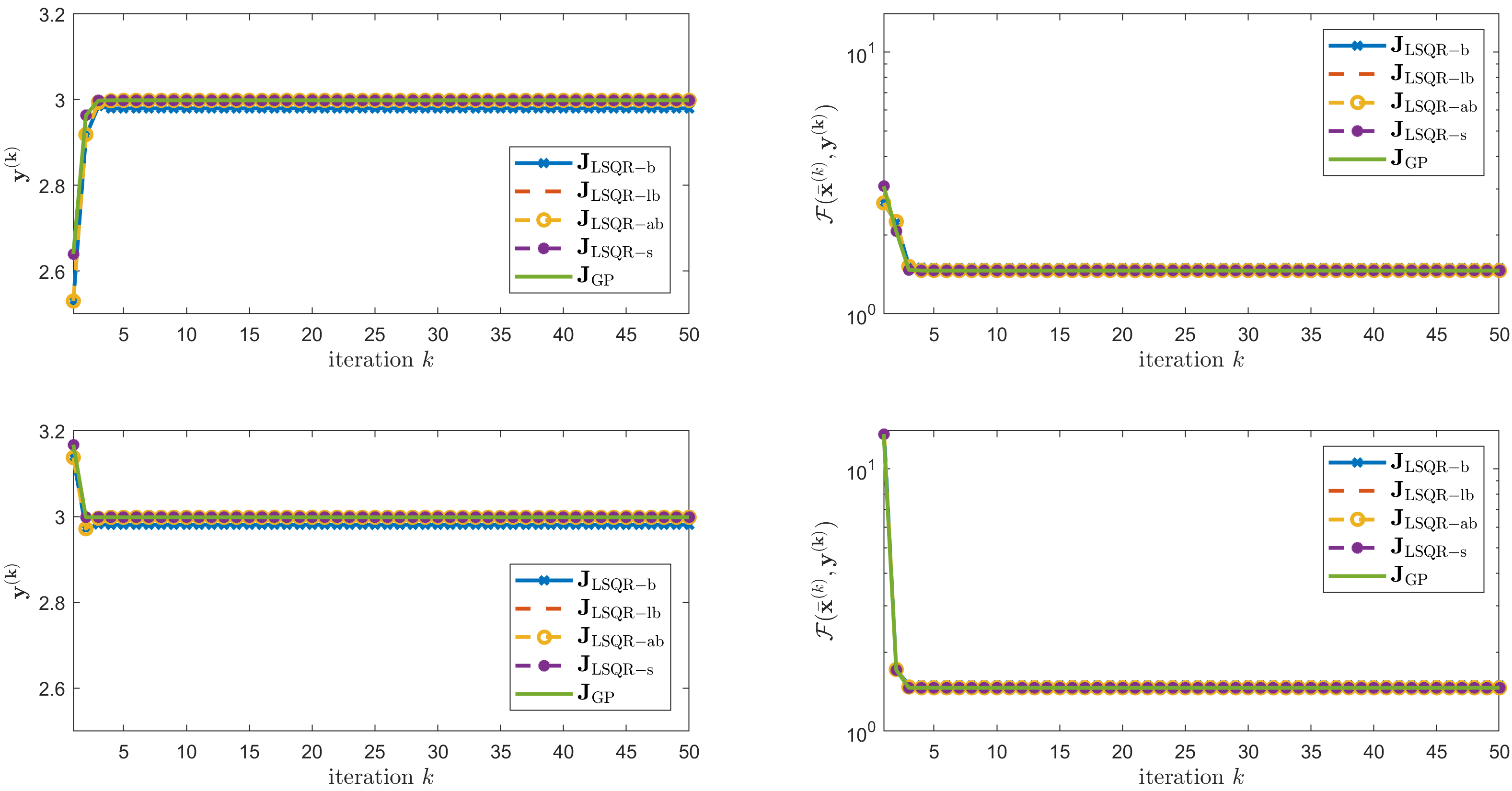
Figure 2: Distances between the solutions given at each iteration by GenVarPro ($^{(k)}$) and Inexact-GenVarPro using various tolerances.

The convergence analysis presented allows for practical implementation insights, including how initial conditions and tolerances influence convergence behavior. Numerical experiments, particularly focusing on a blind deconvolution problem, corroborate the theoretical findings with empirical evidence showing that Inexact-GenVarPro not only converges but also does so efficiently compared to the original GenVarPro method. The performance is robust against varying initial guesses for the parameters, thereby demonstrating both efficacy and flexibility.

Implications and Future Work

The findings have significant implications for large-scale inverse problem-solving, where computational efficiency is critical. By validating that iterative approximations suffice for convergence, the paper paves the way for more adaptable and resource-efficient solutions across various domains involving inverse problems. Future work involves examining the influence of choosing adaptive regularization parameters and exploring other iterative methods to expand the versatility and application scope of the proposed framework.

Conclusion

The research successfully extends the variable projection methodology to address complex, large-scale regularized inverse problems. It provides a systematic approach to managing the computational challenges associated with Jacobian calculations, offering a method that balances accuracy and computation time. This balance is particularly critical in practical applications involving high-dimensional data or situations where computational resources are limited.