Momentum-SAM: Sharpness Aware Minimization without Computational Overhead (2401.12033v2)

Abstract: The recently proposed optimization algorithm for deep neural networks Sharpness Aware Minimization (SAM) suggests perturbing parameters before gradient calculation by a gradient ascent step to guide the optimization into parameter space regions of flat loss. While significant generalization improvements and thus reduction of overfitting could be demonstrated, the computational costs are doubled due to the additionally needed gradient calculation, making SAM unfeasible in case of limited computationally capacities. Motivated by Nesterov Accelerated Gradient (NAG) we propose Momentum-SAM (MSAM), which perturbs parameters in the direction of the accumulated momentum vector to achieve low sharpness without significant computational overhead or memory demands over SGD or Adam. We evaluate MSAM in detail and reveal insights on separable mechanisms of NAG, SAM and MSAM regarding training optimization and generalization. Code is available at https://github.com/MarlonBecker/MSAM.

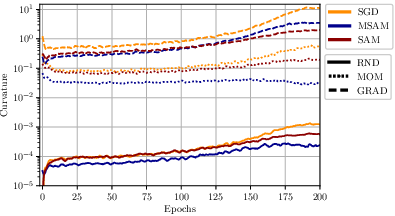
• The paper introduces a momentum-based perturbation strategy to reduce sharpness in loss landscapes without extra computational overhead.
• It employs Nesterov Accelerated Gradient to efficiently guide optimization, achieving competitive results on benchmarks like CIFAR100 and ImageNet.
• Experimental results show MSAM attains similar accuracy to SAM with roughly half the runtime, highlighting its practical efficiency.

Momentum-SAM: Sharpness Aware Minimization without Computational Overhead

Momentum-SAM (MSAM) introduces a fresh approach to sharpness-aware optimization in training deep neural networks, seeking performance similar to Sharpness Aware Minimization (SAM) but with reduced computational demands. The paper proposes using momentum vectors as perturbations to guide the optimization process toward flatter regions in the loss landscape without additional computational overhead.

Algorithm and Implementation Details

MSAM leverages the Nesterov Accelerated Gradient (NAG) concept by perturbing parameters using the accumulated momentum vector instead of the local gradient, offering computational efficiency over SAM. The key innovation of MSAM is its perturbation strategy, which reduces sharpness in loss minima with a negligible increase in computational demand or memory footprint compared to standard optimizers like SGD or Adam.

Below is the pseudocode implementation of MSAM:

Algorithm MSAM: Input: training data S, momentum μ, learning rate η, perturbation strength ρ Initialize: weights w̃₀ = random, momentum vector v₀ = 0 For t = 0 to T: sample batch Bt ⊂ S L(Bt, w̃t) = 1/|Bt| ∑ (x, y)∈Bt l(w̃t, x, y) // perturbed forward pass gt_MSAM = ∇L(Bt, w̃t) // perturbed backward pass wt = w̃t + ρ(vt / ||vt||) // remove last perturbation vt₁ = μvt + gt_MSAM // update momentum vector wt₁ = wt - η vt₁ // SGD step w̃t₁ = wt₁ - ρ(vt₁ / ||vt₁||) // perturb for next iteration

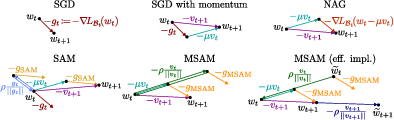
Figure 1: SGD with Momentum-SAM (MSAM; efficient implementation)

Comparative Analysis and Results

Experiments conducted on image classification benchmarks like CIFAR100 and ImageNet demonstrate MSAM's superior efficiency. For example, MSAM yields competitive accuracy compared to SAM across several architectures like WideResNet and ResNet with only half the computational time, validating its practical utility:

• WideResNet-28-10 on CIFAR100: MSAM achieves 83.31% while SAM reaches 84.16%, but with twice the runtime.
• ViT-S/32 on ImageNet: When matched for computational budget, MSAM outperforms SAM, showing a test accuracy of 70.1% versus 69.1%.

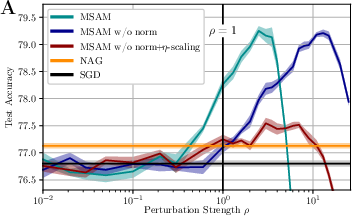
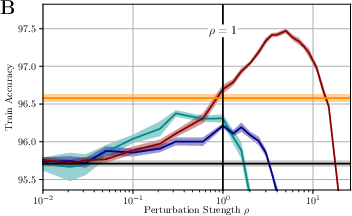
Figure 2: Test (A) and train (B) accuracy for WideResNet-16-4 on CIFAR100 for different normalization schemes of MSAM in dependence on rho. MSAM without normalization works equally well. If the perturbation epsilon is scaled by learning rate eta train performance (optimization) is increased while test performance (generalization) benefits only marginally.

Alternative Strategies and Theoretical Insights

The paper discusses various perturbation approaches, comparing MSAM's momentum-based strategy against random and last-gradient perturbations. MSAM consistently demonstrates superior performance, highlighting the efficacy of utilizing the momentum direction for sharpness estimation:

• Gradient and momentum directions show high curvatures, validating MSAM's direction choice for perturbation.
• MSAM proves effective in reducing sharpness along random perturbation directions, sometimes even outperforming SAM in this aspect.

  Figure 3: Curvature of random directions (RND), momentum (MOM) and gradient (GRAD) for different optimizers.

Moreover, the theoretical foundations draw parallels to existing sharpness theories, providing bounds that mirror SAM's guarantees but with momentum-based perturbations.

Implications and Future Directions

MSAM presents a substantial advance in optimizing neural networks for generalization while maintaining computational efficiency. The findings suggest potential for further exploration of perturbation methods and the scheduling of perturbation strengths—particularly in models like ViTs, where perturbation management during the warm-up phase significantly affects outcomes.

In conclusion, Momentum-SAM offers an optimal balance of efficiency and performance, opening avenues for resource-constrained applications and further enhancements in sharpness-aware training regimes. Future research may focus on refining perturbation scaling and timing strategies to leverage the full potential of these optimization advances across diverse neural architectures.