Papers
Topics
Authors
Recent
Gemini 2.5 Flash
Gemini 2.5 Flash
125 tokens/sec
GPT-4o
53 tokens/sec
Gemini 2.5 Pro Pro
42 tokens/sec
o3 Pro
4 tokens/sec
GPT-4.1 Pro
47 tokens/sec
DeepSeek R1 via Azure Pro
28 tokens/sec
2000 character limit reached

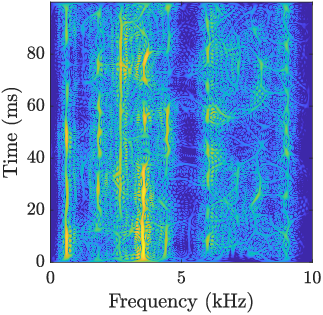
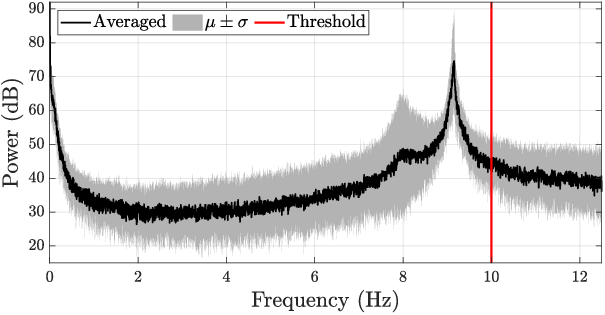
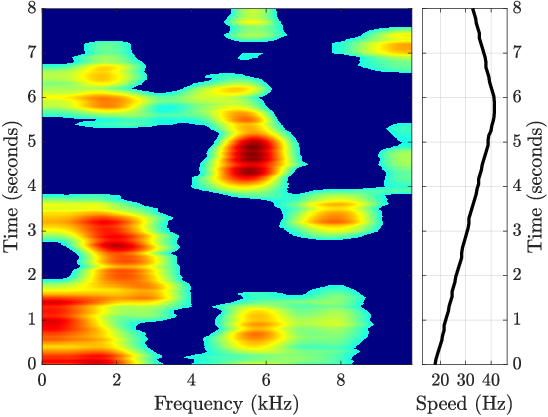
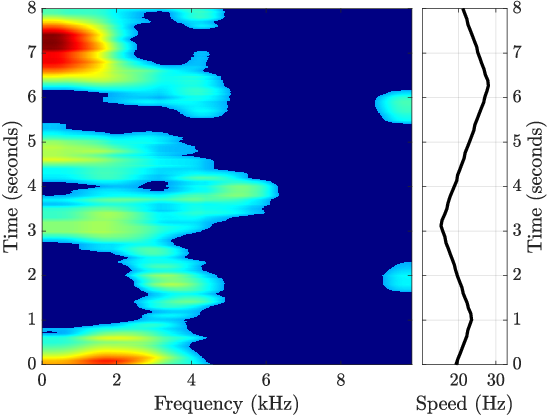
Quadratic Time-Frequency Analysis of Vibration Signals for Diagnosing Bearing Faults (2401.01172v2)

Published 2 Jan 2024 in cs.LG, cs.AI, cs.SY, and eess.SY

Abstract: Diagnosis of bearing faults is paramount to reducing maintenance costs and operational breakdowns. Bearing faults are primary contributors to machine vibrations, and analyzing their signal morphology offers insights into their health status. Unfortunately, existing approaches are optimized for controlled environments, neglecting realistic conditions such as time-varying rotational speeds and the vibration's non-stationary nature. This paper presents a fusion of time-frequency analysis and deep learning techniques to diagnose bearing faults under time-varying speeds and varying noise levels. First, we formulate the bearing fault-induced vibrations and discuss the link between their non-stationarity and the bearing's inherent and operational parameters. We also elucidate quadratic time-frequency distributions and validate their effectiveness in resolving distinctive dynamic patterns associated with different bearing faults. Based on this, we design a time-frequency convolutional neural network (TF-CNN) to diagnose various faults in rolling-element bearings. Our experimental findings undeniably demonstrate the superior performance of TF-CNN in comparison to recently developed techniques. They also assert its versatility in capturing fault-relevant non-stationary features that couple with speed changes and show its exceptional resilience to noise, consistently surpassing competing methods across various signal-to-noise ratios and performance metrics. Altogether, the TF-CNN achieves substantial accuracy improvements up to 15%, in severe noise conditions.

Definition Search Book Streamline Icon: https://streamlinehq.com
References (50)
  1. O. AlShorman, M. Irfan, N. Saad, D. Zhen, N. Haider, A. Glowacz, and A. AlShorman, “A Review of Artificial Intelligence Methods for Condition Monitoring and Fault Diagnosis of Rolling Element Bearings for Induction Motor,” Shock and Vibration, vol. 2020, DOI 10.1155/2020/8843759, p. 8843759, 2020.
  2. A. Rai and S. H. Upadhyay, “A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings,” Tribology International, vol. 96, DOI 10.1016/j.triboint.2015.12.037, pp. 289–306, 2016.
  3. K. C. Deekshit Kompella, M. Venu Gopala Rao, and R. Srinivasa Rao, “Bearing fault detection in a 3 phase induction motor using stator current frequency spectral subtraction with various wavelet decomposition techniques,” Ain Shams Engineering Journal, vol. 9, DOI 10.1016/j.asej.2017.06.002, no. 4, pp. 2427–2439, 2018.
  4. T. Jalonen, M. Al-Sa’d, S. Kiranyaz, and M. Gabbouj, “Real-Time Vibration-Based Bearing Fault Diagnosis Under Time-Varying Speed Conditions,” arXiv, DOI 10.48550/arXiv.2311.18547, 2023.
  5. T. Ince, J. Malik, O. C. Devecioglu, S. Kiranyaz, O. Avci, L. Eren, and M. Gabbouj, “Early Bearing Fault Diagnosis of Rotating Machinery by 1D Self-Organized Operational Neural Networks,” IEEE Access, vol. 9, DOI 10.1109/ACCESS.2021.3117603, pp. 139 260–139 270, 2021.
  6. A. Youcef Khodja, N. Guersi, M. N. Saadi, and N. Boutasseta, “Rolling element bearing fault diagnosis for rotating machinery using vibration spectrum imaging and convolutional neural networks,” The International Journal of Advanced Manufacturing Technology, vol. 106, DOI 10.1007/s00170-019-04726-7, pp. 1737–1751, 2020.
  7. C. Malla and I. Panigrahi, “Review of Condition Monitoring of Rolling Element Bearing Using Vibration Analysis and Other Techniques,” Journal of Vibration Engineering & Technologies, vol. 7, DOI 10.1007/s42417-019-00119-y, no. 4, pp. 407–414, 2019.
  8. T. Ince, S. Kiranyaz, L. Eren, M. Askar, and M. Gabbouj, “Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks,” IEEE Transactions on Industrial Electronics, vol. 63, DOI 10.1109/TIE.2016.2582729, no. 11, pp. 7067–7075, 2016.
  9. L. Eren, T. Ince, and S. Kiranyaz, “A Generic Intelligent Bearing Fault Diagnosis System Using Compact Adaptive 1D CNN Classifier,” Journal of Signal Processing Systems, vol. 91, DOI 10.1007/s11265-018-1378-3, no. 2, pp. 179–189, 2019.
  10. O. Abdeljaber, S. Sassi, O. Avci, S. Kiranyaz, A. A. Ibrahim, and M. Gabbouj, “Fault Detection and Severity Identification of Ball Bearings by Online Condition Monitoring,” IEEE Transactions on Industrial Electronics, vol. 66, DOI 10.1109/TIE.2018.2886789, no. 10, pp. 8136–8147, 2019.
  11. T. Jalonen, M. Al-Sa’d, R. Mellanen, S. Kiranyaz, and M. Gabbouj, “Real-Time Damage Detection in Fiber Lifting Ropes Using Convolutional Neural Networks,” arXiv, DOI 10.48550/arXiv.2302.11947, 2023.
  12. Z. Jiang, K. Zhang, L. Xiang, G. Yu, and Y. Xu, “A time-frequency spectral amplitude modulation method and its applications in rolling bearing fault diagnosis,” Mechanical Systems and Signal Processing, vol. 185, DOI 10.1016/j.ymssp.2022.109832, p. 109832, 2023.
  13. A. Prudhom, J. Antonino-Daviu, H. Razik, and V. Climente-Alarcon, “Time-frequency vibration analysis for the detection of motor damages caused by bearing currents,” Mechanical Systems and Signal Processing, vol. 84, DOI 10.1016/j.ymssp.2015.12.008, pp. 747–762, 2017.
  14. X. Zhang, Z. Liu, J. Wang, and J. Wang, “Time–frequency analysis for bearing fault diagnosis using multiple Q-factor Gabor wavelets,” ISA Transactions, vol. 87, DOI 10.1016/j.isatra.2018.11.033, pp. 225–234, 2019.
  15. I. Attoui, N. Fergani, N. Boutasseta, B. Oudjani, and A. Deliou, “A new time–frequency method for identification and classification of ball bearing faults,” Journal of Sound and Vibration, vol. 397, DOI 10.1016/j.jsv.2017.02.041, pp. 241–265, 2017.
  16. G. Tang, Y. Wang, Y. Huang, and H. Wang, “Multiple Time-Frequency Curve Classification for Tacho-Less and Resampling-Less Compound Bearing Fault Detection Under Time-Varying Speed Conditions,” IEEE Sensors Journal, vol. 21, DOI 10.1109/JSEN.2020.3035623, no. 4, pp. 5091–5101, 2021.
  17. Z. Feng, M. Liang, and F. Chu, “Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples,” Mechanical Systems and Signal Processing, vol. 38, DOI 10.1016/j.ymssp.2013.01.017, no. 1, pp. 165–205, 2013, condition monitoring of machines in non-stationary operations.
  18. D. Zhang and Z. Feng, “Enhancement of time-frequency post-processing readability for nonstationary signal analysis of rotating machinery: Principle and validation,” Mechanical Systems and Signal Processing, vol. 163, DOI 10.1016/j.ymssp.2021.108145, p. 108145, 2022.
  19. S. Rajagopalan, J. A. Restrepo, J. M. Aller, T. G. Habetler, and R. G. Harley, “Nonstationary Motor Fault Detection Using Recent Quadratic Time–Frequency Representations,” IEEE Transactions on Industry Applications, vol. 44, DOI 10.1109/TIA.2008.921431, no. 3, pp. 735–744, 2008.
  20. M. Al-Sa’d, “Time-Frequency Analysis: Application to Electroencephalogram Signal Processing,” Ph.D. dissertation, Tampere University, 2022. [Online]. Available: https://urn.fi/URN:ISBN:978-952-03-2503-9
  21. F. Auger, P. Flandrin, Y.-T. Lin, S. McLaughlin, S. Meignen, T. Oberlin, and H.-T. Wu, “Time-Frequency Reassignment and Synchrosqueezing: An Overview,” IEEE Signal Processing Magazine, vol. 30, DOI 10.1109/MSP.2013.2265316, no. 6, pp. 32–41, 2013.
  22. M. Al-Sa’d, B. Boashash, and M. Gabbouj, “Design of an Optimal Piece-Wise Spline Wigner-Ville Distribution for TFD Performance Evaluation and Comparison,” IEEE Transactions on Signal Processing, vol. 69, DOI 10.1109/TSP.2021.3089291, pp. 3963–3976, 2021.
  23. H. Dong, G. Yu, and Q. Jiang, “Time–Frequency-Multisqueezing Transform,” IEEE Transactions on Industrial Electronics, vol. 71, DOI 10.1109/TIE.2023.3279518, no. 4, pp. 4151–4161, 2024.
  24. J. Cai and Y. Xiao, “Time-frequency analysis method of bearing fault diagnosis based on the generalized S transformation,” Journal of Vibroengineering, vol. 19, DOI 10.21595/jve.2017.18244, no. 6, pp. 4221–4230, Sep. 2017.
  25. L. Wang, J. Xiang, and Y. Liu, “A time–frequency-based maximum correlated kurtosis deconvolution approach for detecting bearing faults under variable speed conditions,” Measurement Science and Technology, vol. 30, DOI 10.1088/1361-6501/ab3678, no. 12, p. 125005, Sep. 2019.
  26. Y. Zhang, K. Xing, R. Bai, D. Sun, and Z. Meng, “An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image,” Measurement, vol. 157, DOI 10.1016/j.measurement.2020.107667, p. 107667, 2020.
  27. S. Li, W. Yang, A. Zhang, H. Liu, J. Huang, C. Li, and J. Hu, “A Novel Method of Bearing Fault Diagnosis in Time-Frequency Graphs Using InceptionResnet and Deformable Convolution Networks,” IEEE Access, vol. 8, DOI 10.1109/ACCESS.2020.2995198, pp. 92 743–92 753, 2020.
  28. Y. Kaya, F. Kuncan, and H. Ertunç, “A new automatic bearing fault size diagnosis using time-frequency images of CWT and deep transfer learning methods,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 30, DOI 10.55730/1300-0632.3909, no. 5, pp. 1851–1867, 2022.
  29. Z. Chen, J. Cen, and J. Xiong, “Rolling Bearing Fault Diagnosis Using Time-Frequency Analysis and Deep Transfer Convolutional Neural Network,” IEEE Access, vol. 8, DOI 10.1109/ACCESS.2020.3016888, pp. 150 248–150 261, 2020.
  30. R. Wang, J. Zhang, H. Fang, L. Yu, and J. Chen, “Sparsity enforced time–frequency decomposition in the Bayesian framework for bearing fault feature extraction under time-varying conditions,” Mechanical Systems and Signal Processing, vol. 185, DOI 10.1016/j.ymssp.2022.109755, p. 109755, 2023.
  31. G. Yu, “A Concentrated Time–Frequency Analysis Tool for Bearing Fault Diagnosis,” IEEE Transactions on Instrumentation and Measurement, vol. 69, DOI 10.1109/TIM.2019.2901514, no. 2, pp. 371–381, 2020.
  32. I. Quinde, J. Sumba, L. Ochoa, A. J. Guevara, and R. Morales-Menendez, “Bearing Fault Diagnosis Based on Optimal Time-Frequency Representation Method,” IFAC-PapersOnLine, vol. 52, DOI 10.1016/j.ifacol.2019.09.140, no. 11, pp. 194–199, 2019, 5th IFAC Conference on Intelligent Control and Automation Sciences ICONS 2019.
  33. J. Wang, Z. Mo, H. Zhang, and Q. Miao, “A Deep Learning Method for Bearing Fault Diagnosis Based on Time-Frequency Image,” IEEE Access, vol. 7, DOI 10.1109/ACCESS.2019.2907131, pp. 42 373–42 383, 2019.
  34. G. Dong and J. Chen, “Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings,” Mechanical Systems and Signal Processing, vol. 33, DOI 10.1016/j.ymssp.2012.06.008, pp. 212–236, 2012.
  35. A. Vitor, A. Goedtel, M. F. Castoldi, W. A. Souza, and G. H. Bazan, “Induction Machine Fault Diagnosis With Quadratic Time–Frequency Distributions: State of the Art,” IEEE Transactions on Instrumentation and Measurement, vol. 72, DOI 10.1109/TIM.2023.3323999, pp. 1–16, 2023.
  36. A. Kumar and R. Kumar, “Role of Signal Processing, Modeling and Decision Making in the Diagnosis of Rolling Element Bearing Defect: A Review,” Journal of Nondestructive Evaluation, vol. 38, DOI 10.1007/s10921-018-0543-8, no. 1, p. 5, 2018.
  37. N. Sawalhi and R. B. Randall, “Vibration response of spalled rolling element bearings: Observations, simulations and signal processing techniques to track the spall size,” Mechanical Systems and Signal Processing, vol. 25, DOI 10.1016/j.ymssp.2010.09.009, no. 3, pp. 846–870, 2011.
  38. “Rolling element bearing schematic.” [Online]. Available: https://upload.wikimedia.org/wikipedia/commons/f/f6/HARP_bearing.jpg
  39. S. Kim, D. An, and J.-H. Choi, “Diagnostics 101: A Tutorial for Fault Diagnostics of Rolling Element Bearing Using Envelope Analysis in MATLAB,” Applied Sciences, vol. 10, DOI 10.3390/app10207302, no. 20, 2020.
  40. Z. Feng, X. Chen, and T. Wang, “Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions,” Journal of Sound and Vibration, vol. 400, DOI 10.1016/j.jsv.2017.03.037, pp. 71–85, 2017.
  41. H. Saruhan, S. Saridemir, A. Qicek, and I. Uygur, “Vibration analysis of rolling element bearings defects,” Journal of applied research and technology, vol. 12, DOI 10.1016/S1665-6423(14)71620-7, no. 3, pp. 384–395, 2014.
  42. H. Cheng, Y. Zhang, W. Lu, and Z. Yang, “Research on ball bearing model based on local defects,” SN Applied Sciences, vol. 1, DOI 10.1007/s42452-019-1251-4, no. 10, p. 1219, 2019.
  43. X. Zhang, Q. Han, Z. Peng, and F. Chu, “A new nonlinear dynamic model of the rotor-bearing system considering preload and varying contact angle of the bearing,” Communications in Nonlinear Science and Numerical Simulation, vol. 22, DOI 10.1016/j.cnsns.2014.07.024, no. 1, pp. 821–841, 2015.
  44. B. Boashash, A. A. El-Bey, and M. F. Al-Sa’d, “Multisensor Time–Frequency Signal Processing MATLAB package: An analysis tool for multichannel non-stationary data,” SoftwareX, vol. 8, DOI 10.1016/j.softx.2017.12.002, pp. 53–58, 2018, digital Signal Processing & SoftwareX - Joint Special Issue on Reproducible Research in Signal Processing.
  45. W. Jung, S.-H. Kim, S.-H. Yun, J. Bae, and Y.-H. Park, “Vibration, acoustic, temperature, and motor current dataset of rotating machine under varying operating conditions for fault diagnosis,” Data in brief, vol. 48, DOI 10.1016/j.dib.2023.109049, pp. 109 049–109 049, 2023.
  46. Q. Ni, J. C. Ji, B. Halkon, K. Feng, and A. K. Nandi, “Physics-Informed Residual Network (PIResNet) for rolling element bearing fault diagnostics,” Mechanical Systems and Signal Processing, vol. 200, DOI 10.1016/j.ymssp.2023.110544, p. 110544, 2023.
  47. L. van der Maaten and G. Hinton, “Visualizing data using t-SNE,” Journal of Machine Learning Research, vol. 9, no. 86, pp. 2579–2605, 2008.
  48. R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam, D. Parikh, and D. Batra, “Grad-CAM: Visual Explanations From Deep Networks via Gradient-Based Localization,” in Proceedings of the IEEE International Conference on Computer Vision (ICCV), pp. 618–626, Oct. 2017.
  49. S. Kiranyaz, T. Ince, A. Iosifidis, and M. Gabbouj, “Operational neural networks,” Neural Computing and Applications, vol. 32, DOI 10.1007/s00521-020-04780-3, no. 11, pp. 6645–6668, 2020.
  50. S. Kiranyaz, J. Malik, H. B. Abdallah, T. Ince, A. Iosifidis, and M. Gabbouj, “Self-organized Operational Neural Networks with Generative Neurons,” Neural Networks, vol. 140, DOI 10.1016/j.neunet.2021.02.028, pp. 294–308, 2021.

Summary

We haven't generated a summary for this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Summarize Now