Hyperparameter Optimization for Large Language Model Instruction-Tuning (2312.00949v2)

Abstract: The fine-tuning of LLMs has enabled them to recently achieve milestones in natural language processing applications. The emergence of ever larger LLMs has paved the way for more efficient fine-tuning methods. Among these, the Low-Rank Adaptation (LoRA) method keeps most of the weights of the pre-trained LLM frozen while introducing a low-rank decomposition of the weight matrix, enabling the tuning of only a very small proportion of the network. The performance on downstream tasks of models fine-tuned with LoRA heavily relies on a set of hyperparameters including the rank of the decomposition. In this work, we investigate the choice of these hyperparameters through two main blackbox optimization (BBO) techniques. We examine the whole pipeline of performing fine-tuning and validation on a pre-trained LLM as a blackbox and efficiently explore the space of hyperparameters with the \nomad algorithm, achieving a boost in performance and human alignment of the tuned model.

• The paper formulates hyperparameter optimization for instruction-tuning as a blackbox optimization problem, comparing NOMAD/MADS and TPE approaches.
• It demonstrates that optimized low-rank LoRA configurations can rival high-rank setups while offering memory efficiency and faster inference.
• The study highlights the gap between proxy validation loss and downstream performance, advocating for multi-objective HPO in LLM tuning.

Hyperparameter Optimization for Instruction-Tuned LLMs

Introduction and Context

Instruction-tuning of LLMs, wherein pretrained generative models are further adapted using human-written instruction-response pairs, has become the standard approach for improving alignment and downstream generalization capabilities. However, given the scale of models (billions of parameters) and the complexity of instruction datasets, full-parameter fine-tuning is intractable for most practitioners. Parameter Efficient Fine-Tuning (PEFT) methods, particularly Low-Rank Adaptation (LoRA), mitigate the computational and memory challenges by updating only a small subset of induced low-rank matrices, leaving most of the pretrained backbone frozen. The actual performance of instruction-tuned LLMs under PEFT, however, depends critically on a set of hyperparameters that govern the adaptation, including the LoRA rank, the scaling factor ($\alpha$), learning rate, and dropout.

The paper systematically frames hyperparameter optimization (HPO) for LoRA-based instruction-tuning as a blackbox optimization (BBO) problem. The authors provide a comparative empirical paper of two distinct BBO paradigms—direct search using the mesh adaptive direct search (MADS) algorithm (as in NOMAD) and model-based Bayesian optimization via the tree-structured Parzen estimator (TPE, as implemented in NNI)—applied to the HPO outer loop of supervised LoRA fine-tuning. They demonstrate the strong dependence of best-performing models on the choice of HPO method and on the HPO search space. Their paper reveals nontrivial tradeoffs in model generalization and user-alignment, and provides a principled reference for practitioners seeking to automate and systematize the HPO workflow for instruction-tuned LLMs.

Methodological Framework

Parameter-Efficient Instruction-Tuning and HPO Search Space

The tuning pipeline employs LLaMA 2–7B as the backbone and optimizes LoRA's hyperparameter configuration by searching over LoRA rank ($r \in [1, 512]$), scaling ($\alpha$), dropout, and learning rate. Two instruction datasets (Alpaca, Dolly) are merged, balancing domain diversity and response heterogeneity. Fine-tuning is conducted via the HuggingFace Transformers API with AdamW optimizer on A100 GPUs, and validation loss after each evaluation serves as the single-objective metric for the BBO solvers.

Blackbox Optimization Algorithms

• NOMAD/MADS: Mesh Adaptive Direct Search, a model-free direct search approach with rigorous hierarchical convergence guarantees, generates candidate hyperparameter configurations by iteratively applying poll and search steps over an adaptive discretized mesh.
• NNI-TPE: The tree-structured Parzen estimator, a model-based Bayesian optimizer, uses density estimation and acquisition-driven exploration/exploitation for sequential selection, with models fit and updated after each batch of evaluations.

Both methods are run under tight computational budgets, with NOMAD/MADS initialized via cache-warm start from prior runs.

Empirical Results and Analysis

Optimization Rounds and Search Behavior

Initial experiments (NOMAD, 50 evals, $r \leq 128$) reveal that, under a small evaluation budget, the algorithm tends to select high LoRA ranks ($r=128$ upper bound), and performance plateaus quickly as a function of training epochs. The second-round experiments expand the search space ($r \leq 512$) and increase the budget (100 evals), now comparing both NOMAD and NNI-TPE.

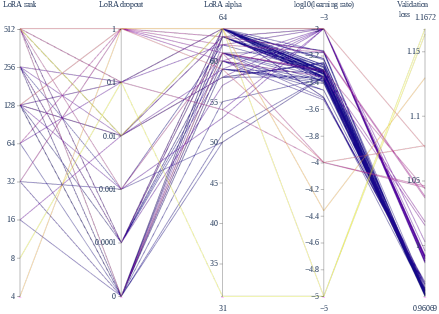
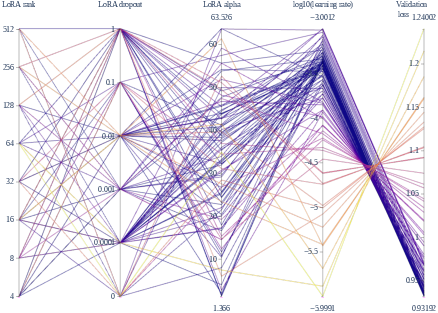
Figure 1: Parallel coordinate visualization of the second-round hyperparameter exploration, with lower loss trials emphasized. This reveals distinct search dynamics between NOMAD and NNI-TPE, with nominally higher ranks favored by NOMAD and a broader exploration (including lower ranks) by TPE.

A key empirical finding is that:

• NOMAD/MADS predominantly identifies optimal configurations in the high-rank regime ($r=256, 512$), maximizing performance by maximizing LoRA's adaptation subspace.
• NNI-TPE, in contrast, achieves comparable or lower validation loss with markedly lower ranks ($r=8$ in the best run), but with substantially greater exploration of the search space.

This demonstrates that low-rank LoRA configurations, if properly matched with other hyperparameters, can achieve validation losses that are competitive with or outperform high-rank runs—contradicting the common heuristic that "larger is always better" for LoRA rank in instruction-tuning.

Downstream Generalization and Human Preference

Models selected purely by low validation loss do not always correspond to globally best downstream metrics on tasks such as MMLU, BBH, DROP, and HumanEval. The top 10 models from each optimizer significantly outperform default or no-fine-tuning baselines on MMLU and HumanEval, but not universally on tasks such as DROP and BBH. Notably, the best validation loss model is not the model with the best aggregate downstream scores, indicating a lack of perfect alignment between proxy loss and actual task generalization.

In addition to automatic evaluation, human preference is directly measured on the Vicuna multi-turn dialog dataset. Human annotators consistently prefer outputs from HPO-optimized models over those fine-tuned with heuristic/default LoRA hyperparameters, with a preference margin of 5%.

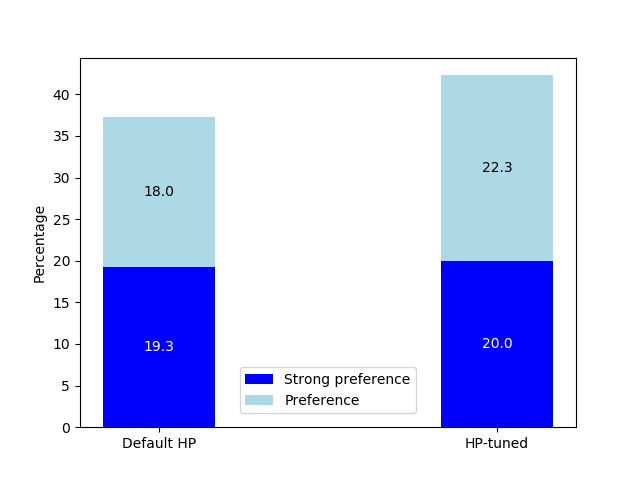
Figure 2: Human evaluation outcomes on the Vicuna dataset comparing models optimized by HPO against default-hyperparameter baselines; HPO-tuned models consistently win direct pairwise comparisons.

Discussion: Practical Implications and Theoretical Insights

1. Robustness of HPO for PEFT: The results establish that low-rank LoRA, when optimized in the context of other hyperparameters, can deliver equivalent or better performance than high-rank configurations while offering substantial gains in memory efficiency and inference-time speedup. This has direct implications for resource-constrained deployment scenarios and for practitioners seeking cost-effective fine-tuning regimes.
2. Algorithmic Complementarity in BBO: NOMAD/MADS (direct search) and TPE (Bayesian optimization) display orthogonal exploration patterns. For hyperparameter landscapes with intricate non-separabilities or ruggedness, direct search methods may avoid overcommitment to potentially misleading surrogate models; conversely, model-based methods like TPE enable exploitation of local minima that model-free methods may miss, especially under tight evaluation budgets.
3. Proxy Validation Loss as an Imperfect Objective: Aggressively minimizing validation loss on held-out instructions does not guarantee Pareto-optimality across diverse downstream tasks. Incorporating explicit multi-objective optimization and auxiliary metrics (e.g., agreement with human preference, diversity/robustness) into the BBO formulation would increase the fidelity of HPO to real-world task requirements.
4. Outer-loop HPO as Canonical in LLM Tuning: Given the magnitude of possible gains, the paper provides strong evidence that automated HPO should always constitute the outer loop of supervised LLM fine-tuning workflows for any novel combination of base model, PEFT method, and instruction data. Manual hyperparameter choices, even if empirically "reasonable," leave significant performance on the table both in task generalization and user alignment.

Conclusion

The paper provides an end-to-end demonstration that automated HPO via blackbox optimization algorithms yields robust and substantial improvements in the performance of LoRA-based, instruction-tuned LLMs. The observed diversity of effective hyperparameter configurations across BBO methods and search regimes emphasizes the complexity of the HPO landscape, with no single heuristic universally optimal. The work motivates future research into multi-objective blackbox optimization for instruction tuning, as well as systematic investigation of the inductive biases of different HPO algorithms in high-dimensional, expensive-to-evaluate LLM fine-tuning problems. In practice, formalizing HPO as an outer loop with rigorous BBO/SMBO solvers should be the default structure for scalable and effective LLM deployment.