Combinatorial Optimization with Policy Adaptation using Latent Space Search (2311.13569v2)

Abstract: Combinatorial Optimization underpins many real-world applications and yet, designing performant algorithms to solve these complex, typically NP-hard, problems remains a significant research challenge. Reinforcement Learning (RL) provides a versatile framework for designing heuristics across a broad spectrum of problem domains. However, despite notable progress, RL has not yet supplanted industrial solvers as the go-to solution. Current approaches emphasize pre-training heuristics that construct solutions but often rely on search procedures with limited variance, such as stochastically sampling numerous solutions from a single policy or employing computationally expensive fine-tuning of the policy on individual problem instances. Building on the intuition that performant search at inference time should be anticipated during pre-training, we propose COMPASS, a novel RL approach that parameterizes a distribution of diverse and specialized policies conditioned on a continuous latent space. We evaluate COMPASS across three canonical problems - Travelling Salesman, Capacitated Vehicle Routing, and Job-Shop Scheduling - and demonstrate that our search strategy (i) outperforms state-of-the-art approaches on 11 standard benchmarking tasks and (ii) generalizes better, surpassing all other approaches on a set of 18 procedurally transformed instance distributions.

• The paper introduces COMPASS, an RL framework that conditions policies on latent space vectors to diversify solution strategies in combinatorial optimization.
• It employs an evolutionary strategy (CMA-ES) during inference to dynamically search the latent space, achieving state-of-the-art results on TSP, CVRP, and JSSP.
• The method improves generalization and scalability, offering practical insights for adapting policies in complex, real-world optimization scenarios.

Combinatorial Optimization with Policy Adaptation using Latent Space Search

Introduction

The field of combinatorial optimization (CO) involves finding optimal configurations of discrete variables under specific constraints, a class of problems often characterized by their NP-hard nature. Although industrial solvers are traditionally used for such tasks, reinforcement learning (RL) proposes a flexible framework for developing heuristic approaches. Despite advancements, existing RL techniques have not effectively replaced conventional solvers. One area identified for improvement is in the generalization capabilities of policies utilized during inference, which current models often inadequately address due to their reliance on pre-defined solutions that lack dynamic adaptability.

COMPASS Approach

COMPASS (COMbinatorial optimization with Policy Adaptation using Latent Space Search) introduces a novel RL strategy whereby policies are conditioned on vectors sampled from a latent space, allowing for a continuum of policy configurations. This framework extends beyond the traditional single-policy approach by facilitating policy specialization and diversification through its structured latent space, thereby enhancing solution generalization and effectiveness across a variety of CO problems—specifically, addressing instances both during training and out-of-distribution (OOD).

Figure 1: Our method COMPASS is composed of the following two phases. A. Training - the latent space is sampled to generate vectors that the policy can condition upon. The conditioned policies are then evaluated and only the best one is trained to create specialization within the latent space. B. Inference - at inference time the latent space is searched through an evolution strategy to exploit regions with high-performing policies for each instance.

Methodology

Latent Space and Training

The latent space is leveraged by encoding varying policies into continuous domains, notably a 16-dimensional bounded space, which fosters a multitude of specialized policies. Training encourages sections of this latent space to specialize in subspecies of problem instances, thereby creating a diverse portfolio of solutions. A key innovation in COMPASS is training only the most successful policies for given instances based on latent space sampling, ensuring that high-performance vectors are emphasized, thus promoting both diversity and specialization during the learning process.

Inference Strategy

During inference, an evolutionary strategy, specifically Covariance Matrix Adaptation Evolution Strategy (CMA-ES), is implemented to navigate and exploit the latent space effectively. This search method allows COMPASS to adapt policies on the fly by identifying high-performance areas within the latent space. The use of multiple independent CMA-ES components allows diverse exploration and exploitation of the policy space, improving the likelihood of optimal policy retrieval for novel problem spaces.

Experimental Evaluation

COMPASS was rigorously tested on three notable CO problems: the Travelling Salesman Problem (TSP), the Capacitated Vehicle Routing Problem (CVRP), and the Job-Shop Scheduling Problem (JSSP). Through comprehensive testing across standard and expanded datasets, including out-of-distribution variations created via procedural mutation operators, COMPASS consistently surpassed competing RL methods in establishing state-of-the-art performance metrics, particularly in generalization to unseen instances.

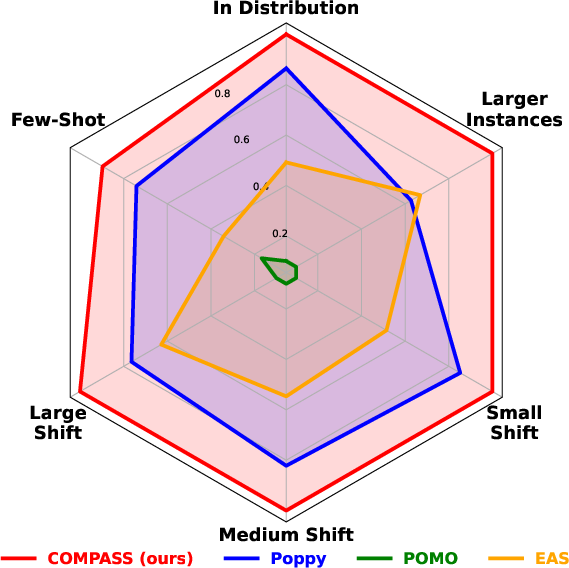
Figure 2: Performance of COMPASS and the main baselines aggregated across several tasks over three problems (TSP, CVRP, and JSSP). For each task (problem type, instance size, mutation power), we normalize values between 0 and 1 (corresponding to the worst and best performing RL method, respectively). Hence, all tasks have the same impact on the aggregated metrics. COMPASS surpasses the baselines on all of them, showing its versatility for all types of tasks and in particular, its generalization capacity.

Conclusion

COMPASS represents a significant enhancement in CO by combining a diverse, solution-space-driven policy architecture with efficient inferential search techniques. Its superior performance in both canonical and generalized tasks underscores its potential to redefine how RL approaches complexity in CO problems. Future work may explore further refinements in latent space structuring and expansion of its applicability to additional problem domains within AI.

COMPASS efficiently aligns theoretical foundations with practical implementation, offering advantages in flexibility, scalability, and performance, particularly in handling the constraints and variability intrinsic to real-world combinatorial optimization scenarios.