Multimarginal generative modeling with stochastic interpolants (2310.03695v1)

Abstract: Given a set of $K$ probability densities, we consider the multimarginal generative modeling problem of learning a joint distribution that recovers these densities as marginals. The structure of this joint distribution should identify multi-way correspondences among the prescribed marginals. We formalize an approach to this task within a generalization of the stochastic interpolant framework, leading to efficient learning algorithms built upon dynamical transport of measure. Our generative models are defined by velocity and score fields that can be characterized as the minimizers of simple quadratic objectives, and they are defined on a simplex that generalizes the time variable in the usual dynamical transport framework. The resulting transport on the simplex is influenced by all marginals, and we show that multi-way correspondences can be extracted. The identification of such correspondences has applications to style transfer, algorithmic fairness, and data decorruption. In addition, the multimarginal perspective enables an efficient algorithm for reducing the dynamical transport cost in the ordinary two-marginal setting. We demonstrate these capacities with several numerical examples.

• The paper introduces a multimarginal generative model that extends optimal transport to K+1 marginals using barycentric stochastic interpolants.
• It employs conditional expectation vector fields and optimized simplex paths to reduce transport cost and accelerate convergence in image translation tasks.
• The framework enables joint sample synthesis and emergent style transfer, supporting all-to-all mapping and enhanced content preservation across diverse domains.

Multimarginal Generative Modeling with Stochastic Interpolants

Introduction and Context

The paper “Multimarginal generative modeling with stochastic interpolants” (2310.03695) addresses the extension of dynamical generative modeling from the classical two-marginal optimal transport (OT) paradigm to arbitrary collections of $K+1$ prescribed marginals. The proposed framework generalizes the stochastic interpolant/flow matching constructions by allowing generative models to operate over the simplex of all convex combinations of a set of marginal distributions. This enables the coherent extraction of multi-way correspondences and supports new applications including all-to-all image translation, style transfer, and algorithmic fairness.

Stochastic Interpolants for Multimarginal Generation

The core construction is the barycentric stochastic interpolant defined for $K+1$ marginals $\{\rho_k\}_{k=0}^K$. The process is parameterized by $\alpha \in \Delta^K$ (the $K$-simplex):

$x(\alpha) = \sum_{k=0}^K \alpha_k x_k,$

with $(x_0, ..., x_K)$ drawn from a coupling that matches each marginal. This generalizes the standard stochastic interpolant for $K=1$, which underlies score-based diffusion and flow-based models.

The framework introduces a set of $K+1$ conditional expectation “vector fields” $g_k(\alpha, x) = E[x_k \mid x(\alpha) = x]$, each minimizing a square loss regression functional, which can be empirically estimated even when the marginal datasets are disjoint. Associated continuity and transport equations over the simplex yield ODE/score-based diffusion processes capable of transporting samples among all marginals.

Path-Independent Decoupling and Transport Cost Optimization

A key technical feature is the decoupling of the path on the simplex (the “schedule” $\alpha(t)$) from the learned conditional vector fields. The generative mapping between two marginals $\rho_i$ and $\rho_j$ is implemented by specifying any path $\alpha(t)$ within the simplex connecting $e_i$ to $e_j$, with the probability flow induced by

$$\dot X_t = \sum_{k=0}^K \dot{\alpha}_k(t) g_k(\alpha(t), X_t).$$

Critically, the path can be itself optimized to minimize a quadratic transport cost—analogous to the Benamou–Brenier action for Wasserstein-2—but without requiring recomputation of the learned vector fields. This insight leads to a practical reduction in integration complexity for flows between marginals.

Figure 1: Direct optimization of $\alpha(t)$ over a parametric class reduces transport cost between a Gaussian and a checkerboard density; learned $\alpha$ outperforms linear interpolation and yields more efficient probability flow.

Applications: All-to-All Image Translation and Emergent Style Transfer

For $K \gg 1$, a single trained model concurrently learns all pairwise correspondences among the marginals via shared vector fields. The multimarginal setting supports direct, flexible all-to-all mapping and allows for translation between an arbitrary pair without the inefficiencies of training $O(K^2)$ separate models.

On image translation tasks (MNIST digits, AFHQ, CelebA, Oxford Flowers), the model is trained to smoothly transfer features among all domains while preserving semantic content. Notably, when the generative models are trained over the entire simplex, rather than individual edges, the resulting transformations exhibit improved content preservation and style blending.

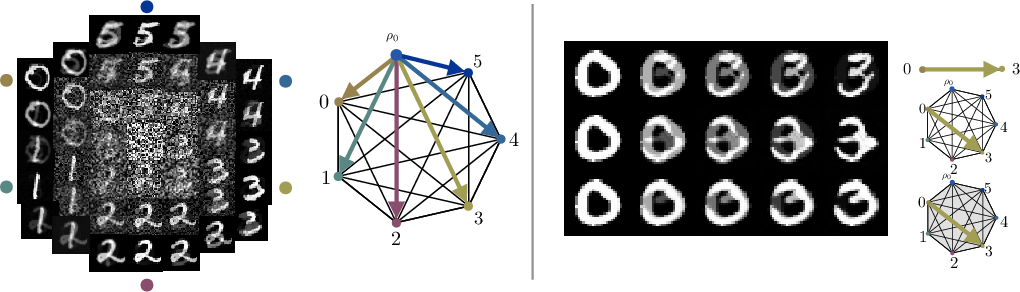
Figure 2: Left—MNIST digits generated from a fixed Gaussian latent, mapped to each of six classes by traversing simplex edges; Right—Translation between classes improves when training occurs over higher-order simplex structures.

The model’s flexibility enables traversing non-edge paths across the simplex, which can result in samples with similar global content yet with subtle semantic or textural variety depending on the path taken.

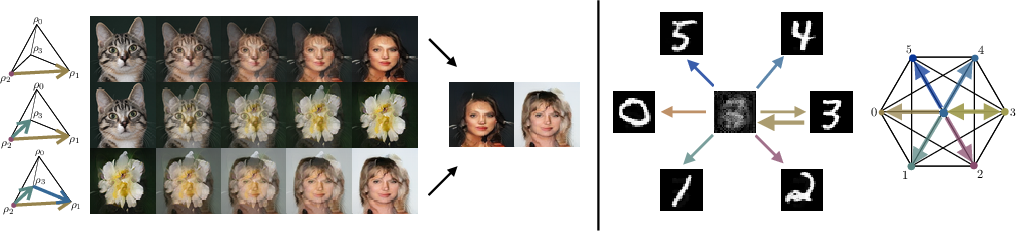
Figure 3: Traversing different paths on the simplex from 'cat' to 'celebrity' (possibly via 'flower') produces target domain samples with preserved semantic structure.

Additionally, multimarginal training naturally enables barycentric generation—transporting samples through the interior of the simplex, yielding outputs with blended characteristics and emergent style transfer.

Figure 4: Left—Sampling endpoints of the simplex among AFHQ, flowers, and CelebA shows diverse mappings. Right—A single interpolant enables emergent style transfer, smoothly mixing semantic and structural features across datasets.

Theoretical Ramifications

The stochastic interpolant-based multimarginal framework extends the structural results of Monge-type and barycentric couplings from the optimal transport literature [Pass 2014, Agueh & Carlier 2011]. The conditional expectations $g_k$ in the Monge-case reduce to deterministic compositions of learned deterministic transport maps, but the stochastic empirical construction accommodates more general joint couplings, which are key in high-dimensional generative modeling.

Unlike conventional multimarginal OT, which is computationally intractable for large $K$ due to exponential scaling of plan supports, the stochastic interpolant approach is tractable and enables joint learning with amortized parameterization. This opens new algorithmic horizons for structured joint generation and multi-way data fusion.

Numerical Results

The paper empirically demonstrates:

• Reduced transport cost for optimized paths: In two-marginal settings, direct optimization over the interpolant path produces quantifiably shorter probability flows, resulting in faster convergence of ODE integration and reduced function evaluations.
• Improved translation in multimarginal settings: For both MNIST and image domain translation, models trained over the full simplex yield superior content preservation compared to edge-wise or pairwise models alone.
• Multi-way semantic preservation: Path traversals across interior simplex points enable controllable, multi-hop transformation, while the learned flows facilitate content transfer and style mixing unattainable with pairwise models.

Implications and Future Directions

The multimarginal stochastic interpolant paradigm provides a unified, extensible approach for learning joint models with arbitrary marginal constraints. Its decoupling of path and field learning aligns closely with geometric optimal transport, yet offers significantly greater practical flexibility and scalability. The implications extend to novel tasks in structured translation, data harmonization, style transfer, and algorithmic fairness, where multi-way correspondences are essential.

Further research could extend this construction to:

• Integration with high-dimensional diffusion models;
• Adaptive learning of more general (potentially non-linear) interpolants for tighter approximations to optimal transport solutions;
• Application to multi-modal generative tasks with constraint-satisfying correspondence structure (e.g., multi-label data, fairness-constrained synthesis);
• Direct extensions to continuous and functional data domains;
• Exploration of how path-dependent multimarginal flows interact with learned latent structure and downstream task performance.

Conclusion

This work establishes a flexible and theoretically principled framework for generative modeling with multimarginal constraints via barycentric stochastic interpolants. The framework enables the efficient and interpretable coupling of $K+1$ arbitrary distributions, supports both joint sample synthesis and style transfer, and provides a practical path for reducing transport costs. Its compositionality and scalability suggest broad applicability in AI and generative modeling, especially in contexts requiring the synthesis or translation across multiple, structured data domains.