Papers
Topics
Authors
Recent
Assistant
AI Research Assistant
Well-researched responses based on relevant abstracts and paper content.
Custom Instructions Pro
Preferences or requirements that you'd like Emergent Mind to consider when generating responses.
Gemini 2.5 Flash
Gemini 2.5 Flash 161 tok/s
Gemini 2.5 Pro 52 tok/s Pro
GPT-5 Medium 32 tok/s Pro
GPT-5 High 33 tok/s Pro
GPT-4o 108 tok/s Pro
Kimi K2 207 tok/s Pro
GPT OSS 120B 471 tok/s Pro
Claude Sonnet 4.5 36 tok/s Pro
2000 character limit reached

Latent Diffusion Models for Structural Component Design (2309.11601v2)

Published 20 Sep 2023 in cs.LG

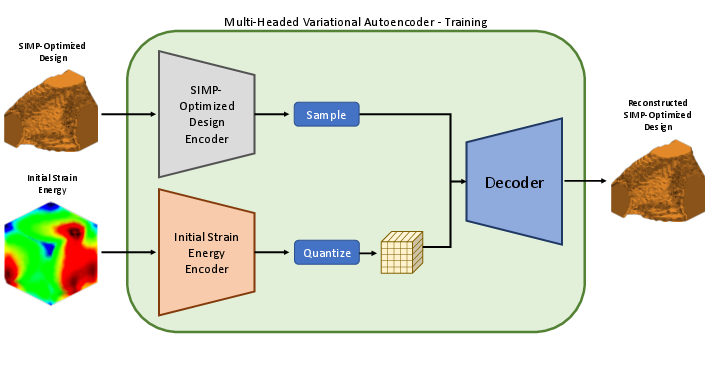
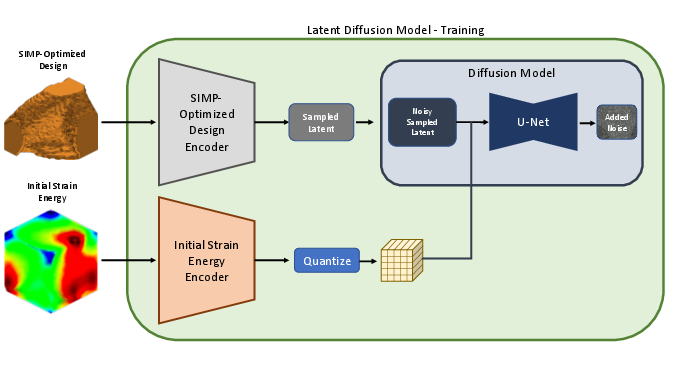
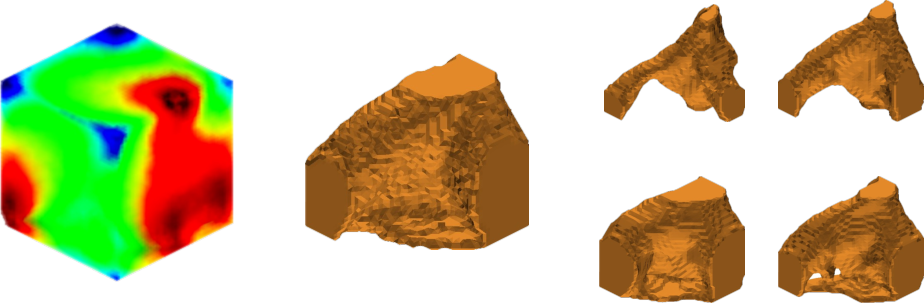
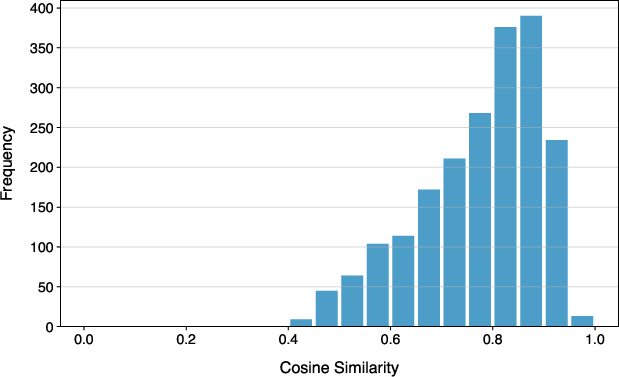
Abstract: Recent advances in generative modeling, namely Diffusion models, have revolutionized generative modeling, enabling high-quality image generation tailored to user needs. This paper proposes a framework for the generative design of structural components. Specifically, we employ a Latent Diffusion model to generate potential designs of a component that can satisfy a set of problem-specific loading conditions. One of the distinct advantages our approach offers over other generative approaches, such as generative adversarial networks (GANs), is that it permits the editing of existing designs. We train our model using a dataset of geometries obtained from structural topology optimization utilizing the SIMP algorithm. Consequently, our framework generates inherently near-optimal designs. Our work presents quantitative results that support the structural performance of the generated designs and the variability in potential candidate designs. Furthermore, we provide evidence of the scalability of our framework by operating over voxel domains with resolutions varying from $323$ to $1283$. Our framework can be used as a starting point for generating novel near-optimal designs similar to topology-optimized designs.

Definition Search Book Streamline Icon: https://streamlinehq.com
References (52)
  1. Generative adversarial networks, 2014.
  2. Image-to-image translation with conditional adversarial networks, 2018.
  3. Scaling up gans for text-to-image synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2023.
  4. Designing for additive manufacturing: lightweighting through topology optimization enables lunar spacecraft. Journal of Mechanical Design, 139(10), 2017.
  5. A survey of manufacturing oriented topology optimization methods. Advances in Engineering Software, 100:161–175, 2016.
  6. Computational acceleration of topology optimization using deep learning. Applied Sciences, 13(1), 2023. ISSN 2076-3417. doi: 10.3390/app13010479.
  7. Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 1988.
  8. Martin P Bendsøe. Optimal shape design as a material distribution problem. Structural optimization, 1(4):193–202, 1989.
  9. A level set method for structural topology optimization. Computer methods in applied mechanics and engineering, 192(1-2):227–246, 2003.
  10. A level-set based topology optimization using the element connectivity parameterization method. Structural and Multidisciplinary Optimization, 42:269–282, 2010.
  11. Genetic Algorithms in Structural Topology Optimization, pages 117–133. Springer Netherlands, Dordrecht, 1993. ISBN 978-94-011-1804-0.
  12. S.Y. Wang and K. Tai. Structural topology design optimization using genetic algorithms with a bit-array representation. Computer Methods in Applied Mechanics and Engineering, 194(36):3749–3770, 2005. ISSN 0045-7825.
  13. Palette: Image-to-image diffusion models, 2022.
  14. On the use of artificial neural networks in topology optimisation. Structural and Multidisciplinary Optimization, 65(10), oct 2022.
  15. Neural networks for topology optimization. Russian Journal of Numerical Analysis and Mathematical Modelling, 34(4):215–223, 2019.
  16. 3D topology optimization using convolutional neural networks. arXiv preprint arXiv:1808.07440, 2018.
  17. Deep learning for determining a near-optimal topological design without any iteration. Structural and Multidisciplinary Optimization, 59(3):787–799, 2019.
  18. A deep convolutional neural network for topology optimization with strong generalization ability. arXiv preprint arXiv:1901.07761, 2019.
  19. Tounn: Topology optimization using neural networks. Structural and Multidisciplinary Optimization (accepted, 2020.
  20. Investigation into the topology optimization for conductive heat transfer based on deep learning approach. International Communications in Heat and Mass Transfer, 97, 2018. ISSN 0735-1933.
  21. Deep learning for topology optimization of 2d metamaterials. Materials & Design, 196:109098, 2020. ISSN 0264-1275.
  22. A novel topology optimization approach using conditional deep learning, 2019.
  23. Deep learning for determining a near-optimal topological design without any iteration. Structural and Multidisciplinary Optimization, 59(3):787–799, Oct 2018. ISSN 1615-1488.
  24. A novel deep learning based method for the computational material design of flexoelectric nanostructures with topology optimization. Finite Elements in Analysis and Design, 165:21–30, 2019. ISSN 0168-874X.
  25. Multi-objective topology optimization of rotating machines using deep learning. IEEE Transactions on Magnetics, 55(6):1–5, 2019. doi: 10.1109/TMAG.2019.2899934.
  26. Accelerated topology optimization by means of deep learning. Structural and Multidisciplinary Optimization, 62, 09 2020.
  27. Algorithmically-consistent deep learning frameworks for structural topology optimization. Engineering Applications of Artificial Intelligence, 106:104483, 2021. ISSN 0952-1976.
  28. Deep generative design: Integration of topology optimization and generative models. Journal of Mechanical Design, 141(11), Sep 2019. ISSN 1528-9001.
  29. Non-iterative structural topology optimization using deep learning. Computer-Aided Design, 115:172–180, 2019. ISSN 0010-4485.
  30. Topology optimization of 2D structures with nonlinearities using deep learning. Computers & Structures, 237:106283, 2020. ISSN 0045-7949.
  31. Topology optimization of ipm motor with aid of deep learning. International Journal of Applied Electromagnetics and Mechanics, 59:1–10, 12 2018.
  32. A deep convolutional neural network for topology optimization with strong generalization ability, 2020.
  33. Design automation by integrating generative adversarial networks and topology optimization. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, volume 51753, page V02AT03A008. American Society of Mechanical Engineers, 2018.
  34. A new data-driven topology optimization framework for structural optimization. Computers & Structures, 239:106310, 2020. ISSN 0045-7949.
  35. An indirect design representation for topology optimization using variational autoencoder and style transfer. In 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, page 0804, 2018.
  36. Cnn-based image recognition for topology optimization. Knowledge-Based Systems, 198:105887, 2020. ISSN 0950-7051.
  37. Topology optimization under uncertainty using a stochastic gradient-based approach, 2019.
  38. Learning-based topology variation in evolutionary level set topology optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, pages 825–832, 2018.
  39. Convolutional neural network-based topology optimization (cnn-to) by estimating sensitivity of compliance from material distribution, 2019.
  40. Accelerating gradient-based topology optimization design with dual-model artificial neural networks. Structural and Multidisciplinary Optimization, pages 1–21, 11 2020.
  41. Generative design by reinforcement learning: Maximizing diversity of topology optimized designs, 2020.
  42. An improved convolutional neural network based on a parameter modification of the convolution layer., 2021.
  43. Optimization of convolutional neural networks using the fuzzy gravitational search algorithm. Journal of Automation, Mobile Robotics and Intelligent Systems, pages 109–120, 2020.
  44. Universal machine learning for topology optimization. Computer Methods in Applied Mechanics and Engineering, 375:112739, 2021. ISSN 0045-7825.
  45. TopologyGAN: Topology Optimization Using Generative Adversarial Networks Based on Physical Fields Over the Initial Domain. Journal of Mechanical Design, 143(3), 02 2021. ISSN 1050-0472.
  46. Topogan topology optimization with generative adversarial networks. Paris, Ecole des Ponts Paristech, 2021.
  47. Diffusion models beat gans on topology optimization, 2022.
  48. Neural discrete representation learning, 2018.
  49. Classifier-free diffusion guidance, 2022.
  50. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017.
  51. Rethinking the inception architecture for computer vision, 2015.
  52. Deep learning-based 3d multigrid topology optimization of manufacturable designs. Engineering Applications of Artificial Intelligence, 126:107033, 2023.
Citations (4)
View on Semantic Scholar

Summary

  • The paper introduces a generative design framework that leverages Latent Diffusion Models and a dual-headed VAE to generate diverse structural component designs.
  • It conditions the latent space using initial strain energy and SIMP-optimized geometries, enabling the generation of multiple design variants from a single input.
  • Performance metrics such as cosine similarity and volume fraction deviations confirm enhanced design uniqueness and structural robustness over traditional methods.

Latent Diffusion Models for Structural Component Design

Introduction

The paper introduces a novel framework for structural component design leveraging Latent Diffusion Models (LDMs). Unlike traditional methods that focus heavily on using procedural modeling and deterministic optimization techniques, this approach utilizes generative modeling to improve design exploration capabilities, particularly in the context of manufacturing and engineering design phases. The choice of LDMs offers notable advantages over GANs and other traditional generative models by mitigating mode collapse and enabling efficient design editing of pre-existing geometries.

Framework Overview

The framework consists of a Multi-Headed Variational Autoencoder (VAE) and a Diffusion Model (DM) operating in the VAE's latent space. The VAE processes the Initial Strain Energy and SIMP-Optimized design geometries to create latent representations. The DM then generates new design variations conditioned on initial conditions, represented as latent codes, effectively allowing the creation of diverse candidate designs from a single input scenario. Figure 1

Figure 1: An overview of training the external Multi-Headed VAE.

Multi-Headed Variational Autoencoder

The external VAE is crucial to the framework, incorporating dual encoder networks—a pathway which encodes Initial Strain Energy into a latent space and another which processes SIMP-Optimized designs. Both pathways contribute to a combined latent representation that the VAE's decoder network subsequently converts back to voxel space, thus reconstructing an approximate SIMP geometry. This dual-headed approach allows integration of conditioning factors into the encoding process directly. Figure 2

Figure 2: An overview of training the Latent Diffusion Model.

Latent Diffusion Model Training

Within the latent space defined by the VAE, the DM iteratively refines candidate design representations. This allows each latent vector to map to various design outcomes depending on the initial random noise input. Figure 3 exemplifies the emergent refinement of initial random Gaussian samples across inference iterations, quantitatively demonstrating improvements in structural features over traditional VAE architectures. Figure 3

Figure 3: Decoded posteriors from the DDPM denoising trajectory during inference. Decoding the initial random Gaussian sample (far left design) highlights the improvement our framework provides over a traditional VAE.

Performance Evaluation

Performance metrics focus on design uniqueness and structural robustness. Figure 4 presents different design variants generated by the model for identical input strain energy conditions, exhibiting variability and suggesting enhanced exploration capability over deterministic methods. Figure 4

Figure 4: Multiple candidate designs for a given Initial Strain Energy Map. From left to right, Initial Strain Energy, SIMP-Optimized Design, and four different generated designs by the proposed framework.

Statistical measures such as cosine similarity and volume fraction deviations provide additional quantitative insight into the generated designs' variability and comparability against SIMP-optimized counterparts (Figures 5 and 6). Figure 5

Figure 5: The distribution of cosine similarity between the SIMP-Optimized design and LDM-Generated designs for a given Initial Strain Energy.

Figure 6

Figure 6: The distributions of volume fractions for SIMP-Optimized designs and LDM-Generated designs.

Discussion and Future Directions

The framework successfully demonstrates the generative capabilities of LDMs in producing multiple plausible structural component designs, thereby broadening the conceptual design phase's scope. Moreover, the potential to operate effectively over 3D voxel domains emphasizes scalability. Future research may explore more advanced conditioning methods, such as user-defined constraints directly influencing volume or structural parameters, enhancing the flexibility and applicability of generative design processes in engineering contexts.

Conclusion

This framework marks a significant advancement in application-specific generative design, emphasizing LDMs' robustness in the design ideation phase. It offers a computationally viable approach to generating near-optimal and diverse design solutions, setting the stage for future exploration and refinement in AI-driven design methodologies.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up