Variations and Relaxations of Normalizing Flows (2309.04433v1)

Abstract: Normalizing Flows (NFs) describe a class of models that express a complex target distribution as the composition of a series of bijective transformations over a simpler base distribution. By limiting the space of candidate transformations to diffeomorphisms, NFs enjoy efficient, exact sampling and density evaluation, enabling NFs to flexibly behave as both discriminative and generative models. Their restriction to diffeomorphisms, however, enforces that input, output and all intermediary spaces share the same dimension, limiting their ability to effectively represent target distributions with complex topologies. Additionally, in cases where the prior and target distributions are not homeomorphic, Normalizing Flows can leak mass outside of the support of the target. This survey covers a selection of recent works that combine aspects of other generative model classes, such as VAEs and score-based diffusion, and in doing so loosen the strict bijectivity constraints of NFs to achieve a balance of expressivity, training speed, sample efficiency and likelihood tractability.

• The paper introduces methodological innovations including SurVAE, Stochastic, and Diffusion Normalizing Flows to relax strict bijective constraints.
• It integrates insights from VAEs and diffusion models to overcome topological and dimensional mismatches inherent in traditional normalizing flows.
• Empirical findings suggest that adding stochastic elements improves training speed and sampling efficiency while enhancing model expressivity.

Variations and Relaxations of Normalizing Flows

Introduction

This paper investigates the structural limitations inherent to Normalizing Flows (NFs) and proposes solutions through integration with other generative model families such as VAEs and diffusion models. NFs, rooted in bijective transformation, express intricate probability distributions but are constrained due to identical input-output dimensionality requirements. Recognizing this challenge, researchers have aimed to relax these constraints, thus enhancing the expressivity while retaining the precise density estimation potential unique to NFs.

Normalizing Flows

Normalizing Flows are elaborated as models that transform a simple distribution into a complex one through a series of diffeomorphic functions, ensuring invertibility and differentiability. The essence of NFs lies in their ability to tightly couple generation and precise likelihood evaluation. These transformations, which are compositions of bijective maps, offer exact sampling capabilities and efficient density calculations via Jacobi determinant manipulations.

However, this paper illustrates that such bijection imposes topological rigidity. Specifically, when the target distribution and base distribution possess disparate support topologies, such as differing numbers of connected components, NFs fail to approximate the target accurately without substantial complexity increases (Figure 1).

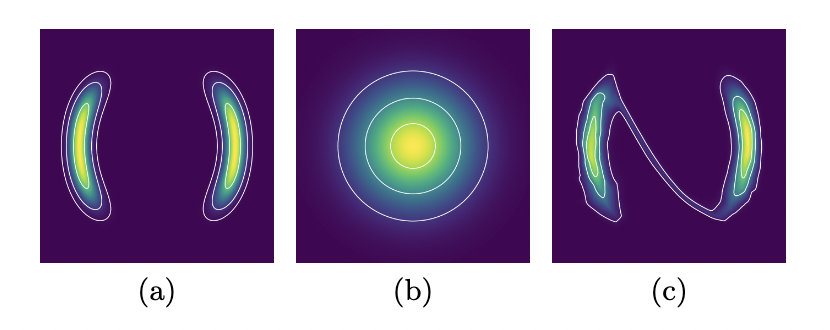
Figure 1: An example of "smearing" in (c), where the target distribution (a) and the base distribution (b) differ in their number of connected components.

Variational Autoencoders

VAEs serve as a contrasting generative model class where expressivity is enhanced through latent variable frameworks. Despite VAEs' ease of training and robustness in complex scenarios, they notoriously suffer from posterior collapse, which undermines the use of latent codes. VAEs optimize the evidence lower bound (ELBO), a practical but often approximate likelihood measure, utilizing the reparameterization trick to maintain computational efficiency during training.

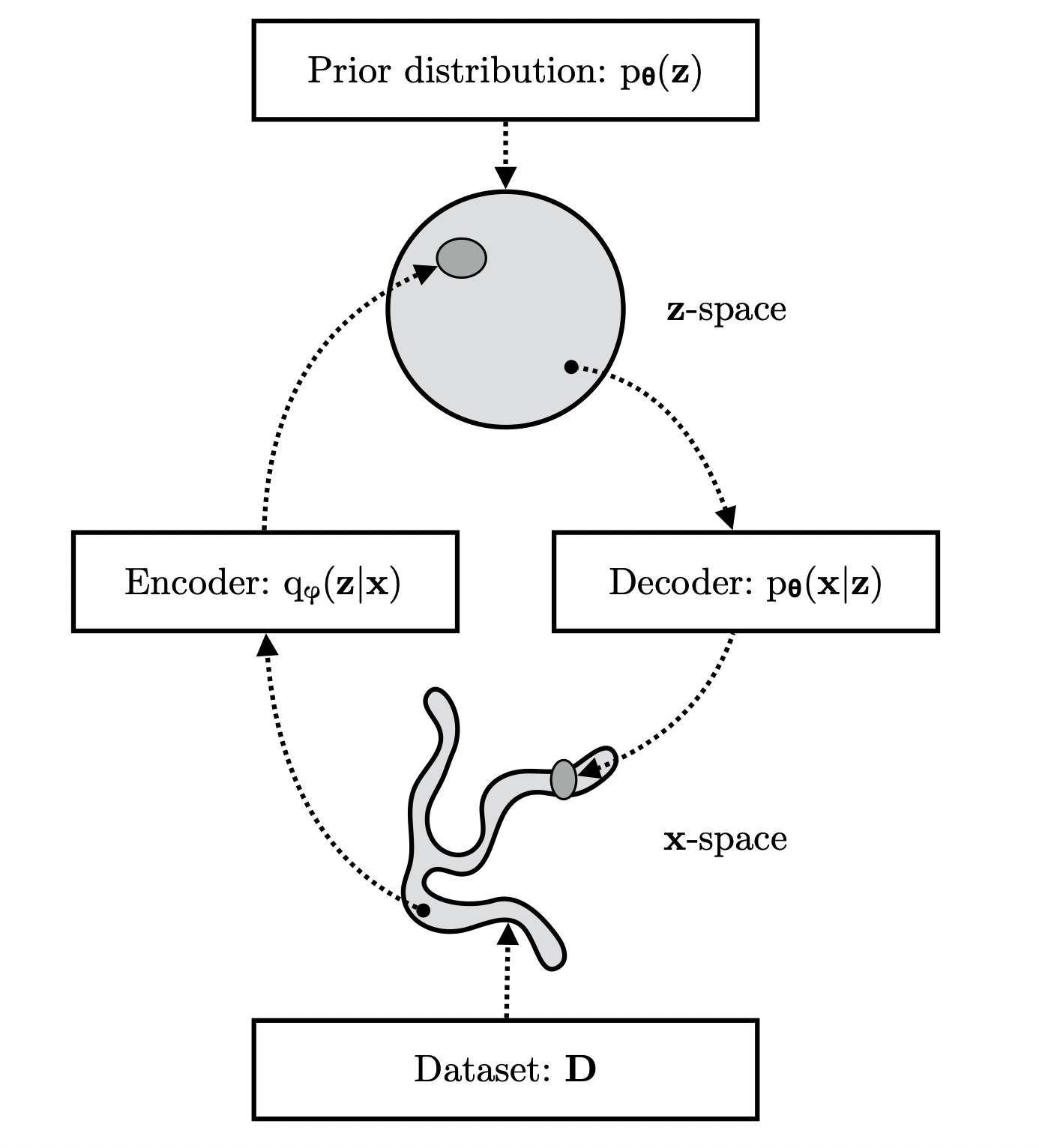
Figure 2: Computational flow in a VAE

.

Denoising Diffusion

Diffusion models, known for iterative latent variable sampling through Markov chains, surpass previous generative models in quality and stability. The paper elucidates the forward diffusion process where data undergoes incremental noisification—a process later reversed through learned conditional distributions. Critically, while denoising score matching elevates output fidelity, the requirement for latent space dimension equality remains a key limitation needing addressal.

Relaxing Constraints

SurVAE Flows

SurVAE Flows provide an interpretative bridge between VAEs and NFs through surjective transformation inclusions, allowing stochastic components while preserving likeliness tractability. The formulation of inference surjections and generative surjections circumvent dimensional tightness, propelling better distribution modeling and sharper boundary representation in complex distributions.

Stochastic Normalizing Flows

Stochastic Normalizing Flows introduce randomness within the NF framework via stochastic blocks, such as Langevin layers, relieving expressive constraints. This inclusion manifests superior capabilities over vanilla Normalizing Flows regarding handling multi-modal distributions and circumventing smearing, exemplified in the double-well scenario (Figure 3).

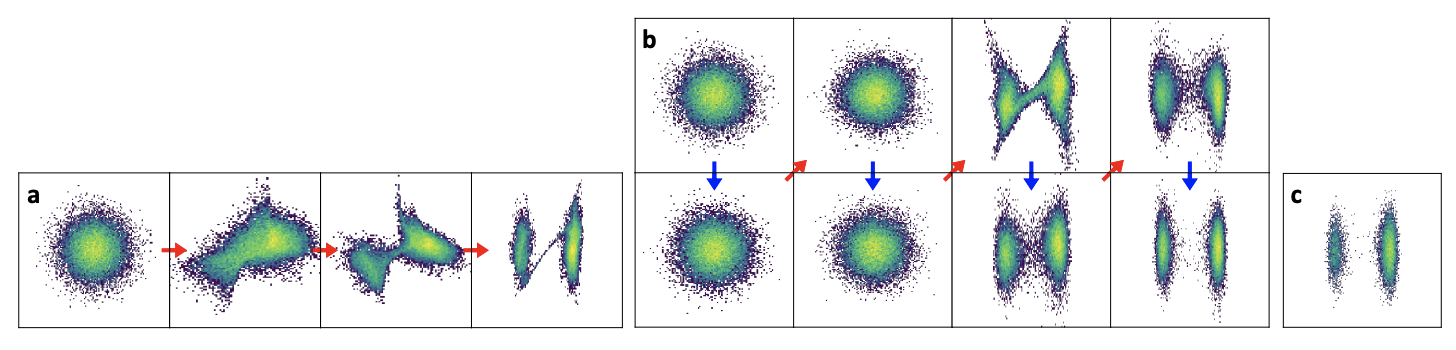
Figure 3: Double well problem: a) Normalizing flows, b) NF with stochasticity, c) Sample from true distribution.

Diffusion Normalizing Flow

DiffFlow amalgamates Normalizing Flows and Diffusion models by embedding noise into the forward pass, trained through mutual KL divergence minimization. Leveraging stochastic differential equations (SDEs), DiffFlow exploits tailored noise application to navigate dimensional and topological limitations, achieving higher expressivity and competitive sampling efficiency.

Discussion

Expressivity: The paper argues that introducing stochasticity into NFs enhances the model's ability to capture complex topologies. VAEs inherently possess higher expressive power through latent space manipulation, though diffusion strategies bolster expressivity by elevating sample fidelity.

Training Speed: Normalizing flows, varied through stochastic layers, alleviate some complexity-imposed inefficiencies, providing faster convergence rates. While score-based models offer robust expressivity, they entail significantly complex training due to the detailed learning process in low-density regions.

Likelihood Computation: Without strict bijective adherence, Stochastic and Diffusion Normalizing Flows compromise exact likelihood computation capabilities. VAEs and score-based models bypass these constraints for approximated likelihood results.

Sampling Efficiency: Despite stochastic enhancements, Normalizing and Diffusion Normalizing Flows diverge on sampling efficiency. While NFs can produce quick samples via deterministic paths, Diffusion Normalizing Flows lag due to their intricate generation processes.

Conclusion

The paper's comparative analysis underscores the tension between expressivity and tractability within generative modeling. By strategically loosening bijective constraints, incorporating stochasticity, and assimilating cross-model advantages, these innovations strive toward more flexible, capable generative frameworks. While direct likelihood computation remains a hurdle, the systems explored hold promise for further developments in efficient generative modeling methodologies.