Generating with Confidence: Uncertainty Quantification for Black-box Large Language Models (2305.19187v3)

Abstract: LLMs specializing in natural language generation (NLG) have recently started exhibiting promising capabilities across a variety of domains. However, gauging the trustworthiness of responses generated by LLMs remains an open challenge, with limited research on uncertainty quantification (UQ) for NLG. Furthermore, existing literature typically assumes white-box access to LLMs, which is becoming unrealistic either due to the closed-source nature of the latest LLMs or computational constraints. In this work, we investigate UQ in NLG for black-box LLMs. We first differentiate uncertainty vs confidence: the former refers to the ``dispersion'' of the potential predictions for a fixed input, and the latter refers to the confidence on a particular prediction/generation. We then propose and compare several confidence/uncertainty measures, applying them to selective NLG where unreliable results could either be ignored or yielded for further assessment. Experiments were carried out with several popular LLMs on question-answering datasets (for evaluation purposes). Results reveal that a simple measure for the semantic dispersion can be a reliable predictor of the quality of LLM responses, providing valuable insights for practitioners on uncertainty management when adopting LLMs. The code to replicate our experiments is available at https://github.com/zlin7/UQ-NLG.

• The paper pioneers uncertainty quantification for black-box large language models using response similarity and spectral graph analysis.
• It employs novel measures such as Jaccard similarity, NLI-based entailment, and eigenvalue analysis to assess response consistency and semantic diversity.
• Empirical results show improved AUROC and AUARC metrics on QA datasets, demonstrating enhanced reliability in LLM output generation.

Uncertainty Quantification for Black-box LLMs

The paper "Generating with Confidence: Uncertainty Quantification for Black-box LLMs" investigates the challenge of uncertainty quantification (UQ) in natural language generation (NLG) using black-box access to LLMs. The focus is on evaluating the reliability of LLM-generated responses by developing uncertainty and confidence measures that do not require white-box access.

Introduction

LLMs have shown impressive capabilities in NLG tasks, yet assessing the trustworthiness of their outputs remains challenging. Previous approaches to UQ in machine learning often assume white-box access to models, which is not always feasible with the latest closed-source LLMs. This paper addresses the need for UQ strategies that can operate with black-box LLMs, providing techniques to estimate both uncertainty and confidence in LLM outputs.

Background and Definitions

The paper differentiates between uncertainty and confidence: uncertainty refers to the dispersion of potential predictions for an input, evaluated globally for a dataset, whereas confidence measures the trust in a specific prediction. In NLG, predictive uncertainty and confidence must account for the high-dimensional and potentially semantically equivalent outputs that LLMs produce. This complexity necessitates innovative approaches for accurate UQ in NLG tasks.

Proposed Methods

The paper introduces several mechanisms for quantifying uncertainty and confidence using black-box strategies:

• Response Similarity: The paper employs measures like Jaccard similarity and Natural Language Inference (NLI) to evaluate the semantic equivalence of generated responses. NLI classifiers help determine entailment or contradiction between responses.
• Uncertainty Measures: Techniques like the number of semantic sets and the sum of eigenvalues of the graph Laplacian are proposed to estimate input uncertainty by analyzing response dispersion.
• Confidence Measures: Methods using the degree matrix and eccentricity in a response embedding space offer confidence scores, indicating the consistency of a response relative to others.

Experiments and Evaluation

The paper evaluates the proposed UQ methods on QA datasets (e.g., TriviaQA, Natural Questions) using various LLMs (LLaMA, OPT, GPT-3.5-turbo). The key evaluation metrics include the Area Under Receiver Operating Characteristic (AUROC) and Area Under Accuracy-Rejection Curve (AUARC), which assess the ability of UQ measures to predict the correctness of LLM outputs.

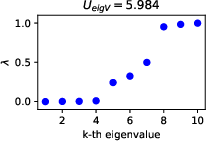
Figure 1: The distribution of the eigenvalues of the graph Laplacian generated by $NLI_{entail}$, showing the semantic diversity in responses and its correlation with uncertainty.

Results

The paper finds that the proposed UQ mechanisms, particularly response similarity-based methods using NLI, outperform traditional white-box UQ methods. The semantic measures effectively identify uncertain inputs and confidently rank specific LLM responses. Notably, AUARCs imply substantial improvements in response accuracy when leveraging these UQ methods for selective generation.

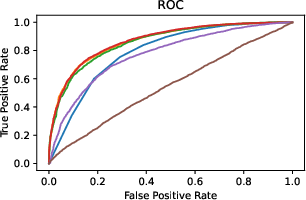
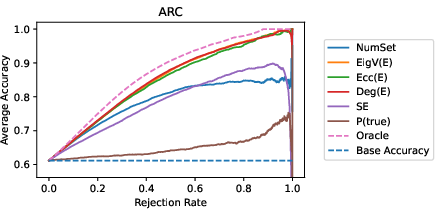
Figure 2: ROC and ARC comparisons illustrating the improved predictive capability of uncertainty measures in black-box settings.

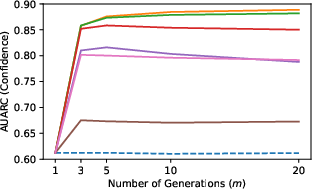
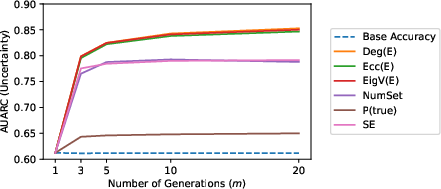
Figure 3: AUARC improvement with varying numbers of sampled responses, highlighting the scalability of the proposed methods.

Conclusion

The research provides a framework for robust uncertainty quantification in black-box LLMs, crucial for enhancing the reliability of NLG applications. It addresses the limitations of previous white-box-centric methodologies and lays the groundwork for future exploration into UQ without model internals. Further research could refine these methods for more open-ended generation tasks and investigate broader applications across different LLM architectures.