Faith and Fate: Limits of Transformers on Compositionality (2305.18654v3)

Abstract: Transformer LLMs have sparked admiration for their exceptional performance on tasks that demand intricate multi-step reasoning. Yet, these models simultaneously show failures on surprisingly trivial problems. This begs the question: Are these errors incidental, or do they signal more substantial limitations? In an attempt to demystify transformer LLMs, we investigate the limits of these models across three representative compositional tasks -- multi-digit multiplication, logic grid puzzles, and a classic dynamic programming problem. These tasks require breaking problems down into sub-steps and synthesizing these steps into a precise answer. We formulate compositional tasks as computation graphs to systematically quantify the level of complexity, and break down reasoning steps into intermediate sub-procedures. Our empirical findings suggest that transformer LLMs solve compositional tasks by reducing multi-step compositional reasoning into linearized subgraph matching, without necessarily developing systematic problem-solving skills. To round off our empirical study, we provide theoretical arguments on abstract multi-step reasoning problems that highlight how autoregressive generations' performance can rapidly decay with\,increased\,task\,complexity.

• The paper demonstrates that transformer models suffer from error propagation and shallow pattern recognition when tackling complex, multi-hop compositional tasks.
• It introduces a computational graph framework to quantify task complexity in terms of reasoning depth and width, linking higher complexity to lower accuracy.
• Results show that although finetuning improves in-domain performance, models still struggle with out-of-domain examples, calling for new strategies in systematic reasoning.

Faith and Fate: Limits of Transformers on Compositionality

Introduction

Transformers, particularly LLMs like GPT-3, ChatGPT, and GPT-4, have demonstrated remarkable capabilities in various cognitive tasks, yet they face challenges with seemingly simple tasks. This paper investigates such limitations by exploring three representative compositional tasks—multi-digit multiplication, logic grid puzzles, and a dynamic programming problem—to quantify task complexity and model performance systematically.

Compositional Graph Framework

To systematically analyze the reasoning abilities of transformer models, the paper proposes depicting tasks as computation graphs. Each graph's nodes represent variables during execution, while the edges signify function arguments involved in computations (Figure 1). This framework allows measuring compositional complexity in terms of reasoning depth and width, where reasoning depth equates to the maximum multi-hop reasoning required, and reasoning width relates to the degree of parallelism needed during computation.

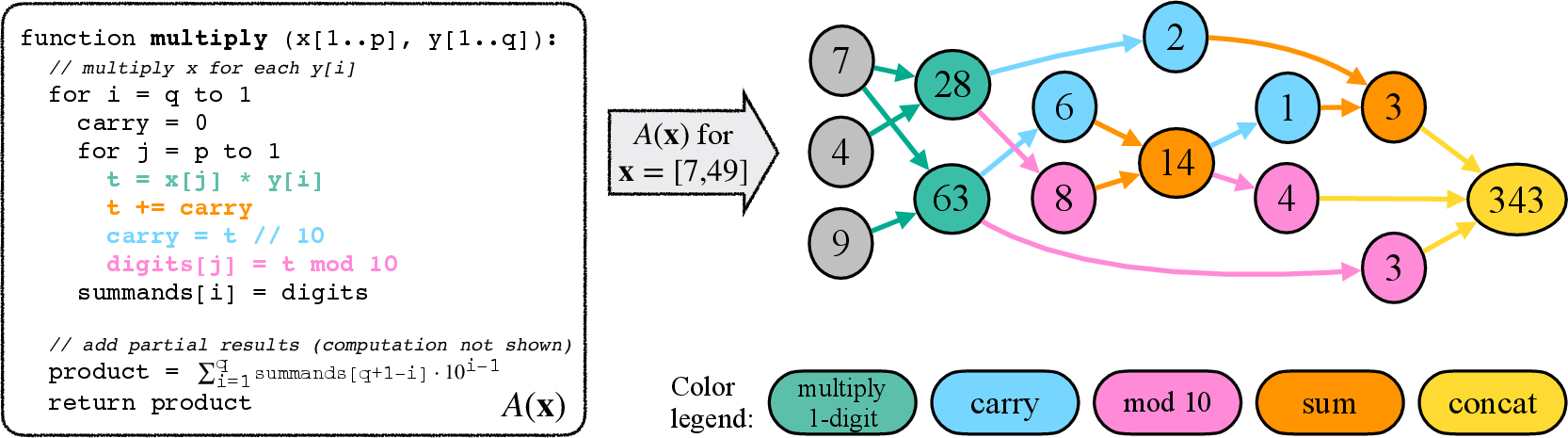
Figure 1: Transformation of an algorithm A to its computational graph $G_{A(\mathbf{x})}$. The depicted example is of long-form multiplication algorithm $A$, for inputs $\mathbf{x} = [7, 49]$ (computing $7 \times 49$).

Empirical Evaluation

The paper conducts comprehensive zero-shot, few-shot, and finetuning experiments with various LLMs to evaluate their performance on compositional tasks. Results show a significant performance drop as task complexity increases, regardless of whether models use question-answer or question-scratchpad formats.

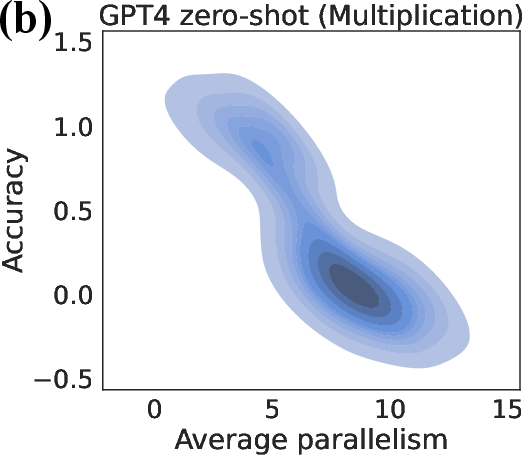
Figure 2: (a) Zero-shot accuracy deteriorates as task complexity increases based on problem sizes. (b) Average parallelism negatively correlates with accuracy.

Despite finetuning with comprehensive data, models achieve high accuracy only on in-domain data while failing to generalize to out-of-domain (OOD) examples. Attempts to introduce explicit scratchpads, intended to guide models through the reasoning path, similarly failed to address the underlying limitations.

Error Analysis and Understanding of Limitations

The paper conducts a detailed error analysis to uncover how transformers handle compositional reasoning. Transformers are found to often fail due to propagation errors, as they lack the capacity to efficiently compose correct reasoning paths.

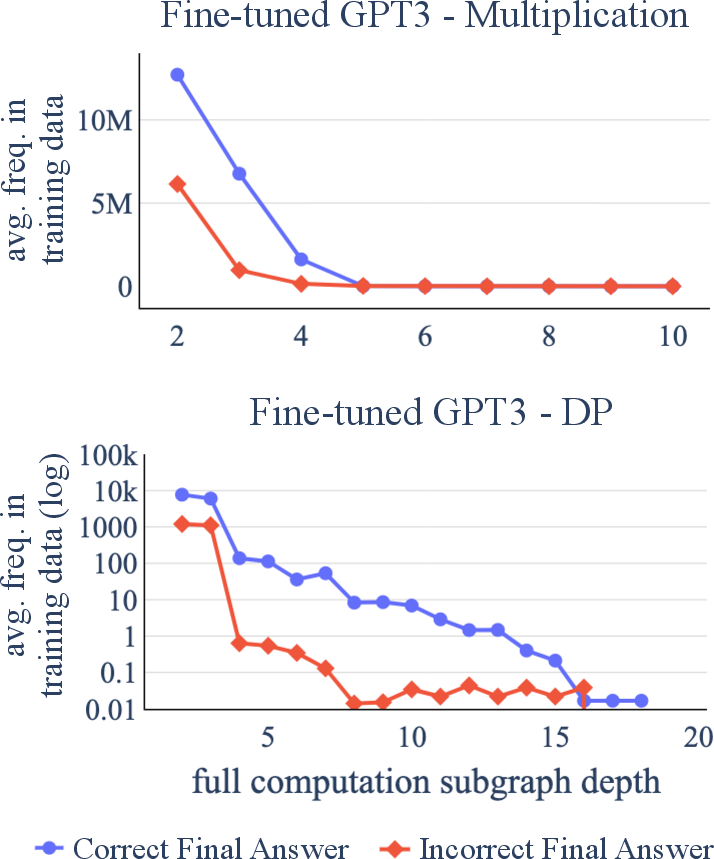
Figure 3: Average frequency in which test examples' full computations subgraph appear in the training data w.r.t. the subgraph depth, grouped by final answer.

The models' tendency towards shallow pattern recognition rather than genuine understanding underlines a fundamental restriction in their current architecture when tackling compositionally complex tasks.

Theoretical Insights

The paper puts forth theoretical propositions that highlight the convergence of error probabilities in transformers when tasked with complex compositional problems. In particular, error rates increase rapidly when either independent applications or iterative applications of functions are required. These findings confirm that transformers may inherently struggle with out-of-box compositionally complex task solutions.

Future Directions

Achieving significant improvements in transformers requires addressing fundamental limitations. Strategies such as leveraging transformers in less complex compositional tasks, integrating planning modules and refining methods, and involving the broader research community are proposed as potential pathways forward. These approaches focus on mitigating error propagation and enhancing systematic reasoning capabilities.

Conclusion

This paper offers critical insights into the limitations of transformers in solving compositionally rich tasks. By highlighting these shortcomings both empirically and theoretically, it underscores the importance of developing more advanced models capable of genuine multi-step reasoning and systematic problem-solving. Understanding these limitations paves the way for future research aimed at creating more reliable AI systems.