Kernel Density Matrices for Probabilistic Deep Learning (2305.18204v3)

Abstract: This paper introduces a novel approach to probabilistic deep learning, kernel density matrices, which provide a simpler yet effective mechanism for representing joint probability distributions of both continuous and discrete random variables. In quantum mechanics, a density matrix is the most general way to describe the state of a quantum system. This work extends the concept of density matrices by allowing them to be defined in a reproducing kernel Hilbert space. This abstraction allows the construction of differentiable models for density estimation, inference, and sampling, and enables their integration into end-to-end deep neural models. In doing so, we provide a versatile representation of marginal and joint probability distributions that allows us to develop a differentiable, compositional, and reversible inference procedure that covers a wide range of machine learning tasks, including density estimation, discriminative learning, and generative modeling. The broad applicability of the framework is illustrated by two examples: an image classification model that can be naturally transformed into a conditional generative model, and a model for learning with label proportions that demonstrates the framework's ability to deal with uncertainty in the training samples. The framework is implemented as a library and is available at: https://github.com/fagonzalezo/kdm.

• The paper presents Kernel Density Matrices (KDMs) that extend traditional density matrices to RKHS for unified modeling of discrete and continuous probabilities.
• It employs both non-parametric and parametric approaches to enable accurate density estimation and probabilistic inference within deep models.
• Experiments show competitive performance in bidirectional classification, conditional generation, and handling label proportions under weak supervision.

Kernel Density Matrices for Probabilistic Deep Learning

The paper "Kernel Density Matrices for Probabilistic Deep Learning" introduces Kernel Density Matrices (KDMs) as a novel mechanism to represent joint probability distributions of continuous and discrete random variables. By extending the concept of density matrices from quantum mechanics into a reproducible kernel Hilbert space (RKHS), the authors provide a differentiable framework for density estimation, inference, and sampling, integrated naturally with deep neural models.

Introduction to Kernel Density Matrices (KDM)

Conceptual Framework

The notion of density matrices from quantum mechanics is pivotal in representing quantum states, incorporating both classical and quantum uncertainties. Density matrices are Hermitian, positive-semidefinite, and act within the Hilbert space representing the quantum system's state space. This research extends density matrices to RKHS, creating Kernel Density Matrices (KDMs) to unify discrete and continuous probability distributions for applications in machine learning.

Density Matrices

A density matrix $\rho$ can be expressed as:

$\rho = \sum_i^N p_i|\psi_i\rangle\langle\psi_i|$

where $p_i$ are probabilities associated with states $|\psi_i\rangle$. Extending this to RKHS permits application to various machine learning tasks.

Implementation of KDMs

Discrete and Continuous KDMs

Discrete KDMs utilize kernels like the cosine kernel, suitable for finite dimension RKHS, to represent categorical distributions. Continuous KDMs employ radial basis kernels such as the Gaussian kernel, fulfilling necessary conditions for density representation.

Probabilistic Training

Non-Parametric Density Estimation

Based on Kernel Density Estimation (KDE), non-parametric density estimation using KDMs ensures convergence in probability for continuous probability distributions.

Parametric Density Estimation

Parametric estimation involves maximizing likelihoods, representing a flexible approach to adapt the kernel parameters for training data.

Joint Densities and Inference

Inference using KDMs revolves around transforming input distributions to output distributions, maintaining expressiveness, compositionality, and reversibility—mimicking quantum measurement operations applied in classical machine learning contexts.

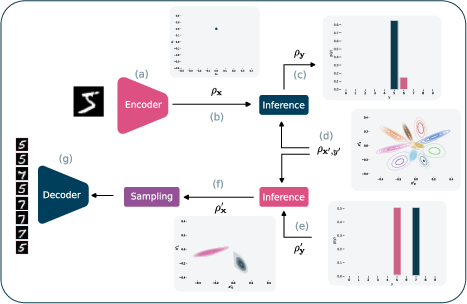
Figure 1: Classification and generation with KDMs. The encoder maps input samples into a latent space, projected as a KDM, facilitating inference with model parameters.

Experiments

Bidirectional Classification and Conditional Generation

Figure 1 illustrates a classifier enhanced by KDM inference modules, transitioning seamlessly between classification and conditional generation. KDM models show performance on par with conventional deep learning models, with added versatility in data generation.

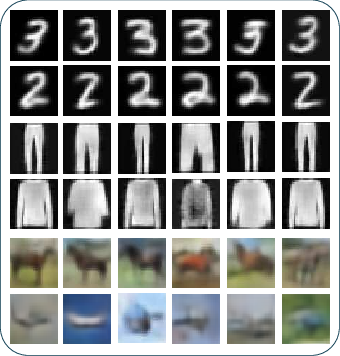
Figure 2: Conditional image generation from Mnist, Fashion-Mnist, and Cifar-10 using the KDM conditional generative model, each row corresponds to a different class.

Learning with Label Proportions

The second experiment showcases KDMs in handling label proportions, demonstrating its adaptability to weakly supervised learning scenarios. KDM's probabilistic modeling of bag uncertainties achieves competitive performance compared to state-of-the-art LLP algorithms.

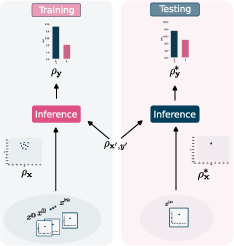
Figure 3: KDM model for classification with label proportions. Model receives bags of instances during training, representing uncertainty effectively.

Conclusion

The paper introduces Kernel Density Matrices as a robust framework for probabilistic deep learning, capable of integrating density matrices into machine learning models efficiently. This contributes significantly to both theoretical and practical aspects of AI, offering new pathways in quantum machine learning applications and inviting future exploration in KDM-centric methodologies.

The versatility of KDMs in various AI applications—spanning from data inference to conditional generation—highlights the potential for further research into broader machine learning contexts and tools leveraging quantum-inspired principles.