A Closer Look at In-Context Learning under Distribution Shifts (2305.16704v1)

Abstract: In-context learning, a capability that enables a model to learn from input examples on the fly without necessitating weight updates, is a defining characteristic of LLMs. In this work, we follow the setting proposed in (Garg et al., 2022) to better understand the generality and limitations of in-context learning from the lens of the simple yet fundamental task of linear regression. The key question we aim to address is: Are transformers more adept than some natural and simpler architectures at performing in-context learning under varying distribution shifts? To compare transformers, we propose to use a simple architecture based on set-based Multi-Layer Perceptrons (MLPs). We find that both transformers and set-based MLPs exhibit in-context learning under in-distribution evaluations, but transformers more closely emulate the performance of ordinary least squares (OLS). Transformers also display better resilience to mild distribution shifts, where set-based MLPs falter. However, under severe distribution shifts, both models' in-context learning abilities diminish.

• The paper demonstrates that transformers can closely emulate OLS regression compared to set-based MLPs in in-context learning settings.
• The study employs linear regression experiments under controlled mild and severe distribution shifts to assess model resilience.
• Both architectures show significant limitations under severe shifts, highlighting the need for refined ICL approaches in LLMs.

A Closer Look at In-Context Learning under Distribution Shifts

This paper presents a focused examination of in-context learning (ICL) within the framework of distribution shifts, using the specific task of linear regression to explore the performance of different architectural models. The analysis juxtaposes transformers, widely prevalent in LLMs, with simpler architectures like set-based Multi-Layer Perceptrons (MLPs) to delineate their abilities and limitations under varying distribution shifts.

Introduction to In-Context Learning

In-context learning (ICL) is an intrinsic feature of LLMs, such as GPT-3 and GPT-4, allowing them to leverage input examples during test time without necessitating any update in model weights. However, understanding the sources and limits of such capabilities remains a developing area of research. The question at the heart of this paper is to determine the extent to which traditional architectures, particularly transformers, can perform ICL when subjected to varying distribution shifts in tasks as fundamental as linear regression.

The research aims to compare transformers to models built using set-based MLPs, which might be perceived as well-aligned with the permutation-invariant nature of the input data for ICL. The core inquiry revolves around the capability of transformers versus simpler models in sustaining ICL, especially when facing out-of-distribution scenarios.

Methodology

Theoretical Foundation

The authors describe the learning task using a standard linear regression model where the inputs $x \in \mathbb{R}^{d}$ and labels $y \in \mathbb{R}$, with input-label pairs forming sequences or 'prompts'. The key focus is on determining under which conditions a model can effectively perform the ordinary least squares (OLS) or ridge regression under various distribution shifts and without parameter updates. The paper derives conditions for optimal model behavior, showing that transformers are more resilient to distribution shifts compared to MLP-based architectures, although both architectures struggled under severe distribution shifts.

Experimental Setup

The experiments aim to elucidate the ability of transformers and MLP-based models to emulate the ordinary least squares algorithm under in-distribution (ID-ICL) and out-of-distribution in-context learning (OOD-ICL). The paper considers two types of distribution shifts: mild and severe. It contemplates changes in the mean of the test prompt inputs, assessing the models' performances in noiseless and noisy scenarios.

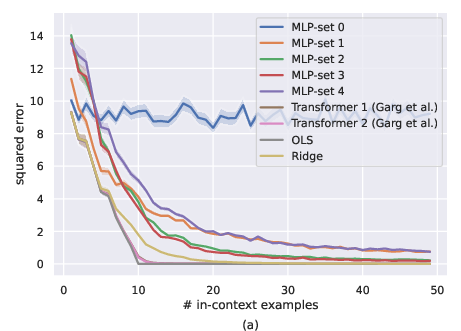
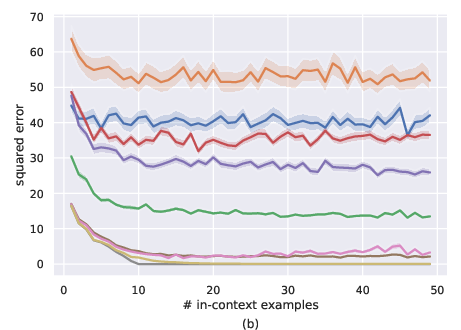
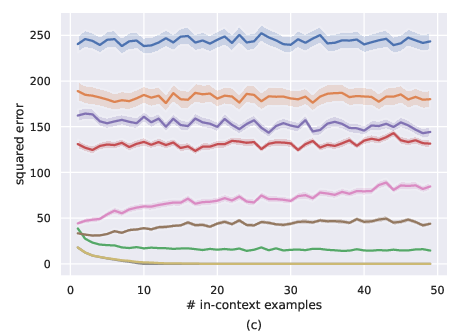
Figure 1: Comparison of MLP-set and transformers for noiseless setting, i.e., $\sigma=0$. a) ID-ICL ($\mu=0$), b) OOD-ICL (Mild distribution shift with $\mu = 2 \cdot \boldsymbol{1})$.

The experiments involve using data generated based on a specified linear function with inputs sampled from a normal distribution, both in training and testing. To comprehension the intensities of distribution shifts, the test prompts are centered differently: mild shift occurs at $\mu = 2 \cdot \boldsymbol{1}$, while severe distribution shift is represented by $\mu = 4 \cdot \boldsymbol{1}$.

Results

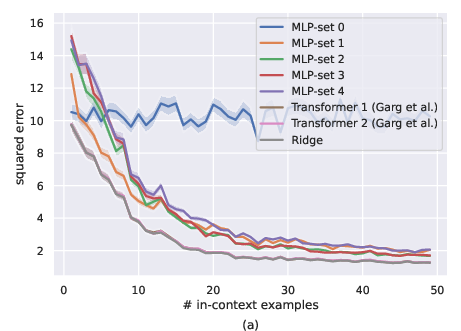
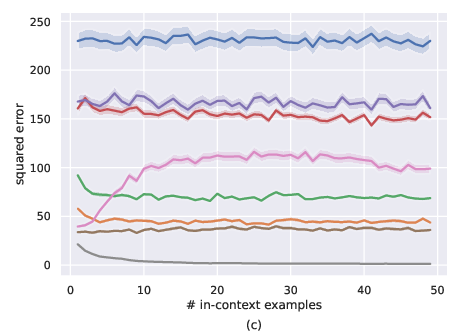
Figure 2: Comparison of MLP-set and transformers for noiseless setting, i.e., $\sigma=0$. a) ID-ICL (µ=0), b) OOD-ICL (Mild distribution shift with $\mu = 2 \cdot \boldsymbol{1$), c) Severe distribution shift with $\mu = 4 \cdot \boldsymbol{1})

.

Figure 1: Comparison of MLP-set and transformers for endotemporal learning (ETL) with σ = 0.

Transformers, particularly the GPT-2-based Transformer 1 and Transformer 2, consistently outperformed the set-based MLPs in in-distribution ICL (ID-ICL) settings, achieving closer results to the OLS model, as seen in Figure 1a and Figure 2a in both the noiseless and noisy environments. Under mild distribution shifts, transformers depicted more stable performance degradation compared to MLPs, which demonstrated more erratic behaviors. However, both architectures were found inadequate under severe distribution shifts, indicating a significant drop in their ICL capabilities.

Conclusion

Through an in-depth theoretical and experimental exploration, the analysis establishes that transformers exhibit superior performance over set-based MLPs in maintaining in-context learning abilities under mild distribution shifts, particularly demonstrated in their ability to emulate OLS regression more effectively. Although both models faltered under severe distribution shifts, transformers showed a more gradual decline.

Future endeavors should focus on dissecting the factors contributing to the superior ICL performance of transformers, potentially considering variations in model architecture, optimization processes, and other inductive biases. Exploring these components could yield significant insights into the generalization abilities of these models under different algorithmic scopes and distributional shifts. Understanding such dimensions holds the potential to enhance future LLMs' capacity to effectively and safely handle a broader range of real-world applications and emergent tasks.