Residual Dynamics Learning for Trajectory Tracking for Multi-rotor Aerial Vehicles (2305.15791v2)

Abstract: This paper presents a technique to cope with the gap between high-level planning, e.g., reference trajectory tracking, and low-level controlling using a learning-based method in the plan-based control paradigm. The technique improves the smoothness of maneuvering through cluttered environments, especially targeting low-speed velocity profiles. In such a profile, external aerodynamic effects that are applied on the quadrotor can be neglected. Hence, we used a simplified motion model to represent the motion of the quadrotor when formulating the Nonlinear Model Predictive Control (NMPC)-based local planner. However, the simplified motion model causes residual dynamics between the high-level planner and the low-level controller. The Sparse Gaussian Process Regression-based technique is proposed to reduce these residual dynamics. The proposed technique is compared with Data-Driven MPC. The comparison results yield that an augmented residual dynamics model-based planner helps to reduce the nominal model error by a factor of 2 on average. Further, we compared the proposed complete framework with four other approaches. The proposed approach outperformed the others in terms of tracking the reference trajectory without colliding with obstacles with less flight time without losing computational efficiency.

• The paper presents a novel approach integrating Sparse Gaussian Process regression with MPC to mitigate residual dynamics for improved UAV trajectory tracking.
• The paper employs a computationally efficient technique by reducing GP complexity from O(n^3) to O(nm^3) using inducing points to capture essential dynamics.
• The paper demonstrates its method through simulations and real-world tests, significantly reducing RMSE and enhancing UAV navigation in cluttered environments.

"Residual Dynamics Learning for Trajectory Tracking for Multi-rotor Aerial Vehicles"

Introduction

The paper introduces a technique to model the residual dynamics between a high-level planner and a low-level controller for multi-rotor aerial vehicles. The research emphasizes minimizing residual dynamics that arise due to kinematical modeling, which is a common scenario in cluttered environments where aggressive maneuvers are constrained. The authors propose using a Sparse Gaussian Process Regression-based technique to model these residual dynamics, which can lead to improved trajectory tracking without the need for complex dynamic models.

Framework and Methodology

The framework is based on enhancing Model Predictive Control (MPC) by learning the residual dynamics using a Sparse Gaussian Process (SGP). The key challenge addressed is the discrepancy between the high-level control generated by MPC and the low-level control executed by the flight controller, which cannot be estimated analytically.

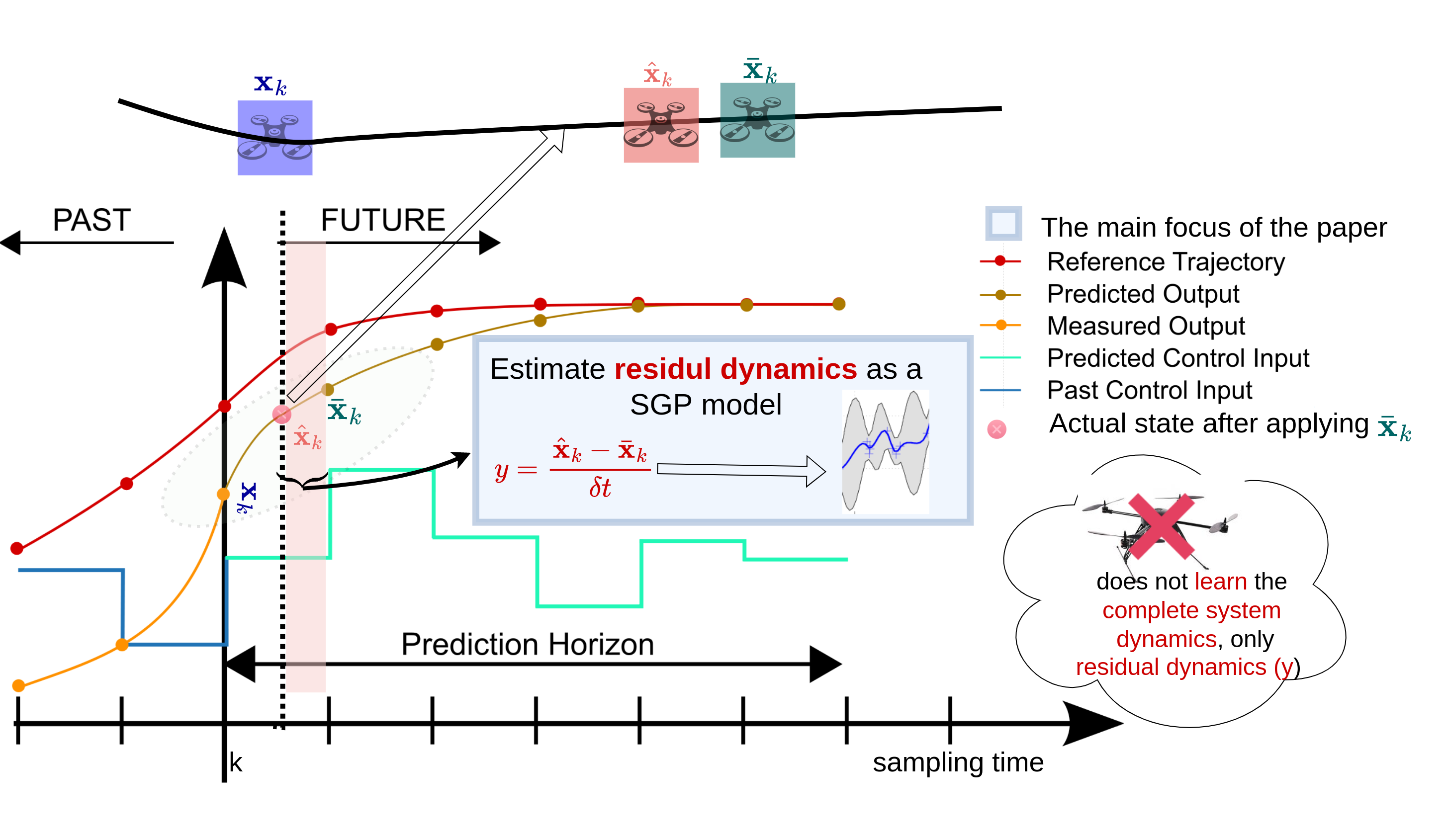
Figure 1: The high-level control command generation is based on Model Predictive Control (MPC). Residual dynamics ($y$) arise between commands generated by MPC and those executed by the flight controller. SGP-based learning estimates these dynamics.

The methodology involves integrating SGP into the nominal model to estimate and compensate for residual dynamics, particularly focusing on velocity residuals. This hybrid approach enables real-time performance suitable for low-speed maneuvering in cluttered environments without incurring high computational costs.

Sparse Gaussian Process Regression

The SGP is employed to model the residual dynamics by selecting inducing points that approximate the original training data distribution effectively. This approach drastically reduces the complexity of plotting Gaussian Processes from $O(n^3)$ to $O(nm^3)$, where $n$ is the number of original points and $m$ is the number of inducing points.

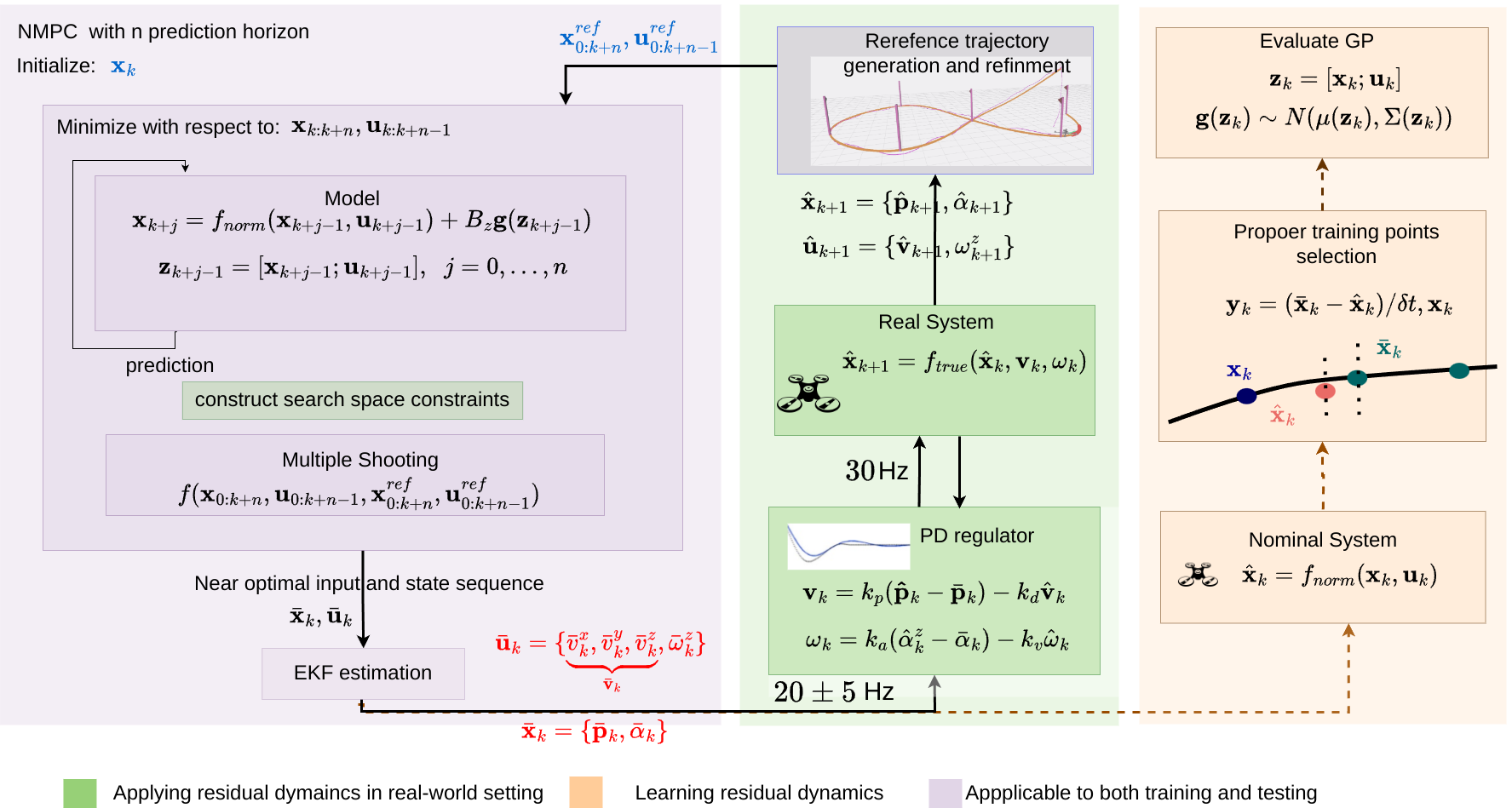
Figure 2: The high-level overview of the proposed framework for learning the residual dynamics. Design matrix $B_{\mathbf{z}}$ defines which states and inputs should be trained.

The authors provide empirical evidence indicating that fewer inducing points can sufficiently capture the residual dynamics distribution, thus optimizing the processing power without significant loss of model accuracy. This balance ensures efficient computation on embedded systems like Nvidia Xavier.

Experimental Results

Experimental evaluations in both simulated and real-world environments demonstrate the framework's effectiveness. Analysis showed that incorporating residual dynamics into the nominal model reduced root mean square error (RMSE) significantly, providing a robust enhancement to trajectory tracking.

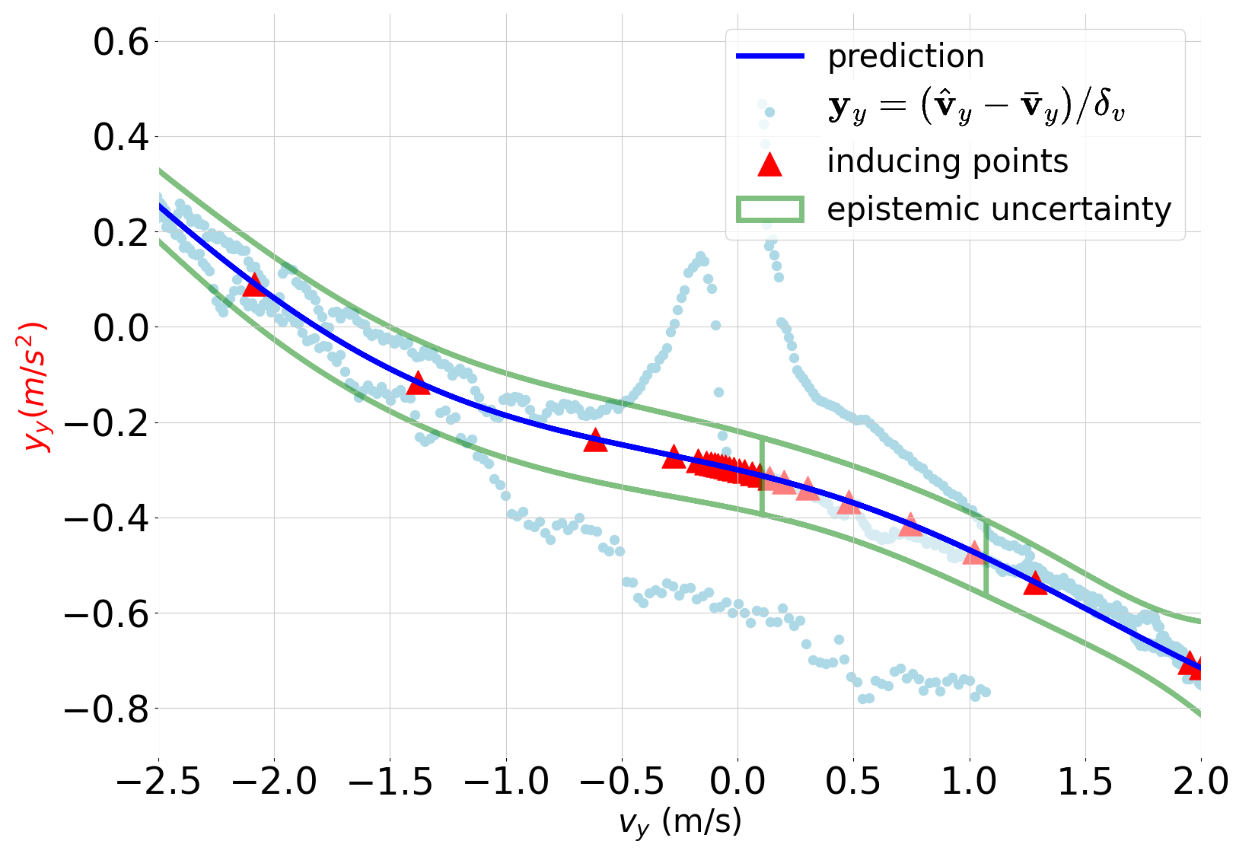
Figure 3: Epistemic uncertainty propagation of residual dynamics $\mathbf{y}$ for changing input velocity.

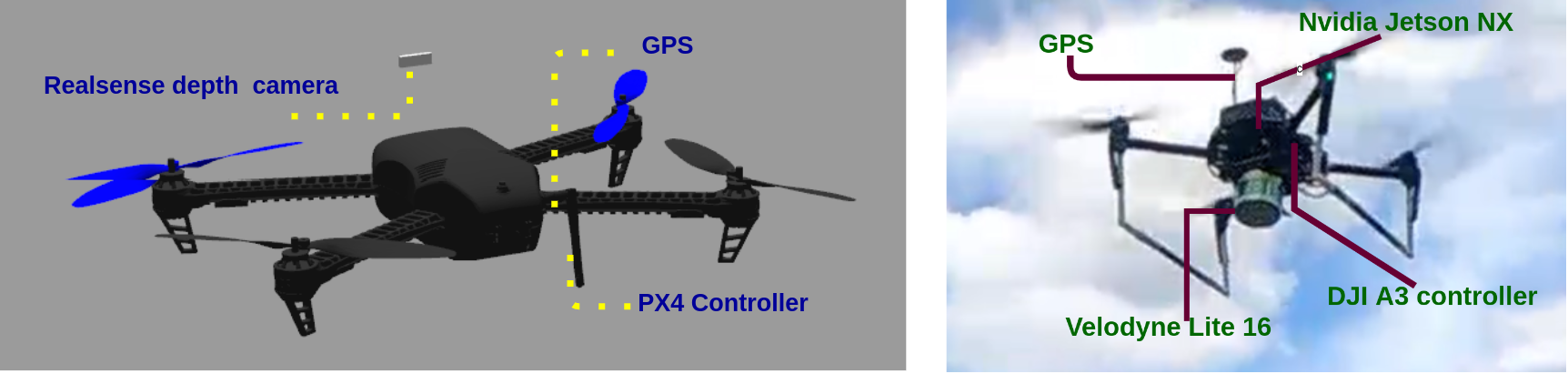
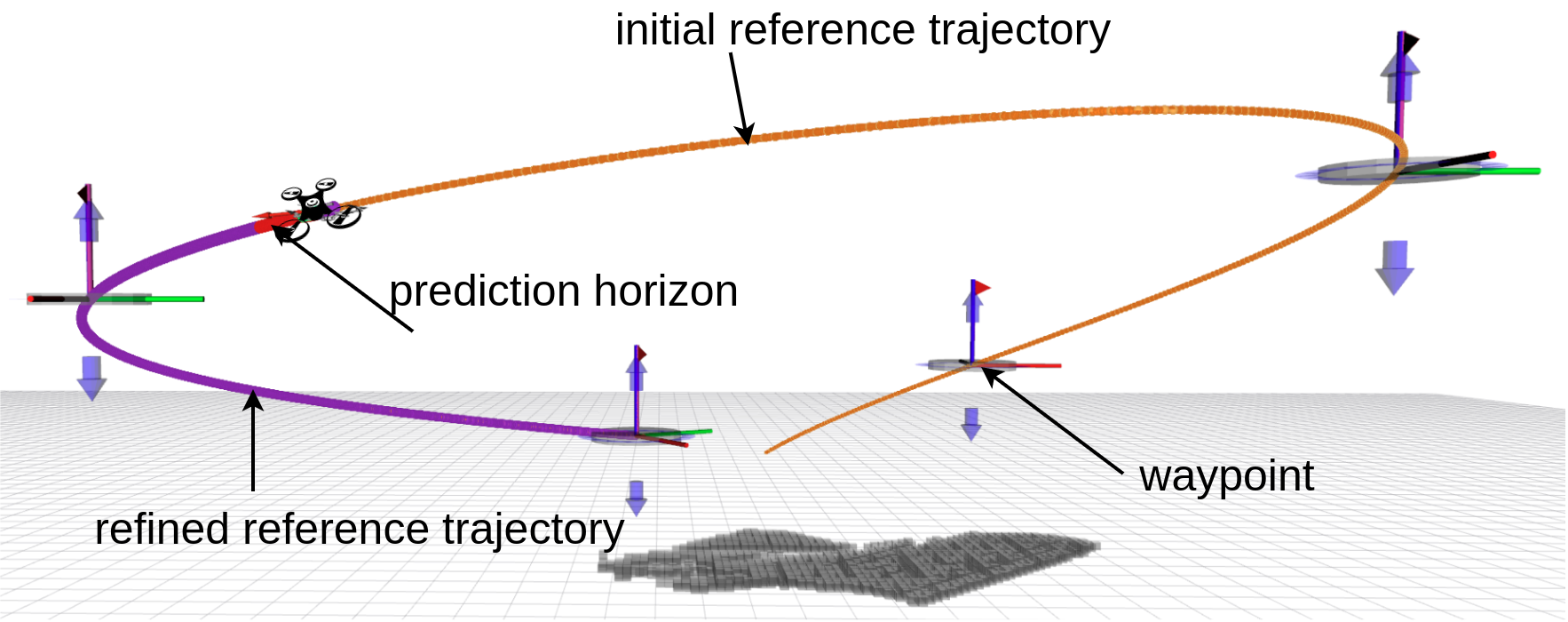
Figure 4: A motion trajectory used for data collection and testing the latent representation of residual dynamics.

The experimental setup also includes a detailed comparison of the proposed method with other trajectory tracking approaches. The experiments highlight the increased success rate in achieving trajectory tracking goals, showcasing the model's robustness to dynamic environmental constraints.

Practical Implications

This research has significant practical implications for unmanned aerial vehicle (UAV) operations in constrained environments. By addressing residual dynamics through SGP, the framework enables UAVs to maintain accurate trajectory tracking and optimize computational resources efficiently. This advancement positions the strategy as a viable option for deploying UAVs in varied fields requiring precision navigation such as agriculture, surveillance, and exploration.

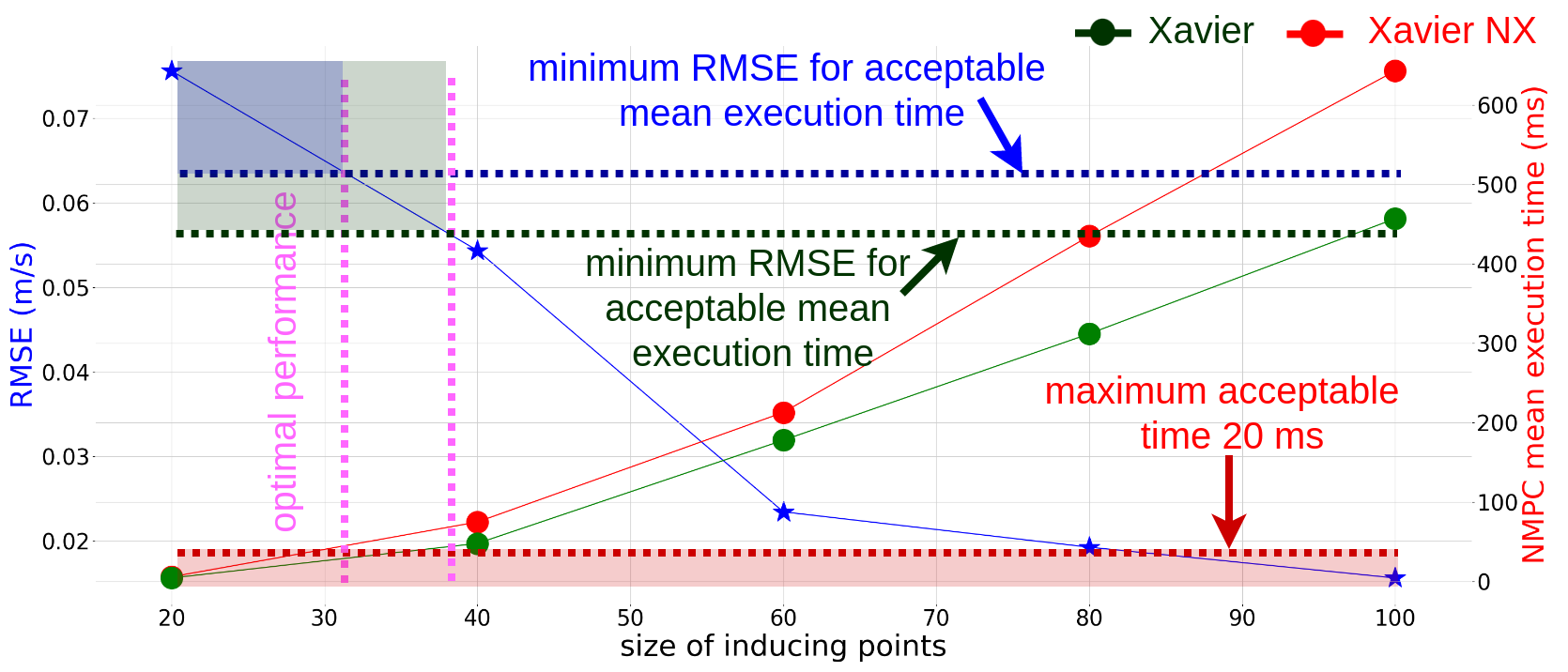
Figure 5: The relationship between residual dynamics $\mathbf{y}$ and computation power relative to inducing points.

Conclusion

The paper presents a robust approach for incorporating learned residual dynamics into trajectory tracking for multi-rotor aerial vehicles. This method substantially improves tracking performance and computational efficiency in cluttered environments. Future research could extend this framework to cater to high-speed maneuvers by integrating adaptive dynamic models. Such enhancements could further broaden the application scope of UAV systems, making them more adaptable to various real-world challenges.