Testing the General Deductive Reasoning Capacity of Large Language Models Using OOD Examples (2305.15269v3)

Abstract: Given the intractably large size of the space of proofs, any model that is capable of general deductive reasoning must generalize to proofs of greater complexity. Recent studies have shown that LLMs possess some abstract deductive reasoning ability given chain-of-thought prompts. However, they have primarily been tested on proofs using modus ponens or of a specific size, and from the same distribution as the in-context examples. To measure the general deductive reasoning ability of LLMs, we test on a broad set of deduction rules and measure their ability to generalize to more complex proofs from simpler demonstrations from multiple angles: depth-, width-, and compositional generalization. To facilitate systematic exploration, we construct a new synthetic and programmable reasoning dataset that enables control over deduction rules and proof complexity. Our experiments on four LLMs of various sizes and training objectives show that they are able to generalize to compositional proofs. However, they have difficulty generalizing to longer proofs, and they require explicit demonstrations to produce hypothetical subproofs, specifically in proof by cases and proof by contradiction.

• The paper demonstrates that LLMs can generalize deductive reasoning across varied logical rules using a synthetic OOD dataset.
• It shows that in-context examples greatly affect performance, with models excelling in simpler cases but facing challenges with increased complexity.
• Results indicate that strategic selection of examples and model pre-training enhancements are key for improving logical inference in LLMs.

Testing the General Deductive Reasoning Capacity of LLMs Using OOD Examples

Introduction

The paper investigates the capacity of LLMs to generalize their deductive reasoning to out-of-distribution (OOD) examples. LLMs, such as GPT-3.5 and PaLM, have demonstrated some ability in abstract deductive reasoning when given chain-of-thought (CoT) prompts. However, these models have largely been tested on proofs of limited complexity and size, typically leveraging modus ponens within the same distribution as in-context examples. This paper aims to assess LLMs' generalization across various deduction rules, proof depths, and widths, using a newly developed synthetic dataset, PrOntoQA-OOD.

Methodology

Dataset Construction: The PrOntoQA-OOD dataset is synthetic, allowing precise control over deduction rules and proof complexity. It extends prior datasets by incorporating a complete set of deduction rules from propositional logic, including conjunction, disjunction, and proof by contradiction.

Evaluation Method: Proofs are evaluated through semantic parsing into first-order logic to ensure that each step follows valid deductive rules. The framework assesses whether LLMs can apply these rules without explicit demonstrations, indicative of true generalization capabilities.

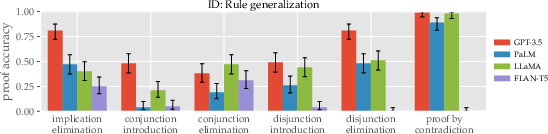
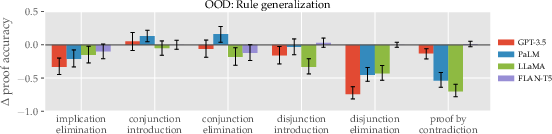
Figure 1: Proof accuracy across different deduction rules, with comparisons between in-context and OOD test scenarios.

Results

Deduction Rule Generalization: LLMs show varying ability to adapt to different logical rules without explicit training. While conjunction and disjunction rules saw reasonable generalization, proof by contradiction and disjunction elimination required more explicit demonstration.

Compositional Proofs: Models like GPT-3.5 could handle compositional proofs involving multiple deduction rules but exhibited limitations when the complexity and proof types increased. Interestingly, models often performed better with diverse, rule-specific in-context examples rather than those closely mirroring test distributions.

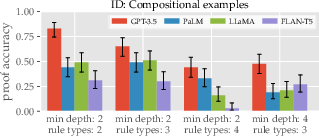
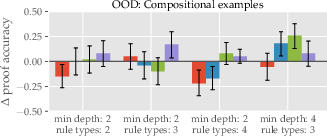
Figure 2: Compositional ID and OOD proof accuracy, highlighting the impact of rule diversity in in-context examples.

Depth and Width Generalization: The paper found that inference capabilities diminish with complexity beyond demonstrated examples. Marginal improvements in some tasks suggest better performance with simpler, more varied in-context examples.

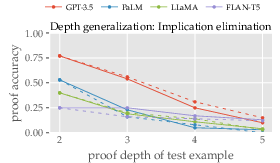
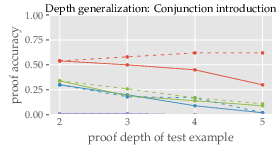
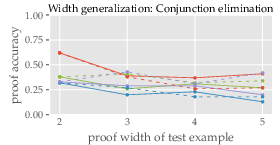
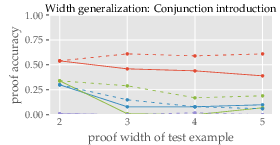
Figure 3: Proof accuracy vs. depth and width, illustrating diminishing returns with increased complexity.

Discussion

The results advance understanding of how LLMs learn from in-context examples and suggest that diverse and strategically selected examples can enhance OOD reasoning. The findings challenge existing theories that suggest in-context learning mimics gradient descent, offering evidence that practical application of learned deduction may often require a more nuanced selection of examples than previously theorized.

Conclusion

This paper underscores the need for careful selection of in-context examples to maximize the reasoning capacity of LLMs in OOD settings. Although current models show some versatility in reasoning, extending beyond explicit examples remains a challenge. Future developments could focus on refining in-context learning strategies and enhancing model pre-training to better internalize a wider range of logical structures.

In conclusion, while LLMs demonstrate some ability to extrapolate and apply reasoning to complex, unseen examples, this capacity is sensitive to the nature of in-context examples and deductive rule familiarity. These insights open pathways for improving LLM architectures and training paradigms to foster more robust generalization in deductive reasoning tasks.