Learning Neural PDE Solvers with Parameter-Guided Channel Attention (2304.14118v2)

Abstract: Scientific Machine Learning (SciML) is concerned with the development of learned emulators of physical systems governed by partial differential equations (PDE). In application domains such as weather forecasting, molecular dynamics, and inverse design, ML-based surrogate models are increasingly used to augment or replace inefficient and often non-differentiable numerical simulation algorithms. While a number of ML-based methods for approximating the solutions of PDEs have been proposed in recent years, they typically do not adapt to the parameters of the PDEs, making it difficult to generalize to PDE parameters not seen during training. We propose a Channel Attention mechanism guided by PDE Parameter Embeddings (CAPE) component for neural surrogate models and a simple yet effective curriculum learning strategy. The CAPE module can be combined with neural PDE solvers allowing them to adapt to unseen PDE parameters. The curriculum learning strategy provides a seamless transition between teacher-forcing and fully auto-regressive training. We compare CAPE in conjunction with the curriculum learning strategy using a popular PDE benchmark and obtain consistent and significant improvements over the baseline models. The experiments also show several advantages of CAPE, such as its increased ability to generalize to unseen PDE parameters without large increases inference time and parameter count.

• The paper introduces Cape, a parameter-guided channel attention module that enhances neural PDE solvers by integrating PDE parameter embeddings.
• It employs a blend of convolution types modulated by attention masks, significantly reducing prediction errors on 1D Advection, Burgers, and 2D Navier-Stokes equations.
• The curriculum learning strategy transitions from teacher-forcing to autoregressive training, improving model robustness and stability.

Learning Neural PDE Solvers with Parameter-Guided Channel Attention

Introduction

Learning Partial Differential Equations (PDEs) with machine learning models is central to advancing scientific computing, particularly in fields requiring the simulation of complex physical systems. Traditional numerical methods, while effective, are computationally expensive and often non-differentiable. This paper introduces a Parameter-Guided Channel Attention (Cape) mechanism designed to enhance neural surrogates' ability to generalize across varied PDE parameters. By employing a channel-attention module, Cape facilitates the robust integration of PDE parameter information into the surrogate models.

Methodology: Cape Framework

The Cape module is designed as an adaptable component that can be integrated into existing autoregressive neural PDE solvers without modifying their base architecture. Central to Cape's effectiveness is the channel-attention mechanism guided by PDE parameter embeddings. This approach supports the generation of intermediate time-step estimates, improving the learning model's ability to adapt to previously unseen PDE parameters.

The module uses three different types of convolutions: 1x1, depth-wise, and spectral, which interpret the partial derivative terms of the PDEs using a finite difference-like approach. Attention masks, computed via a multi-layer perceptron (MLP), modulate these convolutions in relation to specific PDE parameters.

Figure 1: The standard autoregressive approach (left) and the proposed Cape approach (right) which consists of two interdependent steps.

Figure 2: The Cape module for one type of convolution (residual connections are omitted).

Curriculum Learning Strategy

The paper proposes a curriculum learning strategy to bridge the gap between teacher-forcing and autoregressive training methodologies. This strategy transitions gradually from using true input sequences (teacher-forcing) to the model's generated predictions (autoregressive), thereby improving the model's stability and robustness throughout the learning process.

Figure 3: The proposed curriculum learning strategy leads to a smooth transition between one time-step learning ({\it teacher-forcing}).

Experimental Setup and Results

The Cape module was assessed using several PDE datasets: 1D Advection, 1D Burgers, and 2D Compressible Navier-Stokes equations. The experiments demonstrated Cape's ability to significantly reduce predictive errors across various parameter conditions, showcasing its generalization capabilities to dynamically varying physical systems.

Key Results:

• 1D Advection: Cape achieves a major reduction in RMSE compared to baseline models, validating its efficacy in processing advection-dominant phenomena.
• 1D Burgers' Equation: Demonstrated significant improvement in modeling diffusion processes.
• 2D Navier-Stokes: Cape outperformed conventional neural PDE solvers in capturing multi-dimensional flow dynamics.

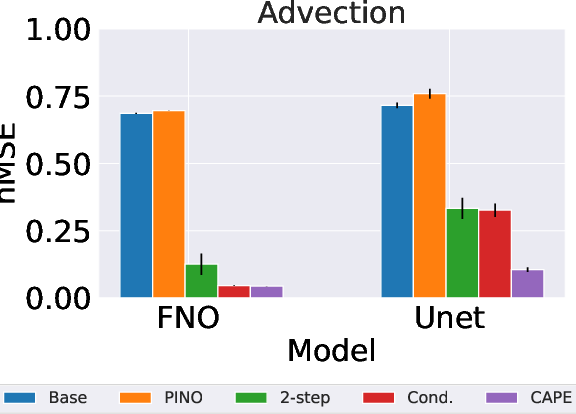
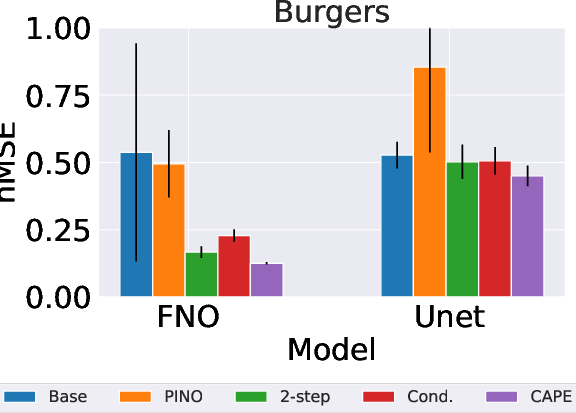
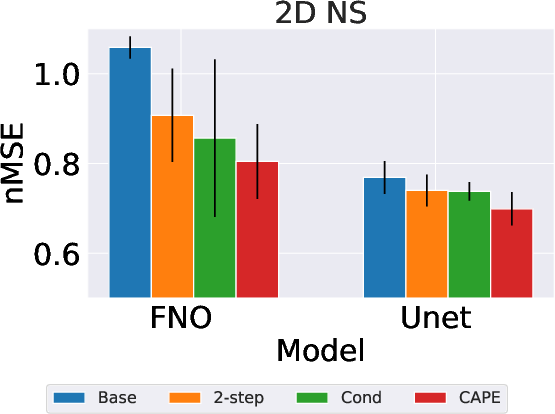
Figure 4: Plots of the normalized MSE (smaller is better) with an error bar for Advection eq. (Left), Burgers eq. (Middle), and 2D Compressible NS equations (Right).

Qualitative Analysis and Visualization

Cape's ability to provide high-frequency proposals to the base network enhances predictive accuracy, as evidenced through qualitative visualization. The attention mechanisms inherent within Cape allow it to adjust dynamically, improving the resolution of PDE solutions.

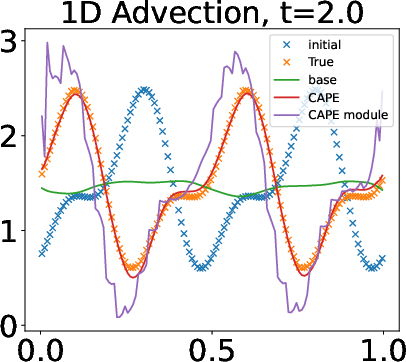
Figure 5: Visualization of the results: Advection eq. at the final time-step (t=2.0) (Left), Burgers eq. at t_k = 20 (t=1.0) (2nd-left) at the final time-step, and V_x of 2D NS equations at t_k=5 (t=0.25) (Right).

Conclusion

The Cape module's design enables neural PDE solvers to generalize effectively across different PDE parameter regimes while remaining computationally efficient. The curriculum learning strategy bridges the stability gap inherent in autoregressive training, enhancing the real-world applicability of neural surrogate models in scientific domains.

Future Work

Moving forward, it is critical to further explore the role of Cape in more complex, real-world applications beyond the scope defined within this paper. Specifically, applying Cape to inherently multidimensional and non-linear PDE systems, such as those found in meteorological and climate predictions, represents a promising avenue for research and application.

In summary, Cape provides a robust mechanism for integrating parameter-guided attention into neural PDE solvers, significantly enhancing their accuracy and generalization capabilities while maintaining efficiency.