A Simple Explanation for the Phase Transition in Large Language Models with List Decoding (2303.13112v1)

Abstract: Various recent experimental results show that LLMs (LLM) exhibit emergent abilities that are not present in small models. System performance is greatly improved after passing a certain critical threshold of scale. In this letter, we provide a simple explanation for such a phase transition phenomenon. For this, we model an LLM as a sequence-to-sequence random function. Instead of using instant generation at each step, we use a list decoder that keeps a list of candidate sequences at each step and defers the generation of the output sequence at the end. We show that there is a critical threshold such that the expected number of erroneous candidate sequences remains bounded when an LLM is below the threshold, and it grows exponentially when an LLM is above the threshold. Such a threshold is related to the basic reproduction number in a contagious disease.

• The paper provides a simple theoretical explanation for the phase transition in LLMs using a sequence-to-sequence random model with list decoding, pinpointing a critical threshold at Mε=1.
• It introduces the concept of ε-compatible LLMs, ensuring that the oracle sequence remains in the candidate set to maintain bounded error propagation.
• The analysis links model scaling with error dynamics, offering actionable insights for designing more robust Transformer-based architectures.

A Simple Explanation for the Phase Transition in LLMs with List Decoding

Introduction

The paper "A Simple Explanation for the Phase Transition in LLMs with List Decoding" addresses the critical threshold phenomenon that occurs in LLMs. These models demonstrate emergent abilities not observed in smaller models, significantly enhancing performance post-threshold. This essay explicates the phase transition by modeling LLMs as sequence-to-sequence random functions with a list decoder, explaining the conditions under which candidate sequence errors remain bounded or grow exponentially.

Model and Assumptions

The investigation models an LLM using a sequence-to-sequence random function on a token space with $M$ possible tokens. The paper introduces a list decoding methodology, where a list of candidate sequences is maintained throughout the sequence generation process. This approach contrasts with traditional autoregressive models that select tokens instantaneously. The list decoder defers the output sequence generation until the end, allowing a more robust evaluation and selection process.

Theoretical Analysis

List Decoding with Candidate Sets

The list decoding process involves classifying tokens at each step as either eligible or not, as dictated by a binary classifier. This method allows for maintaining a candidate set, enhancing robustness against cascading errors from incorrect token selections. The paper describes an oracle model that always generates the correct sequence, serving as a performance benchmark for $\epsilon$-compatible LLMs.

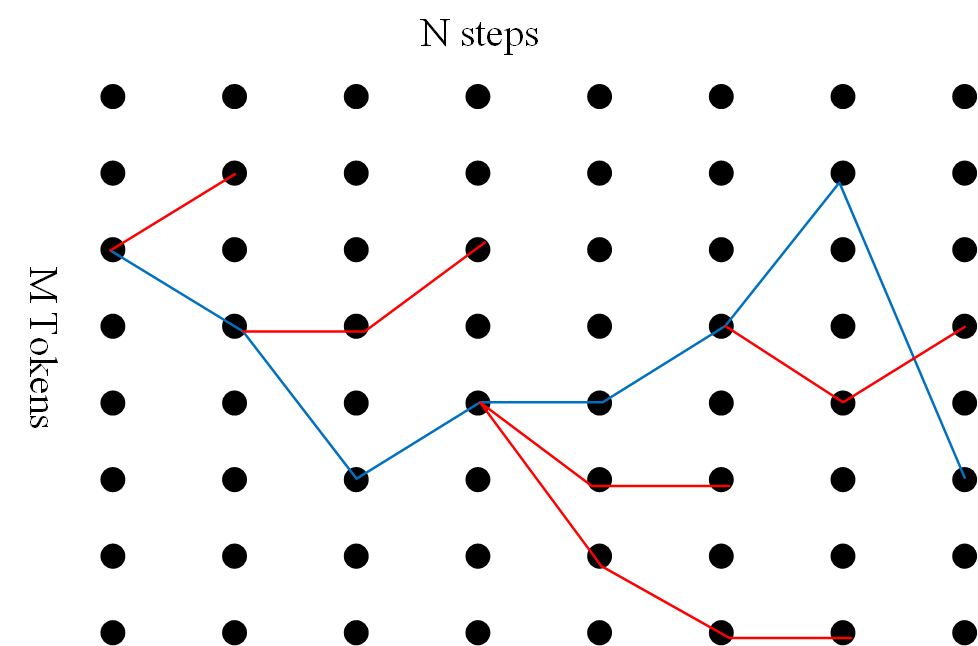
Figure 1: Illustration of candidate set evolution with the oracle sequence in blue and erroneous sequences in red.

$\epsilon$-Compatible LLMs

An LLM is $\epsilon$-compatible if it (1) includes the oracle-generated sequence in every candidate set, ensuring 100% recall, and (2) maintains a bounded false alarm probability per step. These conditions ensure that erroneous sequences remain limited if $M \epsilon < 1$.

Phase Transition and Critical Threshold

The paper establishes a critical threshold condition at $M \epsilon = 1$. If the false alarm product $M \epsilon$ is less than 1, the expected erroneous sequences remain bounded, presaging a high probability of the model reproducing the oracle's output. Conversely, if $M \epsilon > 1$, errors proliferate exponentially across steps. This analogous behavior to the basic reproduction number in epidemiology denotes the phase transition point, distinguishing between regime behaviors in LLMs.

Conclusions

The phase transition in LLMs is a pivotal concept for understanding performance scaling. By harnessing list decoding and modeling $\epsilon$-compatibility, the paper outlines how model scaling influences error boundaries, informing more efficient LLM deployments. The critical threshold $M \epsilon = 1$ provides a key metric for designing and scaling LLMs to optimize deployment in NLP tasks.

This analysis emphasizes that extending list decoding into probabilistic evaluation could refine sequences generated by LLMs, paving pathways for enhanced Transformer-based architectures in future research endeavors.