Revisiting Weighted Strategy for Non-stationary Parametric Bandits (2303.02691v2)

Abstract: Non-stationary parametric bandits have attracted much attention recently. There are three principled ways to deal with non-stationarity, including sliding-window, weighted, and restart strategies. As many non-stationary environments exhibit gradual drifting patterns, the weighted strategy is commonly adopted in real-world applications. However, previous theoretical studies show that its analysis is more involved and the algorithms are either computationally less efficient or statistically suboptimal. This paper revisits the weighted strategy for non-stationary parametric bandits. In linear bandits (LB), we discover that this undesirable feature is due to an inadequate regret analysis, which results in an overly complex algorithm design. We propose a refined analysis framework, which simplifies the derivation and importantly produces a simpler weight-based algorithm that is as efficient as window/restart-based algorithms while retaining the same regret as previous studies. Furthermore, our new framework can be used to improve regret bounds of other parametric bandits, including Generalized Linear Bandits (GLB) and Self-Concordant Bandits (SCB). For example, we develop a simple weighted GLB algorithm with an $\widetilde{O}(k_μ^{\frac{5}{4}} c_μ^{-\frac{3}{4}} d^{\frac{3}{4}} P_T^{\frac{1}{4}}T^{\frac{3}{4}})$ regret, improving the $\widetilde{O}(k_μ^{2} c_μ^{-1}d^{\frac{9}{10}} P_T^{\frac{1}{5}}T^{\frac{4}{5}})$ bound in prior work, where $k_μ$ and $c_μ$ characterize the reward model's nonlinearity, $P_T$ measures the non-stationarity, $d$ and $T$ denote the dimension and time horizon.

• The paper presents a new weighted strategy for non-stationary parametric bandits that employs a single covariance matrix for efficient estimation.
• It demonstrates improved regret bounds of O(d^(3/4) P_T^(1/4) T^(3/4)) for linear bandits, surpassing previous computational and statistical methods.
• Extensions to generalized linear and self-concordant bandits illustrate the approach's robustness and potential for adaptive, real-world applications.

Revisiting Weighted Strategy for Non-stationary Parametric Bandits

The paper "Revisiting Weighted Strategy for Non-stationary Parametric Bandits" (2303.02691) presents a refined framework for analyzing and implementing weighted strategies in non-stationary parametric bandit problems. The authors develop a simpler and more efficient approach that aligns with standard sliding-window and restart strategies while achieving comparable or superior regret bounds.

Introduction

Bandit problems in non-stationary environments necessitate strategies that adapt to time-varying reward distributions. The paper addresses the limitations of previous weighted strategies that were computationally inefficient or statistically suboptimal. By refining the regret analysis framework, the authors introduce a new weighted strategy that is as efficient as existing window or restart-based strategies, yet retains favorable regret bounds.

Linear Bandits

Problem Setting

In the context of Linear Bandits (LB), the expected reward for selecting an arm is modeled as the inner product of the arm's feature vector and an unknown time-varying parameter. The goal is to minimize dynamic regret, the difference between the cumulative reward of the optimal strategy and the learner's strategy.

Algorithm and Analysis

The proposed \texttt{LBweightours} algorithm employs a weighted regularized least square estimator. The crucial novelty lies in using a single covariance matrix for the estimator, reducing computational complexity compared to prior approaches that required multiple covariance matrices.

\begin{equation} r_t = X_t^\T\theta_t + \eta_t, \end{equation}

where $r_t$ is the reward, $\theta_t$ is the unknown parameter, and $\eta_t$ represents noise. The algorithm calculates the estimator $\thetah_t$ using:

\begin{equation} \thetah_t = V_{t-1}^{-1}(\sum_{s=1}^{t-1}\gamma^{t-s-1}r_sX_s). \end{equation}

This approach achieves a regret bound of $\Ot(d^{3/4} P_T^{1/4} T^{3/4})$, improving prior results dependent on dimensional assumptions.

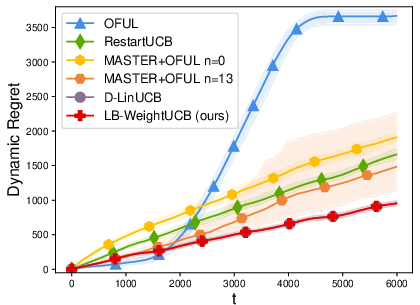
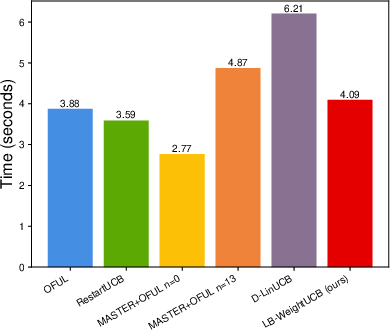
Figure 1: Experiments of linear bandits.

Generalized Linear Bandits

The framework extends to Generalized Linear Bandits (GLB), where rewards follow a generalized linear model with a time-varying parameter. The paper's approach simplifies analysis by aligning bias and variance estimation terms under the same local norm, addressing critical limitations of prior weighted GLB algorithms.

Algorithm Improvements

The \texttt{GLBweightours} algorithm modifies the estimation process:

1. Estimator Calculation: Simplifies projections using consistent norms.
2. Theoretical Performance: Achieves improved regret bounds of $\Ot(k_\mu^{5/4} c_\mu^{-3/4} d^{3/4} P_T^{1/4} T^{3/4})$, surpassing existing algorithms while requiring less computational effort.

Self-Concordant Bandits

Problem Setting

Self-Concordant Bandits (SCB) are a subclass of GLB, suitable for handling logistic or exponential family rewards. The paper extends the weighted strategy to these bandits, offering enhanced efficiency without sacrificing theoretical guarantees.

Results and Discussion

A distinctive contribution for SCB is the introduction of novel local norms that better capture reward structure, significantly improving dependency on problem-specific constants such as $c_\mu$. The resulting algorithm is both simpler and more effective for logistic bandits, a common instance in real-world applications.

Conclusion and Future Work

The paper successfully revisits and simplifies weighted strategies for various parametric bandit models. A uniform analysis framework resolves inefficiencies seen in prior work, yielding algorithms that are theoretically robust and computationally efficient. Future research directions could include adaptive weight-based strategies that forego prior knowledge of environment non-stationarity, potentially leveraging ideas from adaptive restart algorithms.

The refined approach not only addresses theoretical gaps but also paves the way for practical applications in evolving, real-world scenarios. Future explorations may focus on integrating information-theoretic concepts to refine characterizations of gradual environmental changes further.