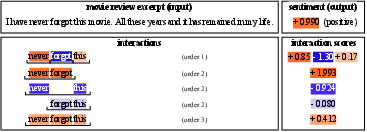SHAP-IQ: Unified Approximation of any-order Shapley Interactions (2303.01179v3)

Abstract: Predominately in explainable artificial intelligence (XAI) research, the Shapley value (SV) is applied to determine feature attributions for any black box model. Shapley interaction indices extend the SV to define any-order feature interactions. Defining a unique Shapley interaction index is an open research question and, so far, three definitions have been proposed, which differ by their choice of axioms. Moreover, each definition requires a specific approximation technique. Here, we propose SHAPley Interaction Quantification (SHAP-IQ), an efficient sampling-based approximator to compute Shapley interactions for arbitrary cardinal interaction indices (CII), i.e. interaction indices that satisfy the linearity, symmetry and dummy axiom. SHAP-IQ is based on a novel representation and, in contrast to existing methods, we provide theoretical guarantees for its approximation quality, as well as estimates for the variance of the point estimates. For the special case of SV, our approach reveals a novel representation of the SV and corresponds to Unbiased KernelSHAP with a greatly simplified calculation. We illustrate the computational efficiency and effectiveness by explaining language, image classification and high-dimensional synthetic models.

• The paper introduces SHAP-IQ, a unified sampling-based estimator for any-order Shapley interactions that provides unbiased, consistent, and computationally efficient estimates.
• It leverages a novel Cardinal Interaction Indices representation, enabling each model evaluation to update all interaction scores simultaneously and outperforming permutation- and kernel-based baselines.
• Empirical results across language, image, and synthetic models validate the method's accuracy, scalability, and interpretability, with special cases reducing to simplified forms equivalent to Unbiased KernelSHAP.

SHAP-IQ: Unified Approximation of Any-Order Shapley Interactions

The paper introduces SHAP-IQ, a unified, sampling-based estimator for efficiently approximating any-order Shapley interaction indices (CIIs) in black-box machine learning models. The approach generalizes and subsumes previous methods for Shapley-based feature interaction quantification, providing theoretical guarantees and practical improvements in computational efficiency and accuracy.

Background: Shapley Interactions and Cardinal Interaction Indices

Shapley values are widely used for feature attribution in explainable AI, quantifying the marginal contribution of individual features to a model's output. However, many real-world applications require understanding not just individual feature effects but also interactions among groups of features. Several extensions of the Shapley value to higher-order interactions have been proposed, including the Shapley Interaction Index (SII), Shapley Taylor Interaction Index (STI), and Faithful Shapley Interaction Index (FSI). Each is defined by a specific set of axioms (linearity, symmetry, dummy, efficiency, etc.) and requires a tailored approximation method.

Cardinal Interaction Indices (CIIs) provide a unifying framework for these interaction indices, as any index satisfying linearity, symmetry, and dummy axioms can be represented as a CII. However, efficient and general-purpose approximation of CIIs for arbitrary order and model class has remained an open problem due to the exponential growth in the number of feature subsets.

SHAP-IQ: Unified Sampling-Based Approximation

SHAP-IQ is built on a novel representation of CIIs, expressing the interaction score for a subset $S$ as a sum over all feature subsets $T \subseteq D$, with weights that depend only on the sizes of $T$ and $T \cap S$. This allows every model evaluation to contribute to all interaction estimates, enabling efficient simultaneous estimation of all interaction scores.

The SHAP-IQ estimator is defined as:

$$\hat I^m_{k_0}(S) = c_{k_0}(S) + \frac{1}{K} \sum_{k=1}^K \nu_0(T_k) \frac{\gamma^m_s(t_k, |T_k \cap S|)}{p_{k_0}(T_k)}$$

where $c_{k_0}(S)$ is a deterministic correction term, $T_k$ are sampled subsets, and $\gamma^m_s$ are precomputed weights. The method is unbiased, consistent, and provides explicit variance bounds.

A key advantage is that SHAP-IQ can update all interaction estimates with a single model evaluation, in contrast to permutation-based (PB) or kernel-based (KB) baselines, which are less efficient and less general. The method also allows for selective estimation of specific interactions, which is not possible with KB approaches.

Theoretical Guarantees and Special Cases

SHAP-IQ is shown to be unbiased and consistent for any CII. For the special case of the Shapley value (order $s_0=1$), SHAP-IQ yields a new, simplified representation and is equivalent to Unbiased KernelSHAP (U-KSH), but with reduced computational complexity.

The method preserves the efficiency property (the sum of interaction scores equals the total model effect) for n-SII and STI, but not for FSI, highlighting a conceptual distinction between these indices.

Empirical Evaluation

The paper presents extensive experiments on LLMs (DistilBERT for sentiment analysis), image classifiers (ResNet18 on ImageNet), and high-dimensional synthetic models (sum of unanimity models, SOUM). SHAP-IQ is compared to tailored PB and KB baselines for SII, STI, and FSI.

Key empirical findings:

• SHAP-IQ consistently outperforms PB baselines for SII and STI in terms of mean squared error (MSE) and precision at top-K interactions, especially for higher-order interactions and limited evaluation budgets.
• For FSI, KB approximation can outperform SHAP-IQ in some ML settings, but SHAP-IQ is superior in high-dimensional synthetic settings, demonstrating that no single method is universally optimal.
• SHAP-IQ's computational overhead is minimal and scales linearly with the number of model evaluations, with precomputation of weights being negligible.
• Visualization of interaction scores for real-world sentences and images demonstrates the interpretability and practical utility of SHAP-IQ in analyzing complex model behaviors.

  Figure 1: Interaction scores for a movie review excerpt presented to a sentiment analysis model.

  

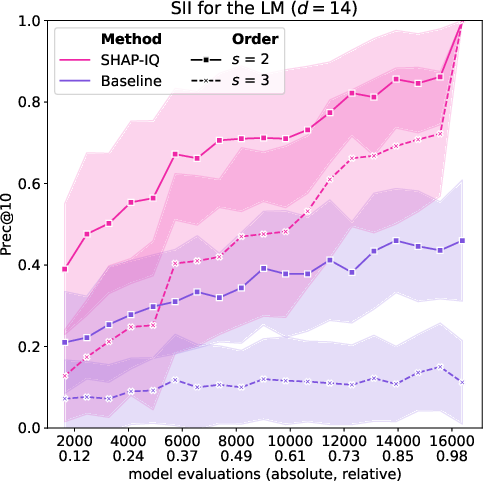
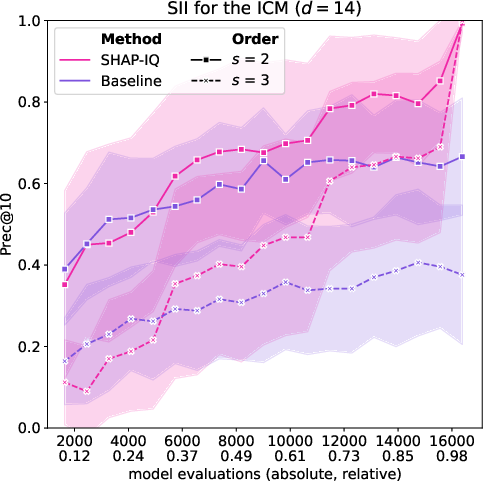
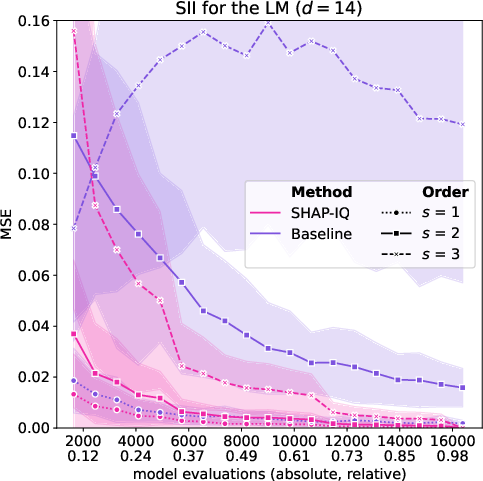
Figure 2: Approximation quality of SHAP-IQ and the baseline for orders $s=1,2,3$ of SII measured by MSE for the LM (left) and Prec@10 for orders $s=2,3$ for the LM (middle) and ICM (right).

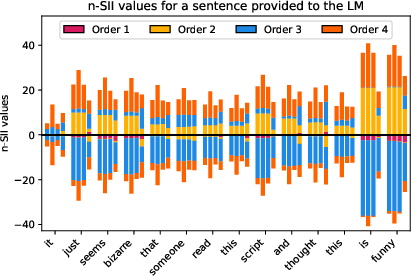
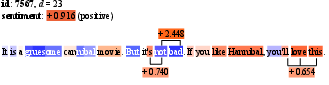
Figure 3: Visualization of n-SII and $s_0=4$ for a movie review, showing the distribution of interaction effects across words.

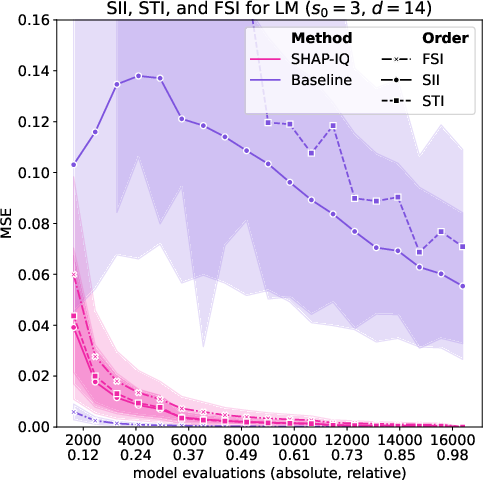
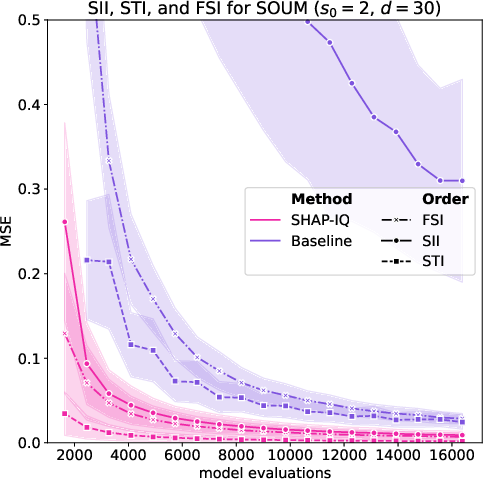
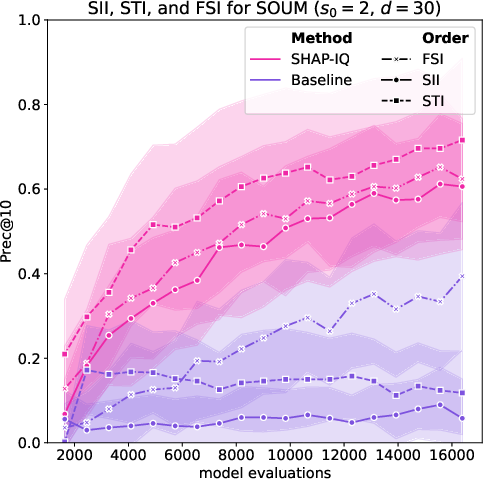
Figure 4: Approximation quality for top-order interactions of SII, STI, and FSI of the LM with $s_0 = 3$ (left) and the SOUM with $s_0=2$ (middle and right).

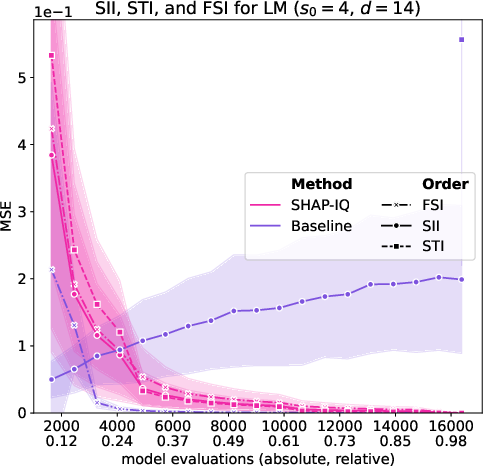
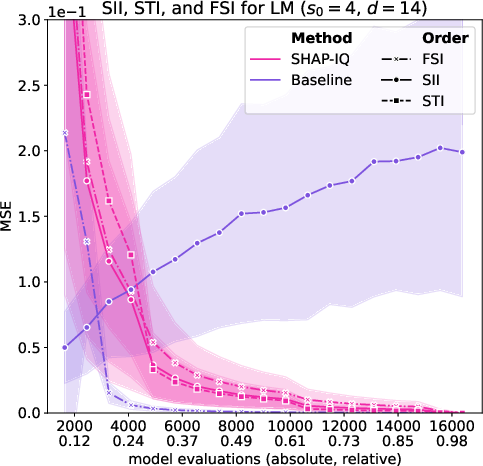
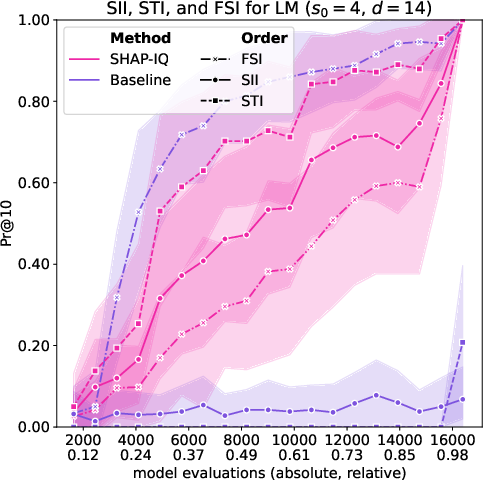
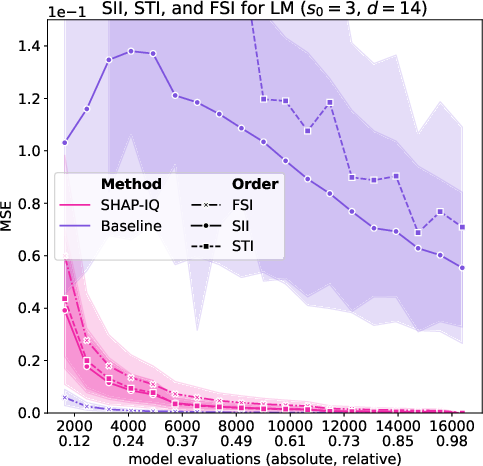
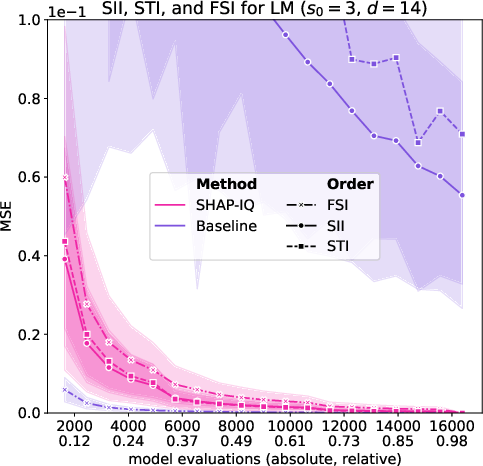
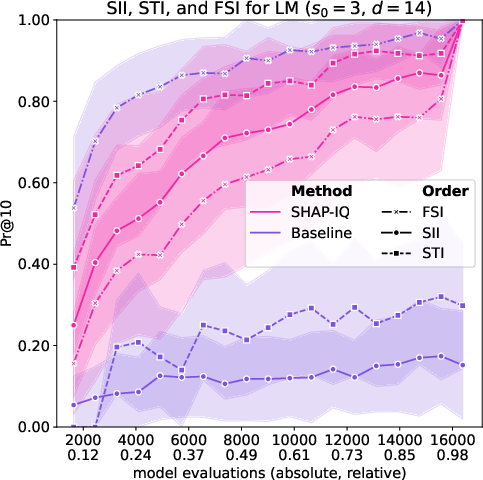
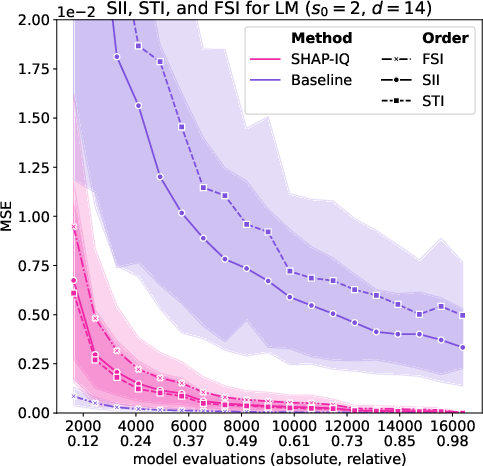
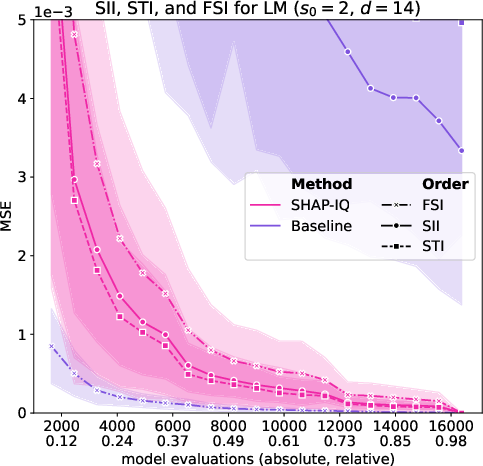
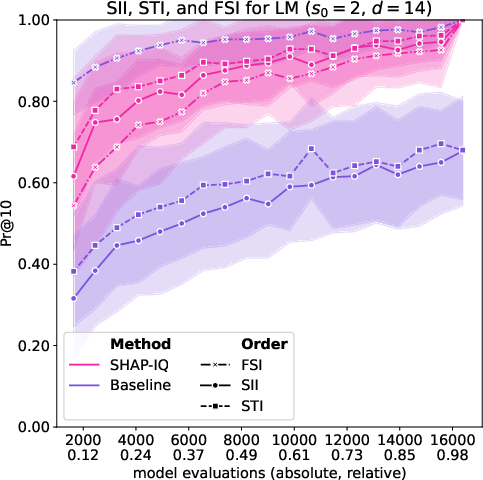
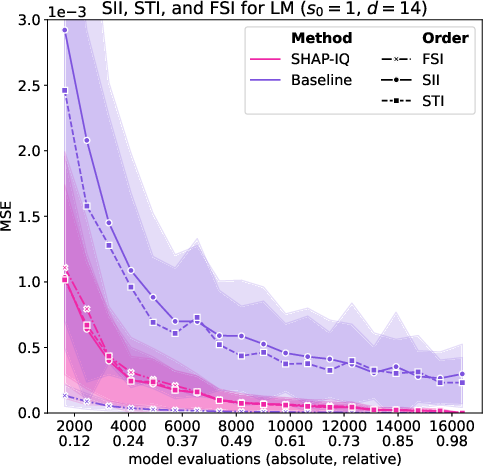
Figure 5: Approximation Quality for LM with interaction order $s_0 = 4$ for $g = 50$ iterations (first row), with interaction order $s_0 = 3$ for $g = 50$ iterations (second row), with interaction order $s_0 = 2$ for $g = 50$ iterations (third row), and with interaction order $s_0 = 1$ (Shapley Value) for $g = 50$ iterations (fourth row).

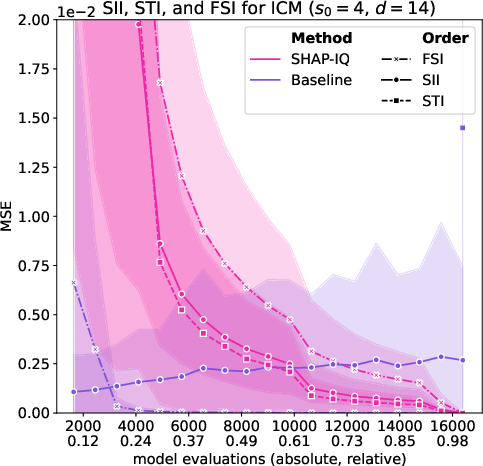
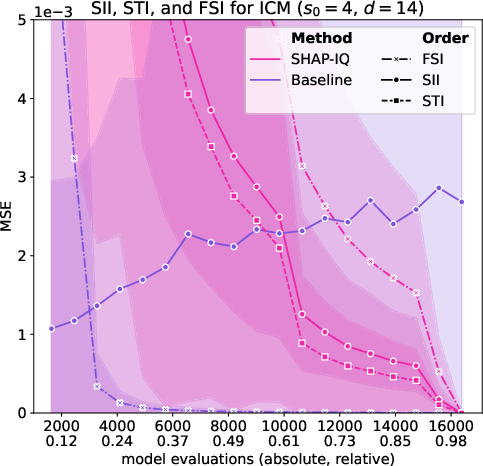
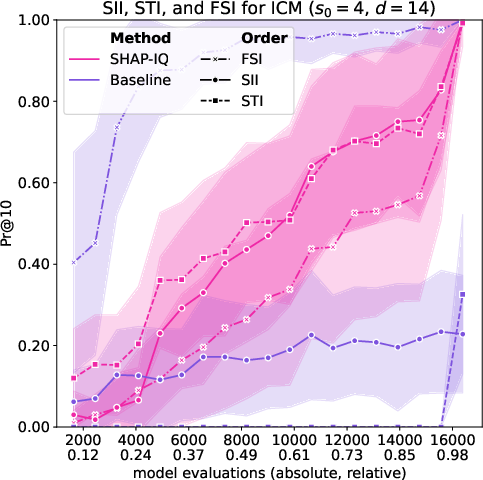
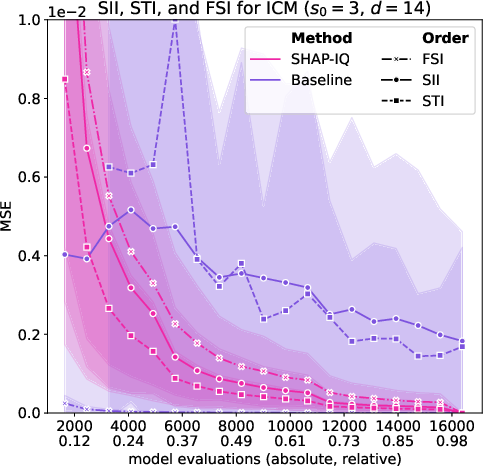
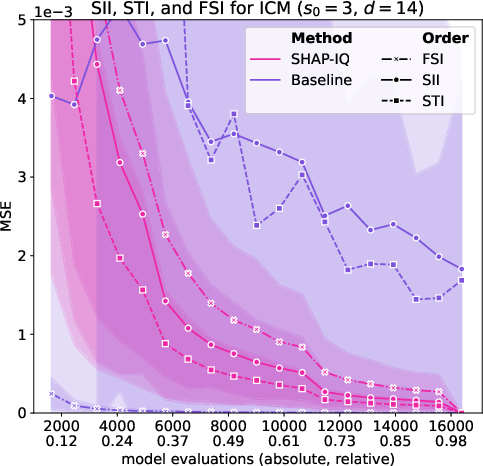
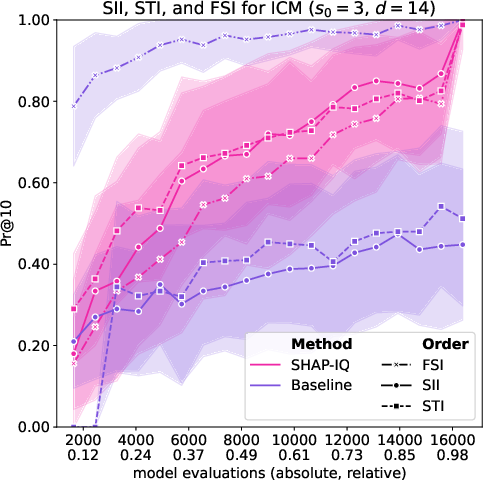
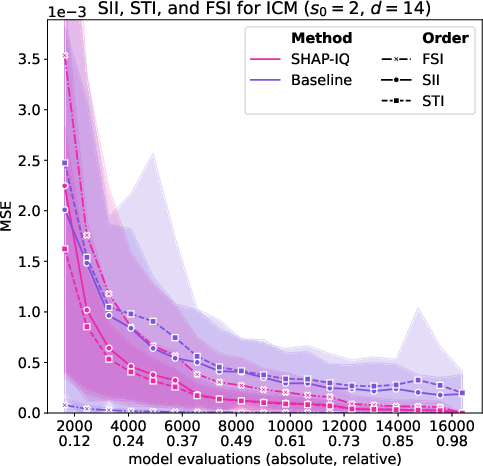
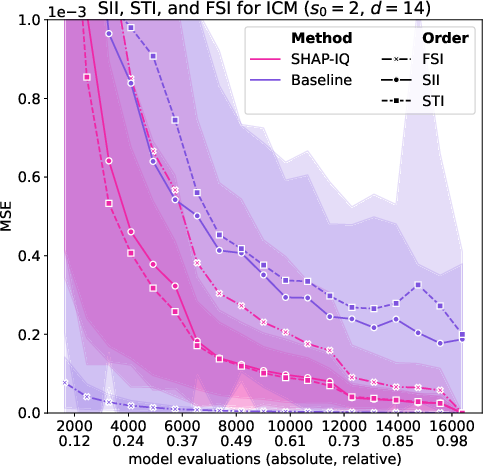
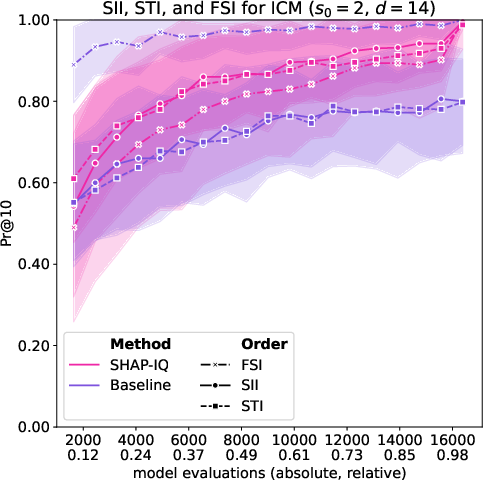
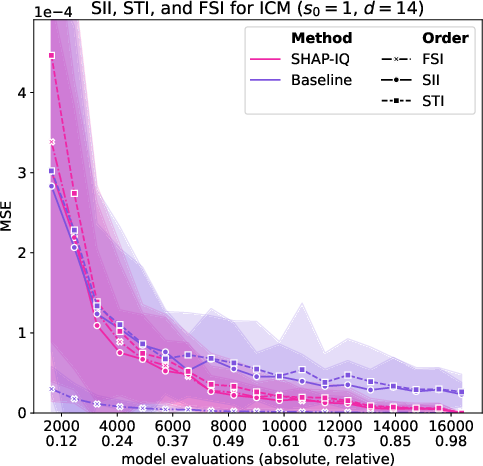
Figure 6: Approximation Quality for ICM with interaction order $s_0 = 4$ for $g = 50$ iterations (first row), with interaction order $s_0 = 3$ for $g = 50$ iterations (second row), with interaction order $s_0 = 2$ for $g = 50$ iterations (third row), and with interaction order $s_0 = 1$ (Shapley Value) for $g = 50$ iterations (fourth row).

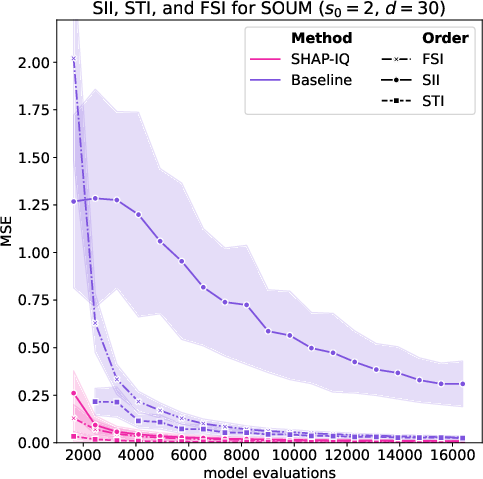
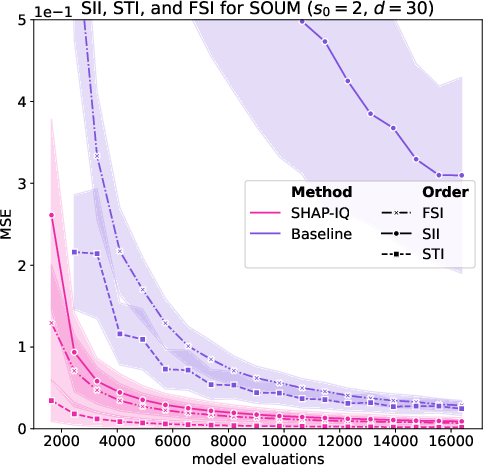
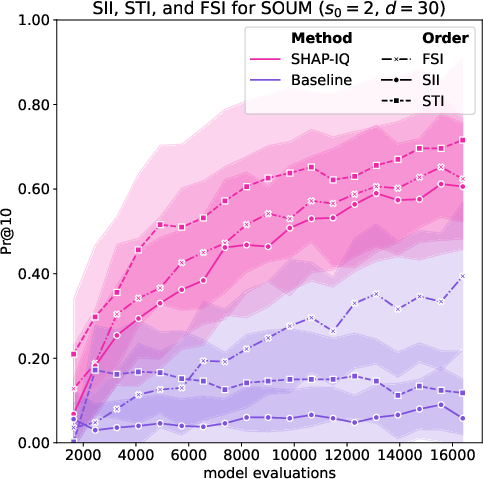
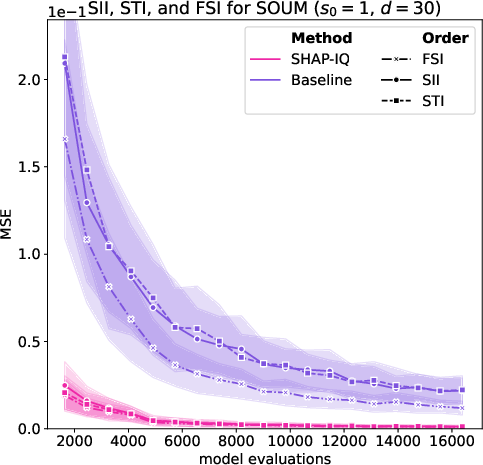
Figure 7: Approximation Quality for SOUM order $s_0 = 2$ (first row) and $s_0 = 1$ (Shapley value, second row) for $g = 50$ iterations on the SOUM with $N = 100$ interactions, $d = 30$ features.

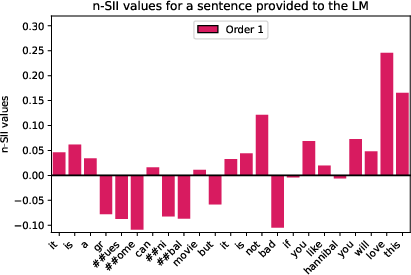
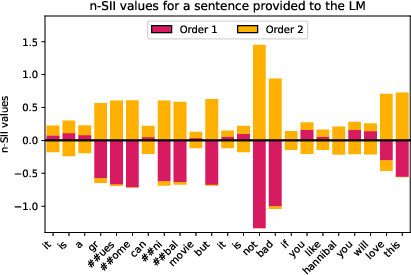
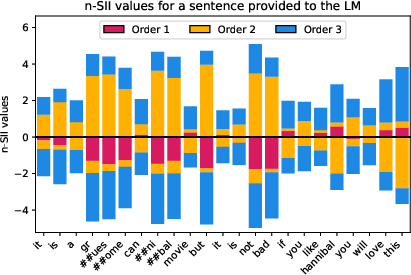
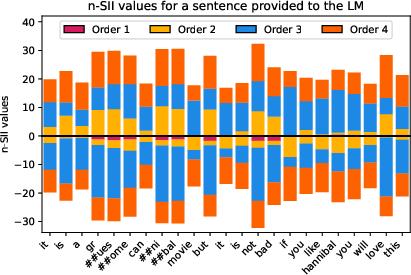
Figure 8: Estimated SII values with orders $s=1,2,3,4$ for the sentence ``It is a gruesome cannibal movie. But it's not bad. If you like Hannibal, you'll love this.'' ($d = 23$) provided to the LM.

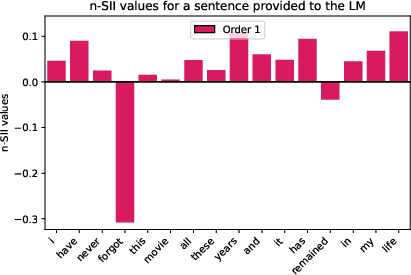
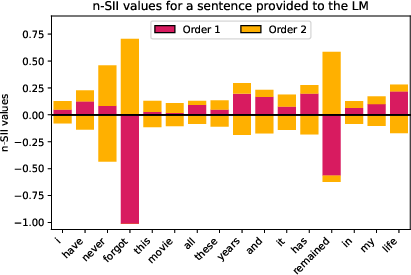
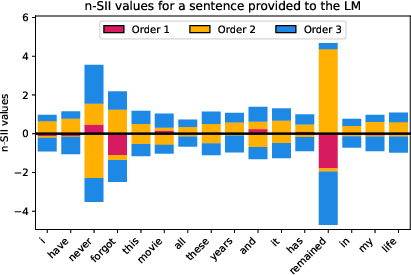
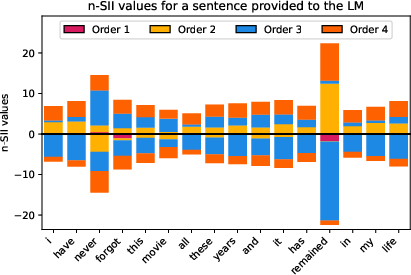
Figure 9: Estimated SII values with orders $s=1,2,3,4$ for the sentence ``I have never forgot this movie. All these years and it has remained in my life.'' ($d = 16$) provided to the LM.

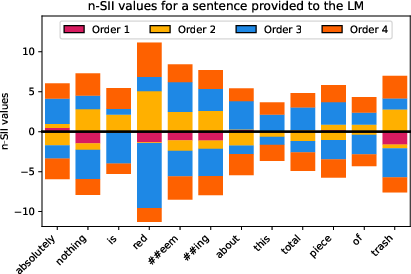
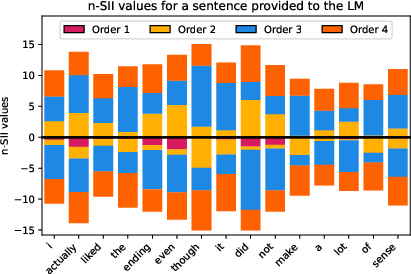
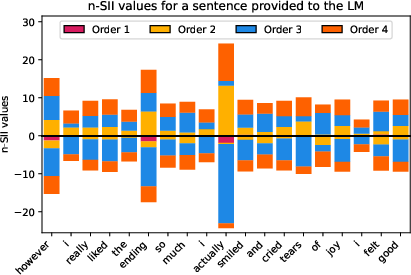
Figure 10: Estimated n-SII values with $s_0=4$ for four different sentences provided to the LM.

Limitations

SHAP-IQ is applicable to any interaction index that admits a CII representation, i.e., satisfies linearity, symmetry, and dummy axioms. For FSI, closed-form representations for lower-order interactions are not available, limiting SHAP-IQ to top-order FSI interactions. The method is model-agnostic and does not exploit model structure (e.g., trees, linearity), so further efficiency gains may be possible for specific model classes.

Implications and Future Directions

SHAP-IQ provides a theoretically grounded, general-purpose tool for quantifying feature interactions of arbitrary order in black-box models. This enables more comprehensive model interpretability, especially in domains where interactions are critical (e.g., genomics, NLP, drug discovery). The method's statistical properties (unbiasedness, variance estimation) facilitate rigorous uncertainty quantification.

Future work should address:

• Extension to model-specific variants (e.g., TreeSHAP for interactions)
• Scalable post-processing and visualization for high-order interactions
• Integration with human-in-the-loop systems for interpretability
• Sequential and adaptive sampling strategies for improved efficiency
• Application to large-scale real-world problems in science and engineering

Conclusion

SHAP-IQ advances the state of the art in Shapley-based interaction quantification by providing a unified, efficient, and theoretically justified estimator for any-order CIIs. It outperforms existing baselines in both accuracy and computational efficiency for a wide range of models and interaction indices. The approach enables practical, interpretable analysis of complex feature interactions in modern machine learning systems, with broad implications for explainable AI and scientific discovery.