Incorporating Background Knowledge in Symbolic Regression using a Computer Algebra System (2301.11919v2)

Abstract: Symbolic Regression (SR) can generate interpretable, concise expressions that fit a given dataset, allowing for more human understanding of the structure than black-box approaches. The addition of background knowledge (in the form of symbolic mathematical constraints) allows for the generation of expressions that are meaningful with respect to theory while also being consistent with data. We specifically examine the addition of constraints to traditional genetic algorithm (GA) based SR (PySR) as well as a Markov-chain Monte Carlo (MCMC) based Bayesian SR architecture (Bayesian Machine Scientist), and apply these to rediscovering adsorption equations from experimental, historical datasets. We find that, while hard constraints prevent GA and MCMC SR from searching, soft constraints can lead to improved performance both in terms of search effectiveness and model meaningfulness, with computational costs increasing by about an order-of-magnitude. If the constraints do not correlate well with the dataset or expected models, they can hinder the search of expressions. We find Bayesian SR is better these constraints (as the Bayesian prior) than by modifying the fitness function in the GA

• The paper introduces thermodynamic constraints into symbolic regression, ensuring models align with both data and theoretical principles.
• The paper shows that Bayesian symbolic regression integrates these constraints more effectively than genetic algorithms, despite increased computational demands.
• The paper demonstrates that incorporating domain knowledge bridges empirical data with scientific theory, enhancing model interpretability in scientific applications.

Incorporating Background Knowledge in Symbolic Regression using a Computer Algebra System

The paper "Incorporating Background Knowledge in Symbolic Regression using a Computer Algebra System" investigates the addition of background knowledge, particularly through thermodynamic constraints, into symbolic regression (SR) frameworks to generate expressions that possess both data consistency and theoretical relevance. This paper applies SR to rediscover adsorption equations from historical datasets, utilizing both genetic algorithm-based SR (PySR) and Bayesian SR systems. The incorporation of these constraints is evaluated in terms of its impact on performance and computational efficiency.

Overview of Symbolic Regression Application

Symbolic Regression generates mathematical models optimized for data fitting by balancing complexity and accuracy. Unlike black-box machine learning models, SR reveals interpretable expressions, facilitating scientific understanding and extrapolation over extended domains from small datasets. The historical applications of SR cover diverse scientific areas, yet it often disregards theoretical insights by focusing on empirical data alone. The paper posits that integrating background mathematical constraints maintains the relevance of derived expressions within specific scientific fields.

Figure 1: All mutations (except for random tree generation and simplification) in PySR in succession (read from left to right, top to bottom). Changes from each previous expression tree are shown in orange.

Adopting Thermodynamic Constraints in SR

The paper introduces constraints for improving model meaningfulness, focusing primarily on adsorption. These constraints ensure appropriate behavior, such as zero loading at zero pressure and non-decreasing loading with pressure increment. This section discusses how both genetic and Bayesian SR approaches were modified to incorporate these checks. The penalty-based "soft" constraint implementation is employed, allowing for model re-ranking rather than immediate rejection upon constraint failure.

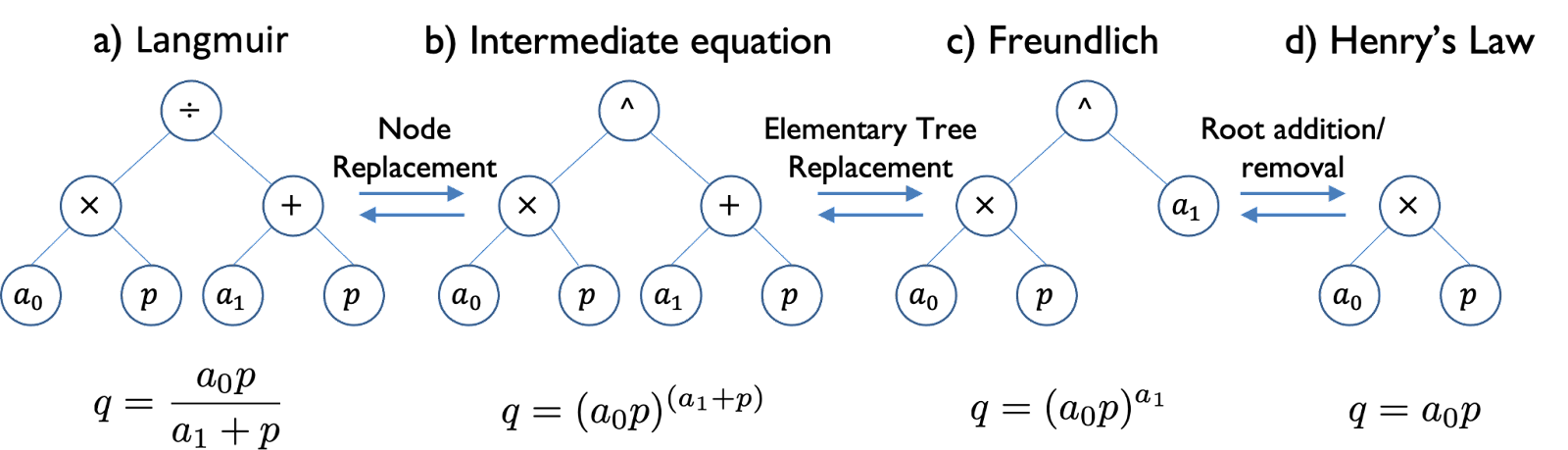
Figure 2: Illustrating the moves available to the BMS algorithm, as applied to adsorption equations. In contrast to the mutations available in PySR, these transformations satisfy detailed balance.

Evaluation and Results

The paper's experimental evaluation involves assessing four adsorption datasets. The findings indicate that Bayesian SR demonstrates better integration of constraints compared to genetic algorithms, with the prior accurately influencing search outcomes. Bayesian approaches consistently deliver highly relevant models; however, genetic algorithms frequently suffer from being trapped in non-thermodynamic expression basins.

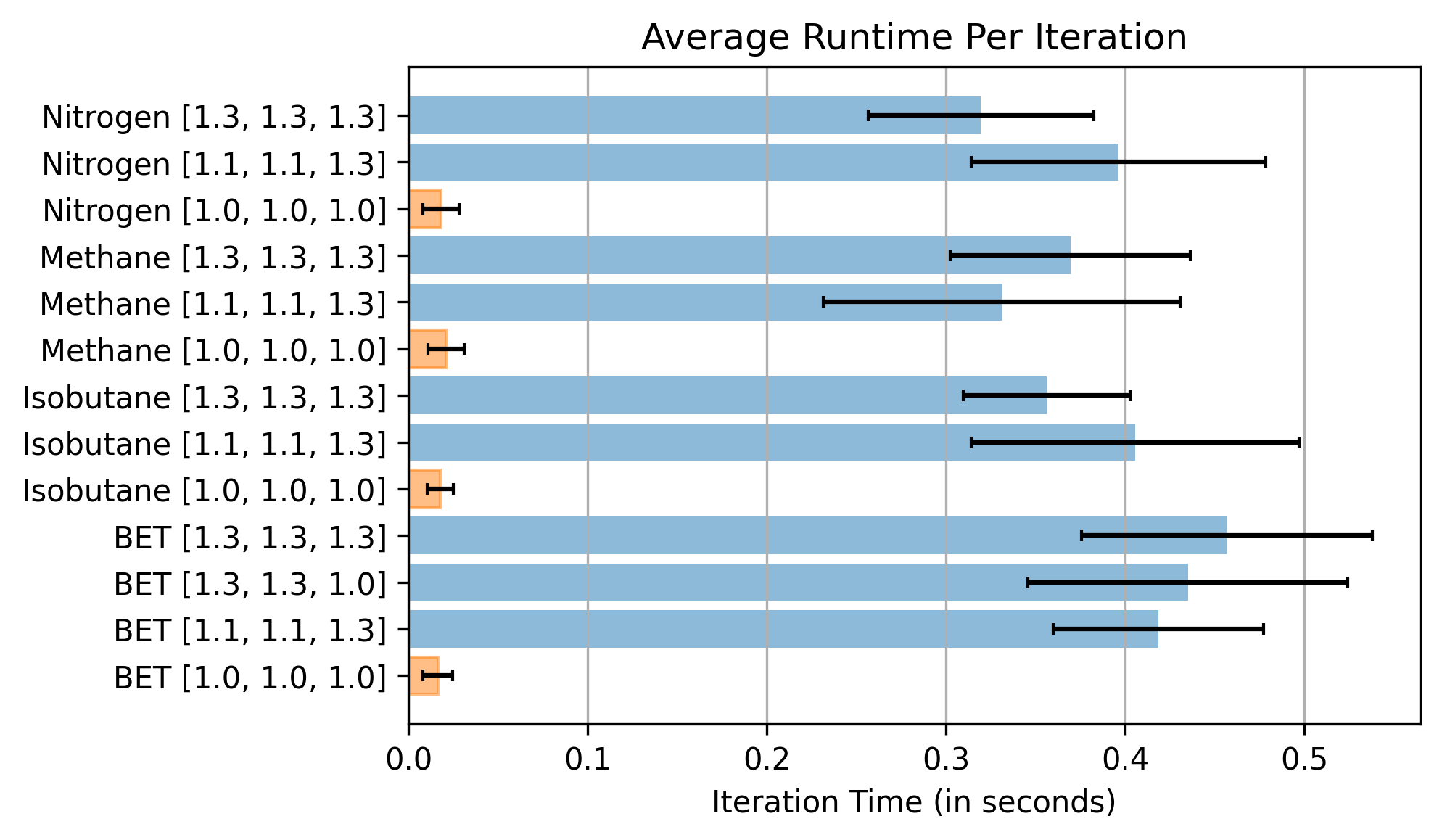
Figure 3: Average runtimes across all datasets and combinations of thermodynamic constraint penalties. Runs with all penalties set to 1.0 are highlighted in orange. Standard deviation is shown by error bars at the top of each bar.

The key results reveal that suitable constraints guide model searches more effectively, but computational costs rise approximately tenfold due to symbolic checks. PySR has particular difficulties with systematic constraint satisfaction due to its less nuanced penalty integration when contrasted with Bayesian methods.

Implications and Future Directions

This research exemplifies the potency of integrating domain knowledge into machine learning workflows, notably within the SR landscape. By intelligently weighting theoretical constraints, SR processes can bridge the gap between empirical and theoretical investigation, advancing model consistency and applicability. Nevertheless, selecting appropriate constraints remains challenging; improper specification impedes search efficacy.

Future explorations could expand on contextualizing background knowledge for broader application domains, refining constraint formulations, and examining alternatives to symbolic check complexities, potentially enabling more viable real-world applications.

Conclusion

The inclusion of thermodynamic constraints effectively contextualizes the symbolic regression process, improving model fidelity to physical theories. While computational demands intensify, these enhancements substantiate SR's value proposition as a blend of data accuracy and theoretical integrity. Bayesian SR emerges as a more coherent platform for constraint integration. This paper's methodologies presage broader adaptability of SR in complex scientific modeling scenarios.