Proximal Learning With Opponent-Learning Awareness (2210.10125v1)

Abstract: Learning With Opponent-Learning Awareness (LOLA) (Foerster et al. [2018a]) is a multi-agent reinforcement learning algorithm that typically learns reciprocity-based cooperation in partially competitive environments. However, LOLA often fails to learn such behaviour on more complex policy spaces parameterized by neural networks, partly because the update rule is sensitive to the policy parameterization. This problem is especially pronounced in the opponent modeling setting, where the opponent's policy is unknown and must be inferred from observations; in such settings, LOLA is ill-specified because behaviorally equivalent opponent policies can result in non-equivalent updates. To address this shortcoming, we reinterpret LOLA as approximating a proximal operator, and then derive a new algorithm, proximal LOLA (POLA), which uses the proximal formulation directly. Unlike LOLA, the POLA updates are parameterization invariant, in the sense that when the proximal objective has a unique optimum, behaviorally equivalent policies result in behaviorally equivalent updates. We then present practical approximations to the ideal POLA update, which we evaluate in several partially competitive environments with function approximation and opponent modeling. This empirically demonstrates that POLA achieves reciprocity-based cooperation more reliably than LOLA.

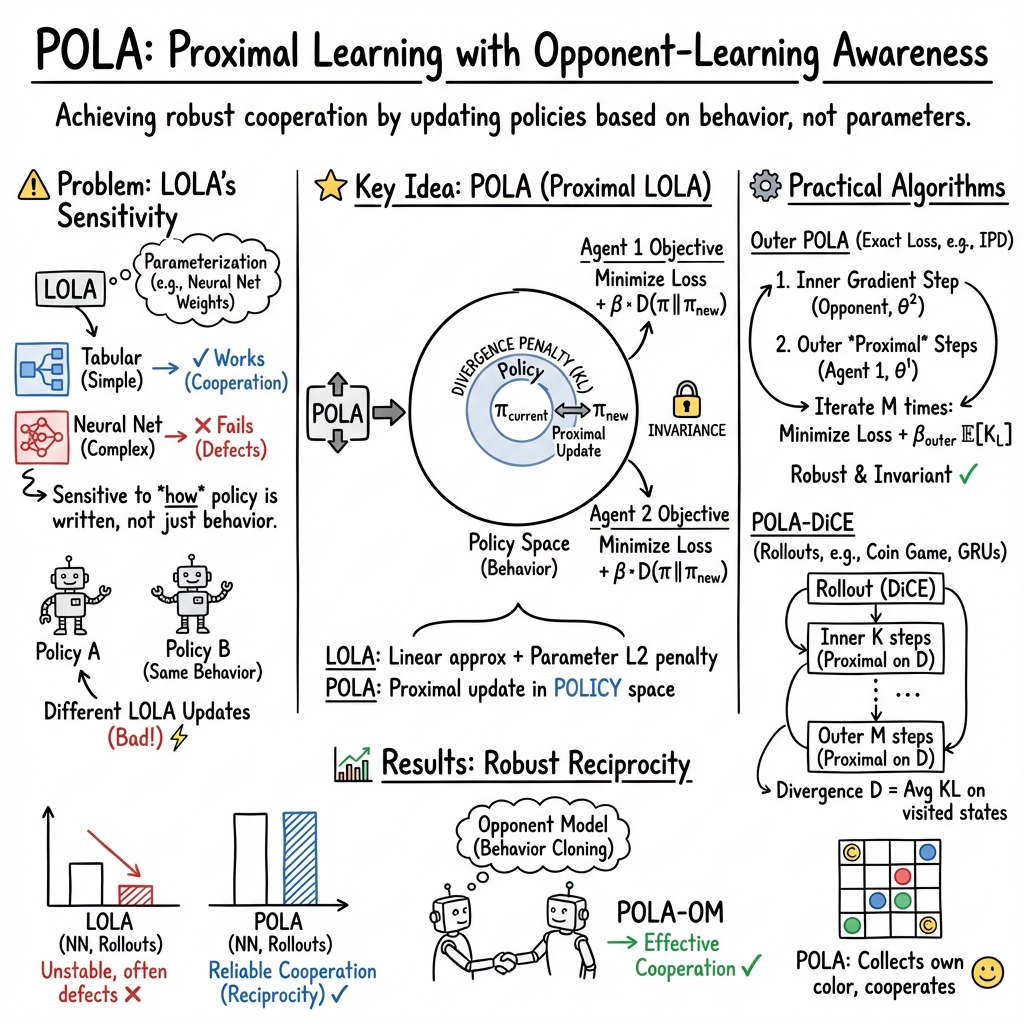
• The paper introduces POLA as a proximal operator reinterpretation of LOLA, achieving parameterization invariance for more reliable reciprocity-based cooperation.
• It leverages outer POLA and POLA-DiCE approximations to provide tractable, first-order updates with unbiased gradient estimation in high-dimensional settings.
• Experiments in iterated prisoner's dilemma and coin games demonstrate POLA’s superior performance and scalability compared to the original LOLA algorithm.

Proximal Learning With Opponent-Learning Awareness

Introduction

The paper "Proximal Learning With Opponent-Learning Awareness" introduces Proximal Learning with Opponent-Learning Awareness (POLA), a novel algorithmic framework designed to address limitations of the Learning With Opponent-Learning Awareness (LOLA) algorithm in multi-agent reinforcement learning (MARL) settings. While LOLA is known to facilitate cooperation in simple social dilemmas, it struggles with neural network-parameterized policies due to sensitivity to policy parameterization. POLA addresses this by reinterpreting LOLA as an approximation of a proximal operator, thus achieving parameterization invariance and improving reliability in learning reciprocity-based cooperation.

Theoretical Developments

At its core, POLA is developed by framing LOLA within proximal algorithms, which are gradient-based optimization techniques renowned for their robustness to parameterization changes. The paper derives POLA updates using proximal formulations that incorporate penalty terms to maintain proximity in the policy space, thus ensuring that behaviorally equivalent policies result in behaviorally equivalent updates. This formulation is particularly advantageous in opponent modeling scenarios where the opponent's policy is not directly observable and must be inferred from interactions.

Practical Approximations of POLA

Given the impracticality of exact POLA updates, the paper presents tractable algorithms: outer POLA and POLA-DiCE. Outer POLA simplifies the original formulation by employing first-order approximations for computational feasibility. POLA-DiCE further adapts these techniques to environments requiring policy gradient methods with rollouts, leveraging DiCE for unbiased gradient estimation in high-dimensional spaces.

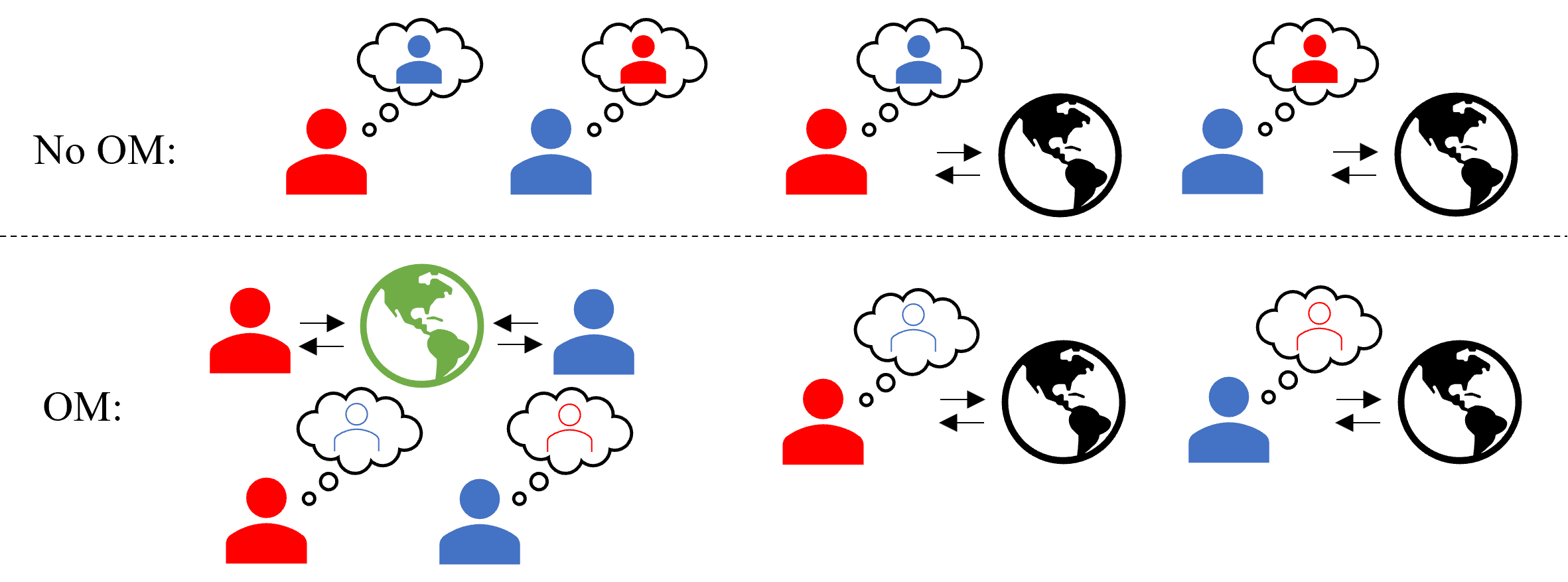
Figure 1: Illustration of the training process at each time step for LOLA-DiCE and POLA-DiCE.

Experimental Analysis

The paper rigorously evaluates POLA in various MARL scenarios, including the iterated prisoner's dilemma (IPD) and the coin game. These experiments highlight POLA's superior performance relative to LOLA in achieving reciprocity-based cooperation across different parameterizations, demonstrating its robustness and scalability in function approximation contexts.

1. One-Step Memory IPD: POLA consistently finds tit-for-tat (TFT) strategies with both tabular and neural network policies, unlike LOLA which fails when policy parameterizations vary significantly.
2. Full Action History IPD: Utilizing GRUs for parameterization, POLA-DiCE agents show a high probability of mutual cooperation while defecting against non-cooperative opponents, maintaining robustness even with opponent modeling.

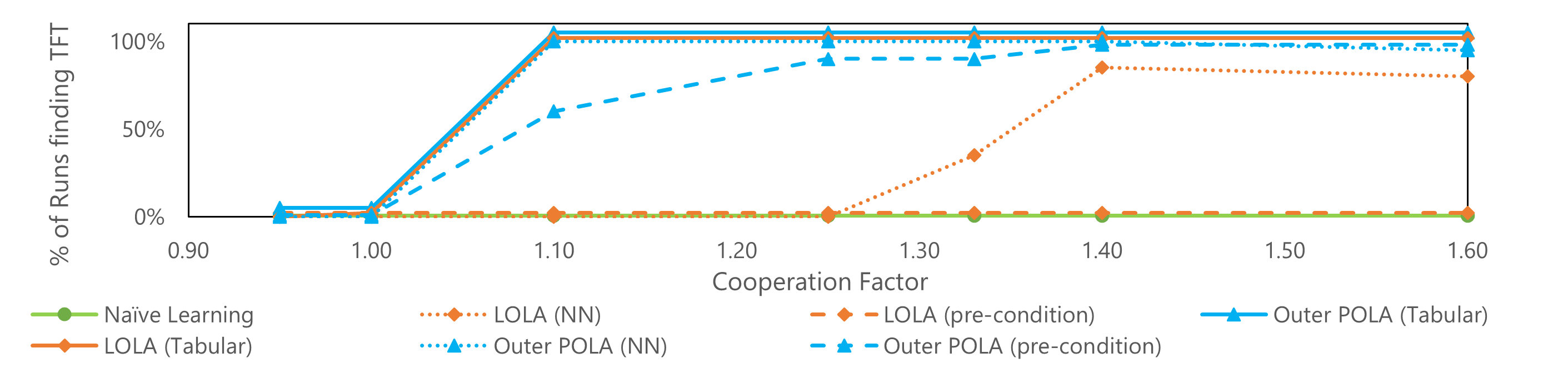
   Figure 2: Comparison of LOLA and outer POLA in the one-step memory IPD.

3. Coin Game: In a high-dimensional observation setting, POLA-DiCE significantly outperforms LOLA-DiCE, achieving near-optimal levels of cooperation while using opponent modeling effectively.

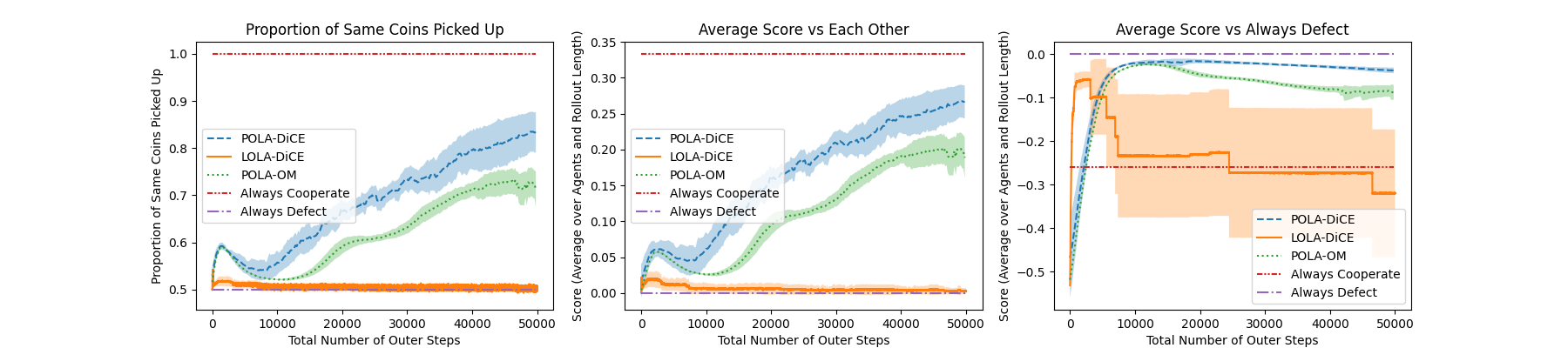
   Figure 3: Comparison of LOLA-DiCE and POLA-DiCE on the coin game.

Implications and Future Work

POLA's invariance to policy parameterization opens new avenues for deploying opponent shaping algorithms in more complex MARL environments. Future research could explore extensions to three or more agents, performance in larger-scale cooperative scenarios, and adaptations that enhance sample efficiency.

Conclusion

The introduction of POLA represents a significant step towards robust, parameterization-invariant cooperative learning in MARL. By addressing the limitations inherent in LOLA, POLA sets the stage for more reliable and scalable solutions in environments demanding intricate strategic interactions among autonomous agents.