Collision Avoidance for Dynamic Obstacles with Uncertain Predictions using Model Predictive Control (2208.03529v1)

Abstract: We propose a Model Predictive Control (MPC) for collision avoidance between an autonomous agent and dynamic obstacles with uncertain predictions. The collision avoidance constraints are imposed by enforcing positive distance between convex sets representing the agent and the obstacles, and tractably reformulating them using Lagrange duality. This approach allows for smooth collision avoidance constraints even for polytopes, which otherwise require mixed-integer or non-smooth constraints. We consider three widely used descriptions of the uncertain obstacle position: 1) Arbitrary distribution with polytopic support, 2) Gaussian distributions and 3) Arbitrary distribution with first two moments known. For each case we obtain deterministic reformulations of the collision avoidance constraints. The proposed MPC formulation optimizes over feedback policies to reduce conservatism in satisfying the collision avoidance constraints. The proposed approach is validated using simulations of traffic intersections in CARLA.

• The paper introduces a novel MPC formulation to ensure collision avoidance in environments with dynamic obstacles and uncertain predictions.
• It reformulates stochastic collision constraints into deterministic ones using Lagrange duality for improved computational efficiency.
• Simulation results across basic tests and CARLA scenarios validate the framework’s effectiveness in achieving safe, collision-free trajectories.

Collision Avoidance for Dynamic Obstacles with Uncertain Predictions using Model Predictive Control

This essay explores the content of the paper titled "Collision Avoidance for Dynamic Obstacles with Uncertain Predictions using Model Predictive Control" (2208.03529). The research introduces a novel application of Model Predictive Control (MPC) to address collision avoidance challenges faced by autonomous agents in environments with dynamic obstacles and uncertain predictions.

Problem Formulation

The core contribution of this paper is the development of MPC formulations for collision avoidance in the presence of dynamic and uncertain environments. The framework is structured around the following key elements:

Dynamics and Geometry

The controlled agent is modeled using a linear time-varying discrete-time system, characterized by state, input, and process noise variables:

$$x_{t+1} = A_tx_t + B_tu_t + E_tw_t, \quad p_t = Cx_t + c_t$$

The obstacles are similarly modeled with affine time-varying dynamics:

$$o^i_{t+1} = T_t^io_{t}^i + q^i_t + F^i_{t}n^i_{t}, \quad p^i_{t} = Co^i_{t}$$

Uncertainty Description

The process noise is described under three different formulations:

1. Arbitrary Distribution with Polytopic Support (D1): The noise takes values from a convex, bounded set.
2. Gaussian Distribution (D2): The noise follows a Gaussian distribution with known variance.
3. Known Moments (D3): The noise distribution is arbitrary but specified by its first two moments.

Model Predictive Control Formulation

MPC is utilized to compute feedback control policies that ensure collision avoidance with dynamically moving obstacles. The policies are parameterized and allow reactions to different trajectory realizations. The paper constructs a deterministic reformulation of collision constraints, optimizing over these reformulated constraints to improve computational efficiency and reliability.

Collision Avoidance Reformulation

By leveraging Lagrange duality, the paper transforms the problem of avoiding collisions into a convex feasibility problem. This approach employs dual variables to ensure non-intersecting trajectories, which is crucial for computational tractability.

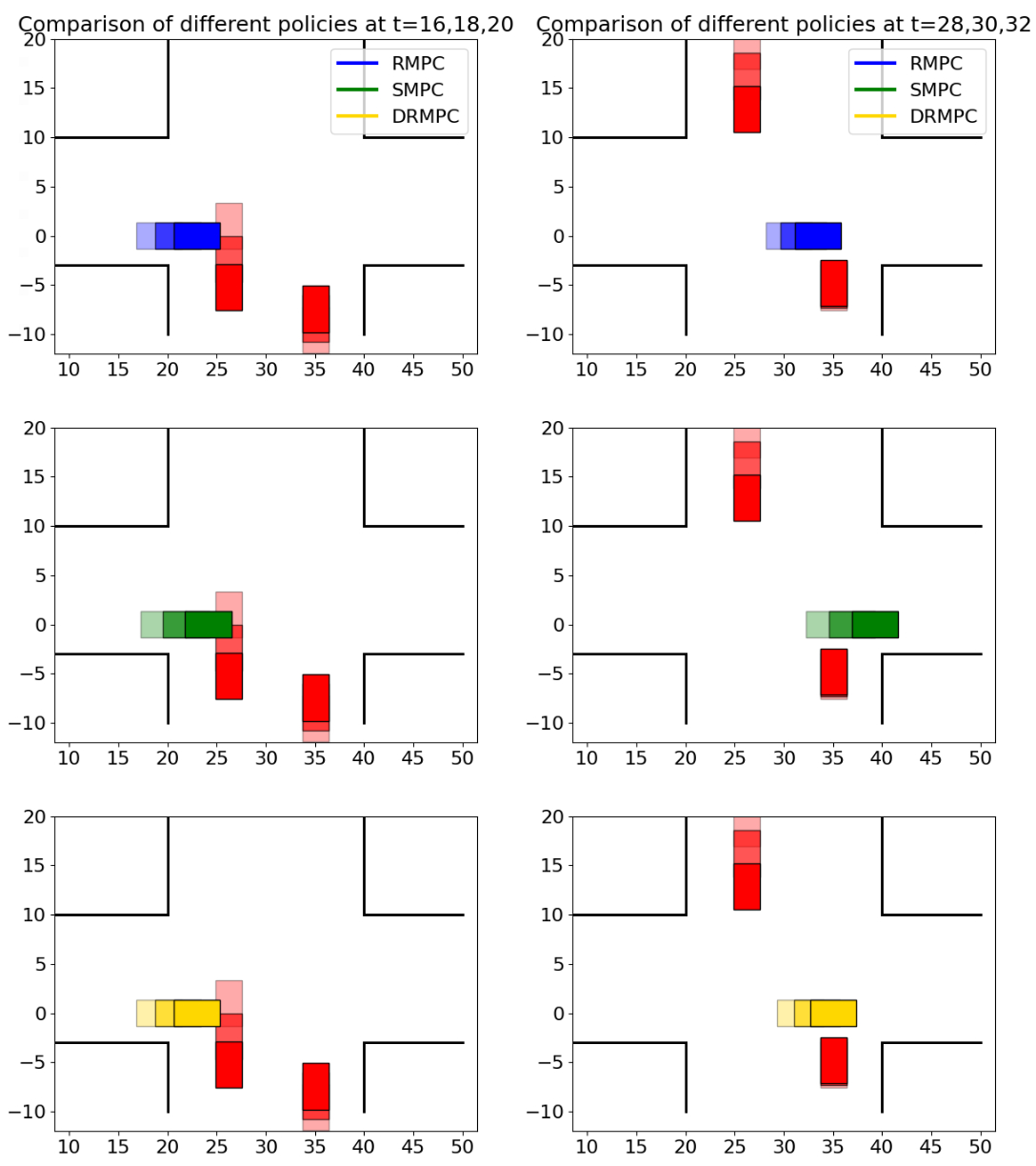
Figure 1: Snapshots of agents with RMPC, SMPC, and DRMPC for specific run parameters, indicating response to obstacle uncertainty.

Deterministic Constraint Reformulation

For practical applications, the paper provides deterministic reformulations of the stochastic constraints based on the description of uncertainty:

1. Robust Formulation for D1: Tightened constraints ensure feasibility against worst-case disturbances.
2. Chance Constraints for D2: Constraints are satisfied with a user-defined probability, providing a balance between robustness and efficiency.
3. Distributionally Robust Constraints for D3: These constraints are designed to hold under all distributions consistent with the known moments.

Simulation Results

The framework was validated through simulations in both basic and complex traffic scenarios. In a longitudinal control setting, different MPC formulations (RMPC, SMPC, DRMPC) were compared, showing trade-offs between conservatism, computational demand, and efficacy in achieving collision-free trajectories.

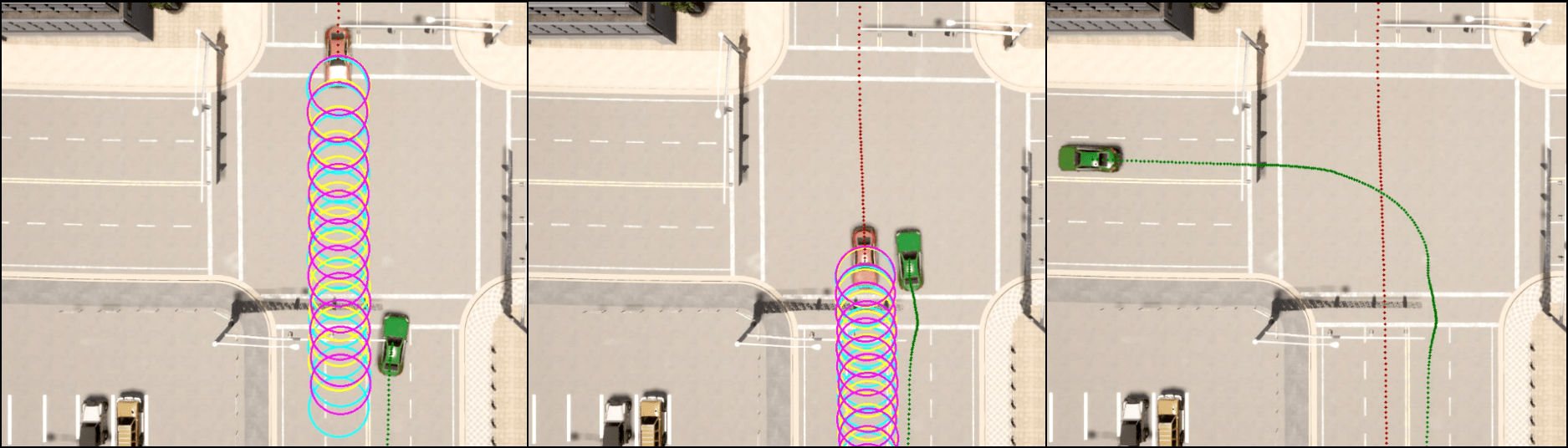
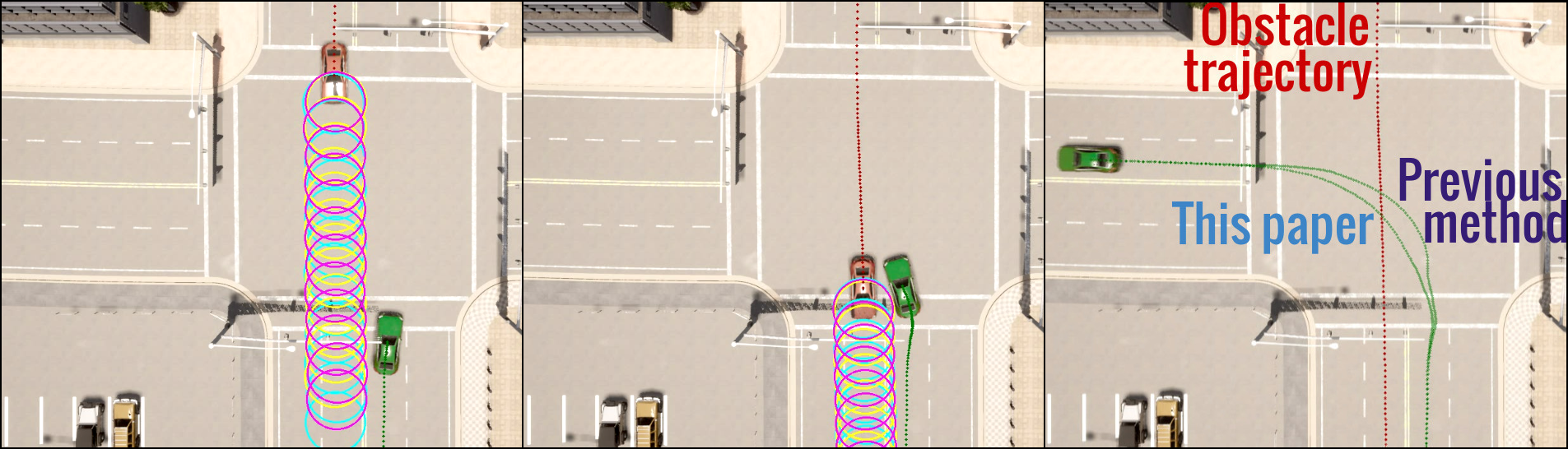
Figure 2: SMPC from referenced work.

CARLA Simulation

Simulations in the CARLA autonomous driving simulator demonstrated the effectiveness of the proposed planner in urban intersections with dynamic obstacles, outperforming conventional methods in terms of tighter and safer maneuvers.

Conclusion

The research successfully presents a practical MPC-based collision avoidance solution tailored for dynamic obstacles with uncertain predictions. The approach combines theoretical innovations with simulations to verify performance improvements. Future work may focus on refining the dual reformulation and expanding it to other types of vehicular and robotic applications.