TabPFN: A Transformer That Solves Small Tabular Classification Problems in a Second (2207.01848v6)

Abstract: We present TabPFN, a trained Transformer that can do supervised classification for small tabular datasets in less than a second, needs no hyperparameter tuning and is competitive with state-of-the-art classification methods. TabPFN performs in-context learning (ICL), it learns to make predictions using sequences of labeled examples (x, f(x)) given in the input, without requiring further parameter updates. TabPFN is fully entailed in the weights of our network, which accepts training and test samples as a set-valued input and yields predictions for the entire test set in a single forward pass. TabPFN is a Prior-Data Fitted Network (PFN) and is trained offline once, to approximate Bayesian inference on synthetic datasets drawn from our prior. This prior incorporates ideas from causal reasoning: It entails a large space of structural causal models with a preference for simple structures. On the 18 datasets in the OpenML-CC18 suite that contain up to 1 000 training data points, up to 100 purely numerical features without missing values, and up to 10 classes, we show that our method clearly outperforms boosted trees and performs on par with complex state-of-the-art AutoML systems with up to 230$\times$ speedup. This increases to a 5 700$\times$ speedup when using a GPU. We also validate these results on an additional 67 small numerical datasets from OpenML. We provide all our code, the trained TabPFN, an interactive browser demo and a Colab notebook at https://github.com/automl/TabPFN.

• The paper introduces TabPFN, a Transformer-based model that performs small tabular classification in under one second without parameter tuning.
• It integrates Bayesian neural networks and structural causal models into a synthetic prior, enabling fast approximation of the Bayesian posterior predictive distribution.
• Empirical results show that TabPFN achieves competitive or superior ROC-AUC to tuned SOTA methods on numerical datasets, with a dramatic speedup in inference time.

TabPFN: Training a Transformer for Small Tabular Classification via Prior-Data Fitted Networks

Introduction and Motivation

The paper introduces TabPFN, a Prior-Data Fitted Network (PFN) based on a Transformer architecture, trained to perform supervised classification for small-scale tabular datasets in under one second—with no parameter tuning—while achieving accuracy competitive with state-of-the-art (SOTA) baselines. In contrast to standard practice, where a new model is fitted from scratch for each novel dataset, TabPFN executes a forward pass on a pre-trained Transformer to deliver immediate predictions. The key innovation is the use of a synthetic data prior incorporating both Bayesian neural networks (BNNs) and structural causal models (SCMs), imbuing the model with nontrivial inductive biases relevant to real-world tabular regimes.

Prior-Data Fitted Networks and the TabPFN Architecture

TabPFN builds on Prior-Data Fitted Networks [muller-iclr22a], which aim to approximate the Bayesian posterior predictive distribution (PPD) for any expressly defined dataset prior. This is achieved by simulating a large distribution of training tasks (sampled from a prior over data-generating mechanisms) and training a Transformer to directly output $p(y \mid x, D_{train})$ for arbitrary test points and training sets.

The architectural modifications relative to prior PFN work include:

• Specialized attention masking for faster inference.
• Schema-agnostic feature handling via zero-padding, permitting input sets with varying feature dimensionality.
• In-context learning (ICL) ability, where prediction is performed via a single forward pass using a sequence of (x, y) pairs, without updating model parameters at inference time.

Synthetic Prior Design: Integrating Causality and Simplicity

A critical component is the synthetic prior generating the datasets used for pretraining. This prior consists of a mixture of BNNs and SCM-based generators:

• BNN prior: Captures complex, nonlinear predictive relationships (but without explicit structural causality).
• SCM prior: Models causal mechanisms, feature interdependence, and the possibility of features being causes or effects of labels, following the formalism of directed acyclic graphs with stochastic structural equations [pearl_2009].

Both prior types are parameterized with distributions (not point values) over all hyperparameters—including model architectures, noise structures, and edge sparsity—in a fully Bayesian manner, enabling the PPD to integrate over all plausible dataset generation scenarios. Occam's Razor is encoded by increasing the prior probability of simpler SCMs/BNNs (e.g., fewer nodes, sparse graphs).

The prior also incorporates:

• Realistic feature correlation structures through blockwise sampling.
• Varied activation nonlinearities, noise distributions, and input data marginals.
• Extension to multi-class and imbalanced label generation by binning continuous outcomes and randomizing interval-label assignment.
• Robustness to non-numeric data types via randomized categorical feature simulation, although with reduced performance on categorical/missing-datum regimes.

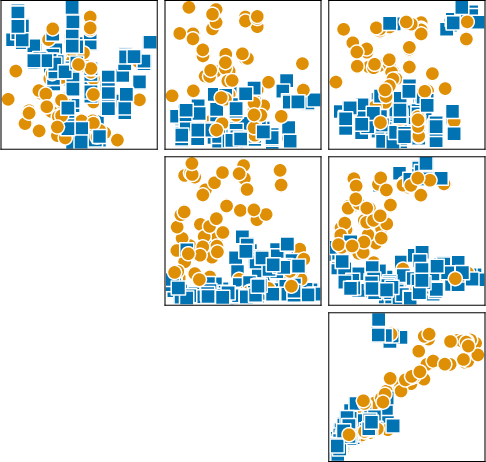
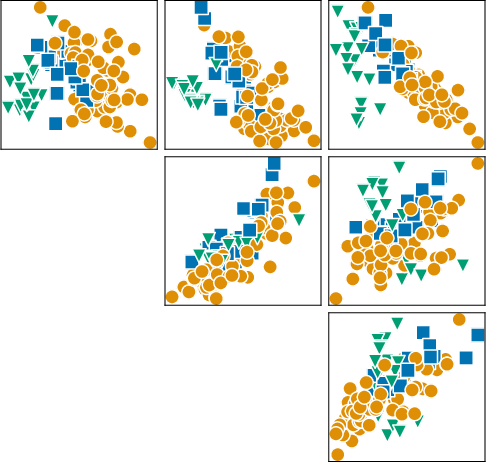
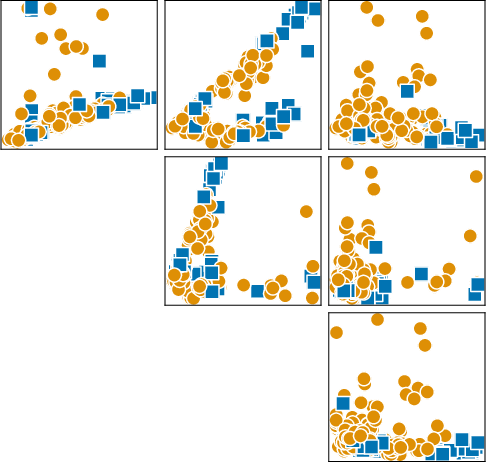
Figure 2: Synthetic datasets sampled from SCM-based and BNN-based priors, capturing realistic label boundaries and feature intercorrelations.

Training and Inference Pipeline

Offline training is performed over millions of synthetic datasets, where TabPFN is optimized to output the class probabilities for held-out samples given a training set, minimizing the cross-entropy error relative to the ground-truth labels. The training procedure generalizes across number of features ($\leq$100), samples ($\leq$1,000), and classes ($\leq$10). Once trained, the network’s parameters are frozen.

Inference on a new (real) dataset concatenates training and test features (and their labels where available); the Transformer produces predictions for all test instances simultaneously. There is no retraining or fine-tuning. Ensembling is achieved by running multiple deterministic or randomized forward passes (e.g., with power-transformed features, permuted feature/class order) and averaging predictions.

Empirical Evaluation

Qualitative Boundary Learning

TabPFN learns smooth and plausible classification boundaries, with confidence (uncertainty) qualitatively matching the density of observed samples. On synthetic and real toy problems, TabPFN closely approximates optimal Bayes boundaries, often showing uncertainty far from training data, as in GPs.

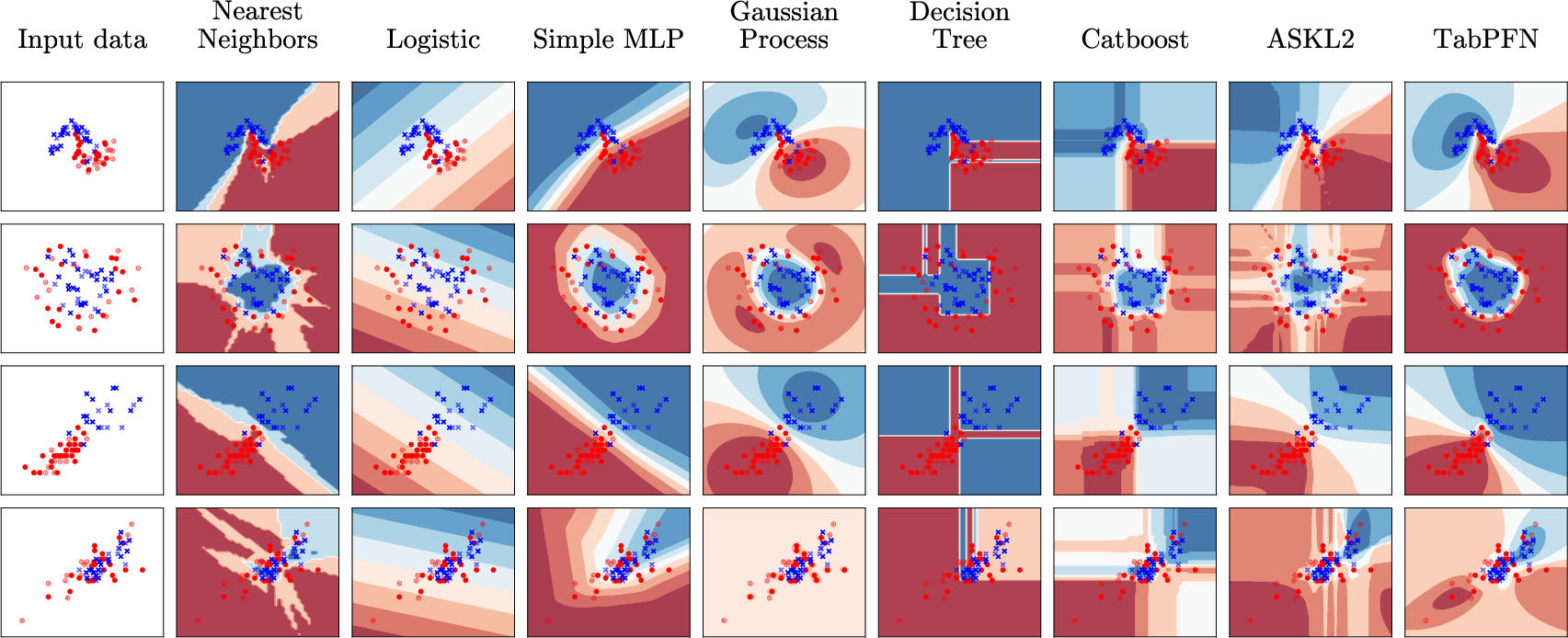
Figure 4: Comparison of decision boundaries on scikit-learn toy datasets, where TabPFN accurately models complex shapes and uncertainty.

Benchmarking Against SOTA Methods

TabPFN is compared to:

• GBDT methods: XGBoost [chen-kdd16a], LightGBM [ke-neurips17a], CatBoost [prokhorenkova-neurips18a]
• Simple baselines: Logistic Regression, KNN
• Automated ML systems: AutoGluon [erickson-arxiv20a], Auto-sklearn 2.0 [feurer-arxiv20v2]
• Deep tabular methods: SAINT [somepalli2021saint], Regularization Cocktails [regcocktail]

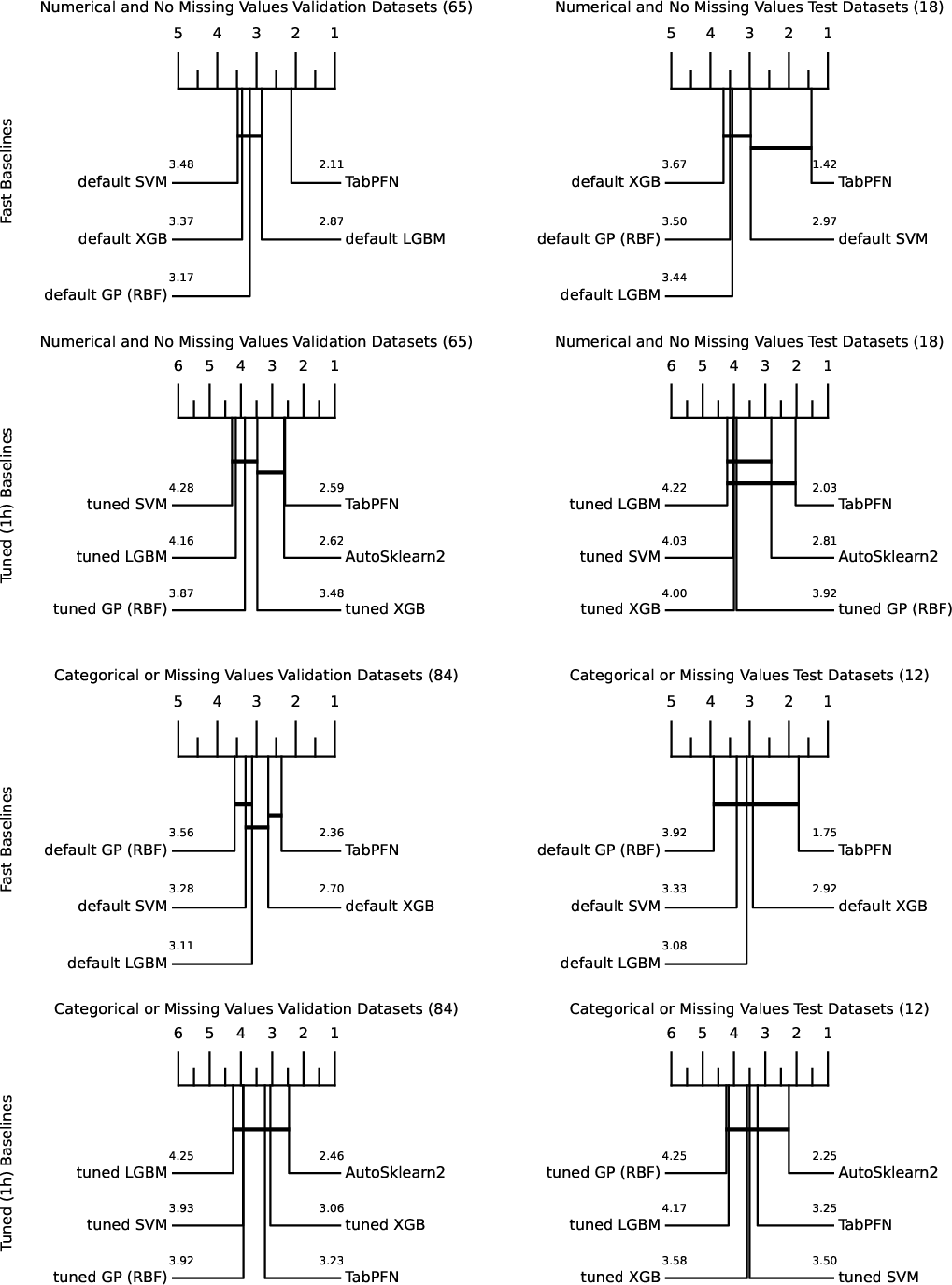
Key findings on 18 OpenML-CC18 numerical datasets (≤1,000 training points, ≤100 features, ≤10 classes, no missing values):

• TabPFN achieves competitive or superior ROC-AUC to tuned GBDTs and AutoML systems, with >200x speedup on CPU and >5,000x on GPU when using ensemble predictions.
• The process requires $<1$s per dataset (including data preprocessing), vastly outperforming the median inference and tuning times of the baselines, which require several minutes to hours.
• On purely numerical datasets, TabPFN statistically significantly outperforms all compared methods in the "fast" setting ($<$30s total runtime).

  Figure 1: Critical difference plots reveal that, on purely numerical datasets, TabPFN achieves statistically significant superiority over other methods under tight runtime constraints.

Inductive Biases and Generalization

• TabPFN exhibits strong inductive bias towards smooth, simple decision boundaries (favored by its SCM prior), differing from the piecewise axis-aligned boundaries favored by trees.
• Out-of-sample generalization: TabPFN is able to extrapolate to larger datasets (up to 5,000 samples) than seen in pretraining, albeit with some degradation.
• Distinct error profiles: Per-dataset performance correlations between TabPFN and GBDTs/AutoML are low (Figure 6), suggesting that TabPFN’s errors are largely uncorrelated and thus improve ensemble diversity.

  Figure 3: Spearman correlation matrix confirms that TabPFN's performance is complementary to GBDT and AutoML methods.

• Failure modes: Degradation is observed in datasets with many categorical features, missing values, or a high proportion of uninformative features—owing to prior limitations and representation constraints. For instance, on highly categorical datasets like ‘sensory’ or when features are randomized, TabPFN performance lags.

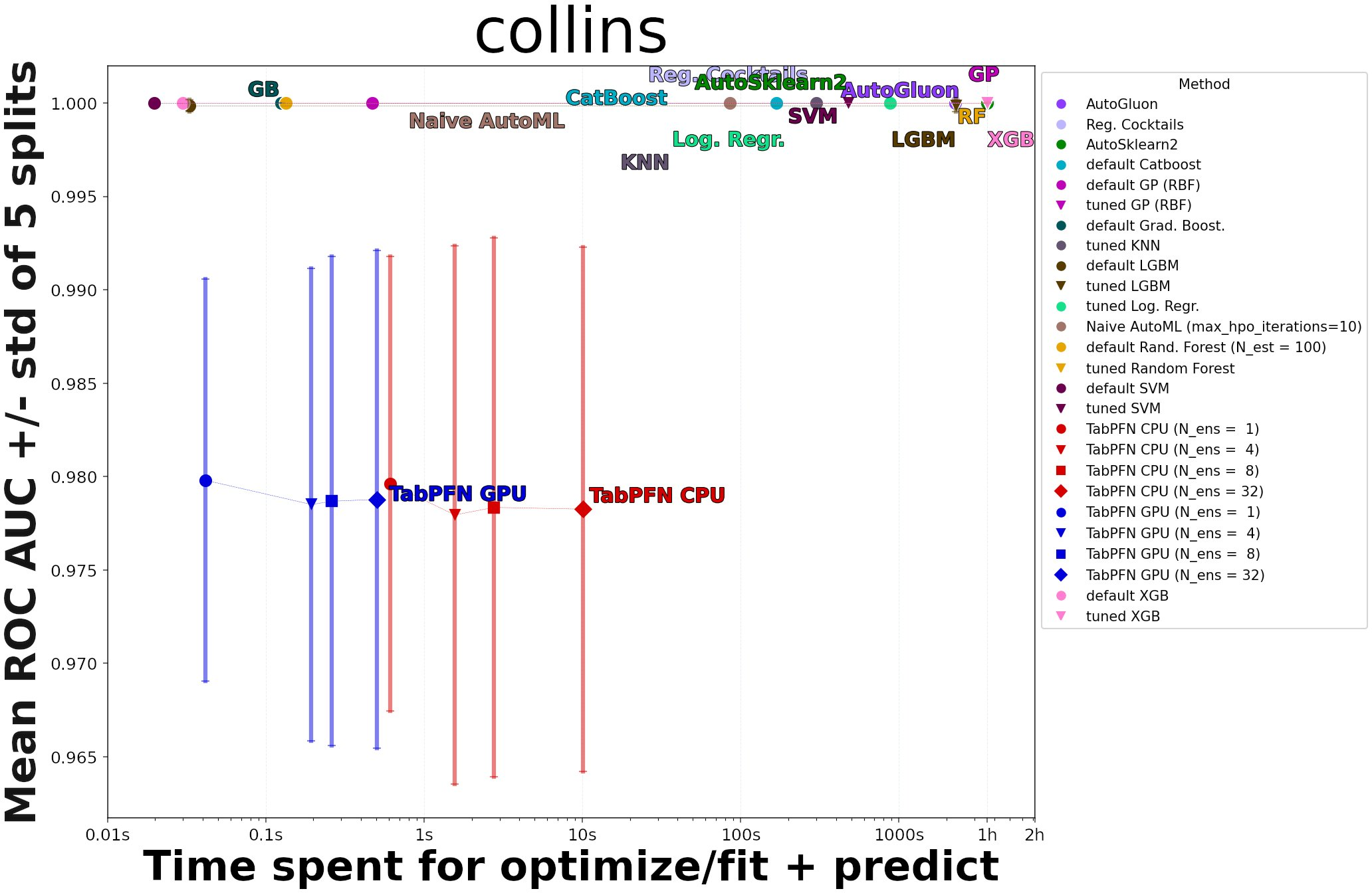
  Figure 8: ROC-AUC performance for the 'collins' dataset—an example where uninformative features confound TabPFN, highlighting prior limitations.

Practical Implications and Theoretical Considerations

TabPFN’s paradigm shifts the computational and resource demands of tabular ML:

• One-time, amortized training cost
• Negligible per-dataset inference—enabling real-time classification, interactive analytics, and dramatically lower environmental and financial costs

This approach suggests that, for small- to medium-sized tabular regimes, significant gains can be made by reconceptualizing model selection/hyperparameter optimization as an offline meta-optimization task, leveraging generative priors tailored to target application domains.

Theoretical implications:

• Empirical Bayes at scale: TabPFN demonstrates a scalable approach to black-box Bayesian prediction approximating the marginalization over an entire space of plausible mechanisms, without explicit inference at prediction time.
• Causality-motivated generalization: The integration of SCMs into the data prior introduces causal inductive bias, which can benefit robustness to distribution shift and overfitting on small data.
• Automatic hyperparameter marginalization: The Bayesian treatment of model structure/parameters removes the need for manual or meta-learned hyperparameter search for each new task.

Limitations and Future Directions

• Scaling: The current quadratic scaling of Transformer self-attention limits TabPFN to datasets of about 1,000 examples, due to memory and computational cost. Several efficient Transformer architectures (Longformer, BigBird, Nyströmformer) are potential avenues for extending to larger datasets [zaheer2020big, beltagy2020longformer, xiong2021nystromformer].
• Categorical/missing data handling: The model underperforms on datasets with predominantly categorical features or missing values, warranting richer priors and possibly specialized tokenization schemes.
• Uninformative feature robustness: Integration of more realistic priors over feature relevance may reduce sensitivity to irrelevant features.
• Extension to regression, active learning, and trustworthy AI: Future work can target regression, improved handling of dataset peculiarities, robust ensembling, and deeper exploration of applications in exploratory data analytics and trustworthy AI dimensions (e.g., OOD generalization, fairness, explainability, adversarial robustness).

Conclusion

TabPFN exemplifies a shift in tabular ML from per-dataset model fitting and selection to the meta-level: leveraging a single, offline-trained, generative-prior-informed Transformer that delivers immediate, state-of-the-art predictions for unseen tabular datasets. For small, numerical tabular tasks, this reduces typical wall times for SOTA ML from hours to subseconds, while matching or outperforming well-tuned baselines. Its Bayesian, causality-sensitive inductive bias affords improved generalization and diverse error profiles, making it suitable for ensembling. The limitations with non-numerical data and quadratic complexity remain, but the work sets a precedent for the integration of prior-informed, meta-learned, in-context predictors in tabular ML, with broad potential for extensions to other settings and as a complement to existing AutoML systems.