SGD and Weight Decay Secretly Minimize the Rank of Your Neural Network (2206.05794v7)

Abstract: We investigate the inherent bias of Stochastic Gradient Descent (SGD) toward learning low-rank weight matrices during the training of deep neural networks. Our results demonstrate that training with mini-batch SGD and weight decay induces a bias toward rank minimization in the weight matrices. Specifically, we show both theoretically and empirically that this bias becomes more pronounced with smaller batch sizes, higher learning rates, or stronger weight decay. Additionally, we predict and empirically confirm that weight decay is essential for this bias to occur. Unlike previous literature, our analysis does not rely on assumptions about the data, convergence, or optimality of the weight matrices, making it applicable to a wide range of neural network architectures of any width or depth. Finally, we empirically explore the connection between this bias and generalization, finding that it has a marginal effect on the test performance.

• The paper's main contribution is showing that SGD with weight decay effectively minimizes the rank of weight matrices through controlled update dynamics.
• The theoretical framework reveals that weight matrices in both convolutional and fully connected layers converge to bounded rank configurations under small batch conditions.
• Empirical analyses on architectures like ResNet and VGG confirm that a lower rank bias correlates with slightly improved test performance while offering insights into model generalization.

SGD and Weight Decay Secretly Minimize the Rank of Your Neural Network

Introduction

The paper explores how Stochastic Gradient Descent (SGD) combined with weight decay implicitly biases neural networks towards learning weight matrices of low rank. This property is examined across various architectures, without assumptions regarding data or convergence, distinguishing it from existing literature. The paper provides theoretical predictions and empirical validations that smaller batches, higher learning rates, and increased weight decay accentuate this bias.

Theoretical Framework

The analysis begins by demonstrating that the rank of gradients with respect to any weight matrix is upper-bounded by the number of patches in a convolutional layer or by 1 for fully connected layers. This implies that SGD produces updates of bounded rank, particularly when using small batch sizes. This foundational observation is further extended to show that weight matrices evolve toward having bounded rank as training progresses under mini-batch SGD with weight decay.

This behavior is explained via Lemma 3.2, stating that $W^{l}_{T}$ can be seen as a combination of the original matrix and a sum of gradients, each with bounded rank. Over iterations, this sum leads to a negligible distance from a low-rank configuration, formalized as follows:

Theorem 3.4: For large $T$, the normalized weight matrices $\frac{W^{l}_T}{\|W^{l}_T\|}$ approximate a matrix of rank $\leq \frac{m_lB\log(2/\epsilon)}{2\mu\lambda}$, highlighting the central thesis that SGD implicitly enforces low rank.

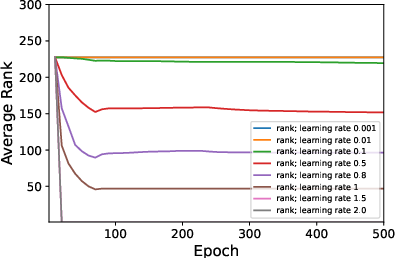
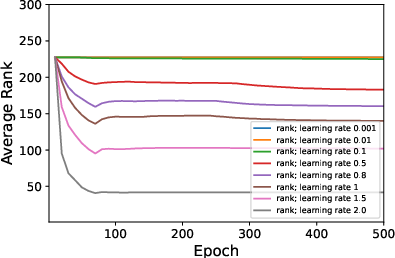
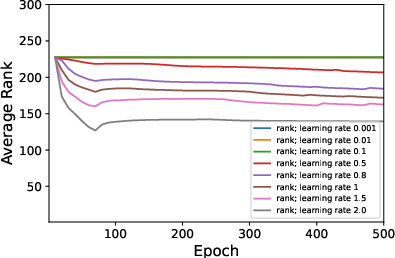
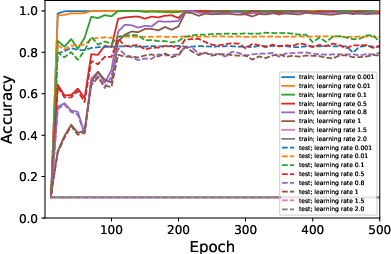
Figure 1: Average ranks and accuracy rates of ResNet-18 trained on CIFAR10 when varying $\mu$.

Empirical Analysis

To validate theoretical predictions, comprehensive experiments were conducted with different architectures like ResNet-18, MLP-BN-10-100, VGG-16, and ViT across datasets including CIFAR10, MNIST, and SVHN.

Key Observations:

• Decreased batch size or increased learning rates and weight decay consistently result in lower rank weight matrices.
• The absence of weight decay significantly reduces or nullifies the observable low-rank bias, even with adjustments to $\mu$ or $B$.
• Surprisingly, despite its minimal impact on generalization, a lower-rank bias correlates with slightly better test performance.

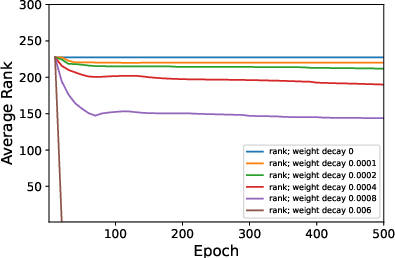
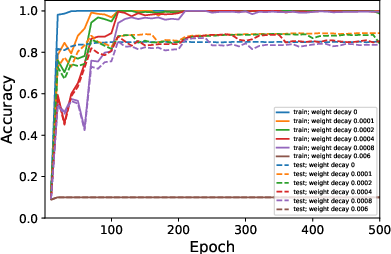
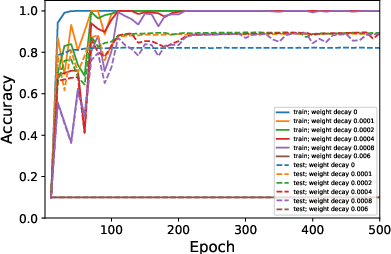
Figure 2: Average ranks and accuracy rates of ResNet-18 trained on CIFAR10 when varying $\lambda$.

Discussion

The paper's implications are significant for understanding the dynamics of modern deep networks. The implicit regularization via SGD, specifically the minimization of rank, provides insights into how models trained this way can effectively generalize. Although low-rank configurations are not singularly responsible for this generalization, they appear to support it. The results suggest that tuning hyperparameters to influence this bias could serve as an additional tuning mechanism to achieve desired model characteristics.

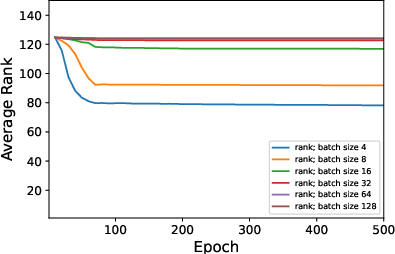
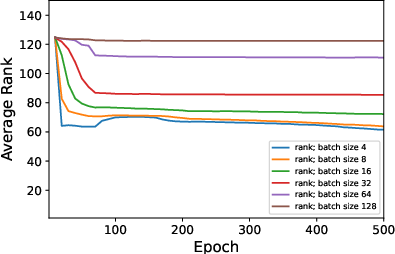
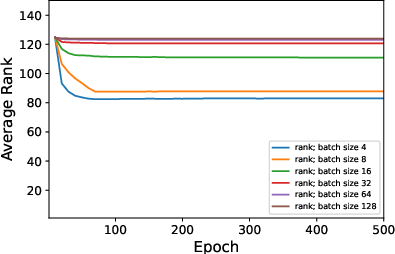
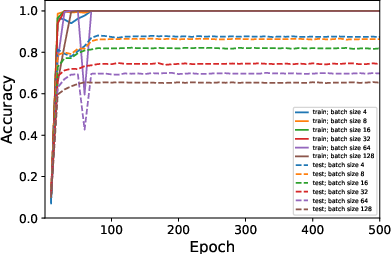
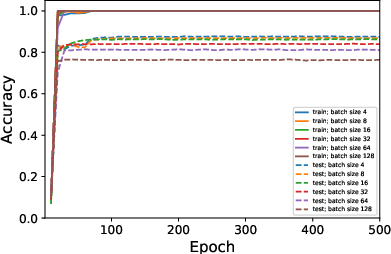
Figure 3: Average rank of Figure 4 trained on CIFAR10 when varying $\epsilon$ in rank approximation.

Future Work Considerations

The paper prompts several avenues for future exploration:

• Extensions of this theory to other forms of SGD-like optimizations or alternative regularization frameworks.
• Studies on the interaction with other forms of implicit bias such as sparsity induction or dropout.
• An exploration into the consequences of low-rank bias on overall network interpretability.

Conclusion

This paper elucidates a subtle yet pervasive bias in neural network training. By demonstrating that SGD implicitly prefers low-rank weight configurations through theoretical and empirical means, it bridges an important gap in understanding the inner workings of deep learning. Although limited in its standalone influence on generalization, this rank minimization bias forms an essential part of the toolkit for characterizing and enhancing model performance.