Recent Advances for Quantum Neural Networks in Generative Learning (2206.03066v1)

Abstract: Quantum computers are next-generation devices that hold promise to perform calculations beyond the reach of classical computers. A leading method towards achieving this goal is through quantum machine learning, especially quantum generative learning. Due to the intrinsic probabilistic nature of quantum mechanics, it is reasonable to postulate that quantum generative learning models (QGLMs) may surpass their classical counterparts. As such, QGLMs are receiving growing attention from the quantum physics and computer science communities, where various QGLMs that can be efficiently implemented on near-term quantum machines with potential computational advantages are proposed. In this paper, we review the current progress of QGLMs from the perspective of machine learning. Particularly, we interpret these QGLMs, covering quantum circuit born machines, quantum generative adversarial networks, quantum Boltzmann machines, and quantum autoencoders, as the quantum extension of classical generative learning models. In this context, we explore their intrinsic relation and their fundamental differences. We further summarize the potential applications of QGLMs in both conventional machine learning tasks and quantum physics. Last, we discuss the challenges and further research directions for QGLMs.

• The paper presents quantum generative learning models (QCBMs, QGANs, QBMs, QAEs) that leverage parameterized quantum circuits for synthetic data generation and state preparation.
• The paper outlines tailored optimization strategies combining classical and quantum techniques to overcome read-in/read-out bottlenecks and nonconvex loss landscapes.
• The study highlights applications in quantum chemistry, finance, and machine learning while emphasizing advancements in noise resilience and scalable quantum computing.

Recent Advances for Quantum Neural Networks in Generative Learning

Introduction

Quantum neural networks, notably implemented via quantum generative learning models (QGLMs), are being strategically positioned as a potential paradigm for delivering computational capabilities beyond classical counterparts due to their inherent probabilistic structure consistent with quantum mechanics. This essay examines the recent advances and application strategies for quantum neural networks in generative learning as elaborated in the document "Recent Advances for Quantum Neural Networks in Generative Learning".

Overview of Quantum Generative Learning Models (QGLMs)

QGLMs, as characterized in the document, serve as quantum enhancements to classical generative models and can be categorized primarily into quantum circuit Born machines (QCBMs), quantum generative adversarial networks (QGANs), quantum Boltzmann machines (QBMs), and quantum autoencoders (QAEs).

• Quantum Circuit Born Machine (QCBM): QCBMs adopt quantum neural networks (QNNs) to form discrete probability distributions effectively and are typically designed using hardware-efficient parameterized quantum circuits. QCBMs are instrumental in tasks like generating synthetic data, learning empirical data distributions in finance, and specific quantum state preparations (e.g., GHZ states).
• Quantum Generative Adversarial Networks (QGANs): QGANs mimic their classical counterparts albeit leveraging the quantum field to theoretically exploit advantages in training adversaries. For instance, QGANs operate via QNNs as generators or discriminators in different configurations, targeting both quantum and classical tasks, as evidenced in domains ranging from financial derivatives to quantum state tomography.
• Quantum Boltzmann Machines (QBMs): QBMs introduce quantum dynamics into the formulation of Boltzmann machines by utilizing quantum transverse Ising models, thereby enabling entropic distribution sampling with potential advantage in large-dimensional problem spaces due to quantum parallelism.
• Quantum Autoencoders (QAEs): QAEs provide data compression and dimensionality reduction directly in the quantum state space, which can delineate efficiency gains in quantum information processing applications, including quantum communication and state reconstruction.

  Figure 1: Key landmarks in the development of QGLMs.

Preliminaries of Quantum Computing Framework

The efficacy of QGLMs builds on the overarching principles of quantum computing, which employs qubits that facilitate superposition and entanglement, operating within quantum circuits composed of quantum gates. Quantum generative models inherit these paradigms by incorporating the principles of variational quantum algorithms to optimize parameterized circuits, where both unitary transformations and state measurements play pivotal roles in model training processes.

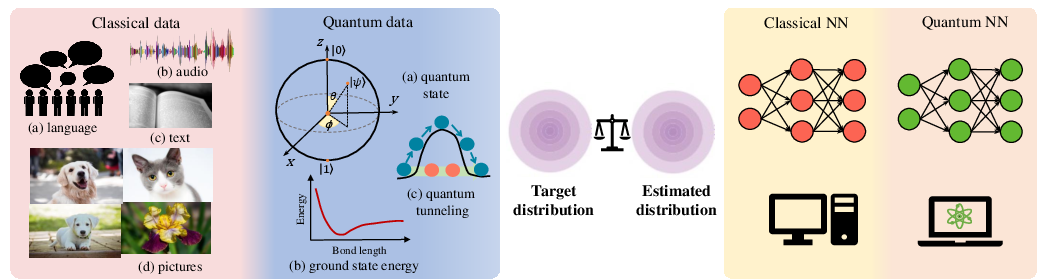
Figure 2: An overview of classical and quantum generative learning models. The left panel illustrates data distributions of interest in both classical and quantum generative learning.

Implementation Challenges and Strategies

1. Read-In and Read-Out Bottleneck: Efficiently encoding classical information into quantum states and extracting quantum information into the classical domain remain formidable. Advances in quantum feature maps and randomized measurements have shown promise in mitigating these issues.
2. Optimizer Synergy: QGLMs require tailored optimization techniques leveraging both classical optimizers (e.g., gradient-free PSO and CMA-ES) and quantum-aware strategies to address non-convex loss landscapes prevalent in quantum settings.
3. Quantum Noise Resilience: Although hardware noise presents challenges, strategies include incorporating error mitigation techniques and exploring adaptive CircuitAnsatz designs to improve noise resilience while maintaining model expressivity.

Potential Applications and Future Directions

QGLMs are gaining traction in applications demanding significant computational depth and circuit expressivity, including:

• Quantum Chemistry: State preparation and Hamiltonian simulation tasks where QGLMs improve efficiency and accuracy.
• Finance: Probabilistic modeling for financial instruments leveraging QGLMs' quantum feature performance.
• Machine Learning Task Parallelism: Enhancing classical algorithms by incorporating quantum speed-ups for clustering, classification, and unsupervised tasks.

Future Work: Development of more robust theoretical frameworks around QGLMs, including their expressivity, learnability, and generalization capabilities, remains crucial. Moreover, task-specific QGLMs architectures that pace the transition from NISQ device regimes to fault-tolerant quantum computations are expected to form new frontiers in scalable quantum learning models.

Conclusion

This investigation into the latest progress in the field of quantum neural networks for generative learning elucidates significant strides towards their practical applicability and theoretical potential. While challenges remain, particularly in scalable implementation and noise resiliency, the potential computational advantages for tackling complex generative tasks position QGLMs as critical tools in the advancing landscape of quantum computing applications.