Deep Learning meets Nonparametric Regression: Are Weight-Decayed DNNs Locally Adaptive? (2204.09664v4)

Abstract: We study the theory of neural network (NN) from the lens of classical nonparametric regression problems with a focus on NN's ability to adaptively estimate functions with heterogeneous smoothness -- a property of functions in Besov or Bounded Variation (BV) classes. Existing work on this problem requires tuning the NN architecture based on the function spaces and sample size. We consider a "Parallel NN" variant of deep ReLU networks and show that the standard $\ell_2$ regularization is equivalent to promoting the $\ell_p$-sparsity ($0<p<1$) in the coefficient vector of an end-to-end learned function bases, i.e., a dictionary. Using this equivalence, we further establish that by tuning only the regularization factor, such parallel NN achieves an estimation error arbitrarily close to the minimax rates for both the Besov and BV classes. Notably, it gets exponentially closer to minimax optimal as the NN gets deeper. Our research sheds new lights on why depth matters and how NNs are more powerful than kernel methods.

• The paper shows that weight decay in deep ReLU networks yields ℓp-sparsity, enabling local adaptivity and minimax-rate estimation for Besov and BV functions.
• The proposed parallel neural network architecture uses ensemble subnetworks to effectively capture heterogeneous smoothness, outperforming traditional kernel methods.
• Empirical experiments and theoretical insights highlight that deeper networks improve adaptive function approximation in complex nonparametric regression settings.

Deep Learning meets Nonparametric Regression: Are Weight-Decayed DNNs Locally Adaptive?

Introduction

The paper investigates the capabilities of deep neural networks (DNNs) within the framework of nonparametric regression, specifically examining their adaptability to functions with heterogeneous smoothness, which are characteristic of Besov or Bounded Variation (BV) classes. Traditional methodologies often tune the architecture of neural networks based on the function spaces and sample sizes, but this work proposes a distinct "Parallel NN" variant of deep ReLU networks. By leveraging standard $\ell_2$ regularization techniques, the authors demonstrate its equivalence in promoting $\ell_p$-sparsity ($0 < p < 1$) and establish that this network can achieve estimation errors near minimax rates for both the Besov and BV classes. Their findings underscore the influential role of network depth in enhancing learning efficacy, suggesting that deeper networks hold significant advantages over shallow counterparts and kernel methods.

Parallel Neural Networks

This paper focuses on a specialized neural network architecture, called the "Parallel Neural Network," which consists of an ensemble of subnetworks. Such architectures are effectively regularized using weight decay, which parallels the sparsity-promoting effect found in adaptive regression methodologies. The ensemble nature allows each subnetwork within the parallel network to specialize, facilitating the model's adaptability across varying function smoothness and complexities.

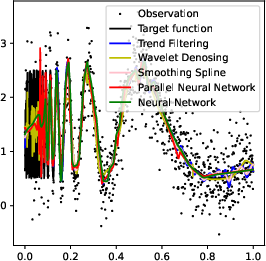
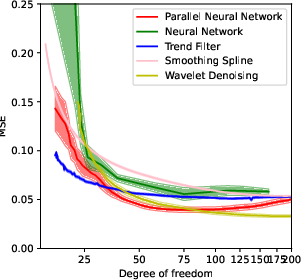
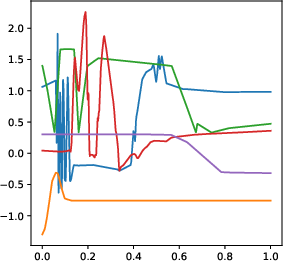
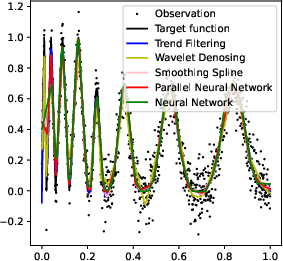
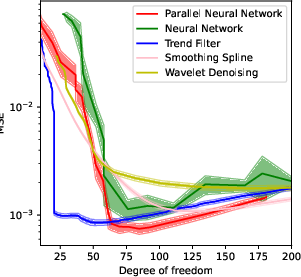
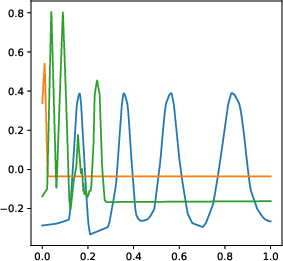
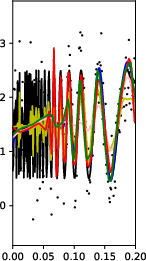
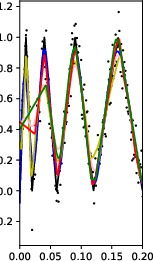
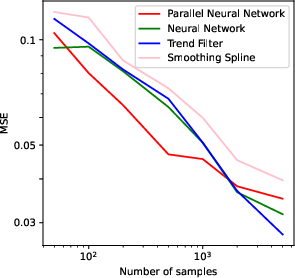
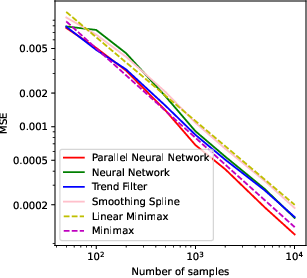
Figure 1: Numerical experiment results of the Doppler function (a-c,h), and vary'' function (d-f,g). All theactive'' subnetworks are plotted in (c)(f). The horizontal axis in (b) is not linear.

Regularization and Local Adaptivity

A central theme in the paper is the connection between weight decay and the sparsity of neural network representations. The paper shows that $\ell_2$ regularization in these networks corresponds to $\ell_p$-sparsity in the coefficient space of learned function bases, akin to a dictionary learning process. This insight provides a rigorous framework explaining the local adaptivity of neural networks, illustrating their advantage over kernel methods in efficiently learning functions with variable smoothness.

Theoretical Insights and Implications

One of the significant theoretical contributions is demonstrating that deeper networks can achieve closer approximations to optimal error rates. This property is particularly notable, as it provides a theoretical justification for the empirical observations that deeper neural networks typically outperform shallow networks in complex function approximation tasks. The implications of these findings are profound, offering a pathway to design networks that are naturally more adaptive to a wide range of functional characteristics without extensive architectural tuning.

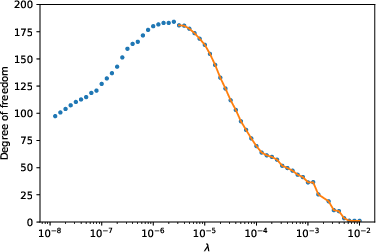
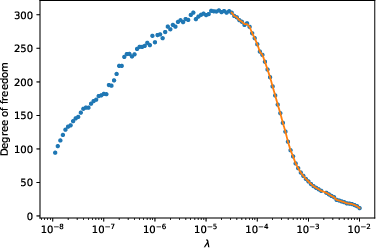
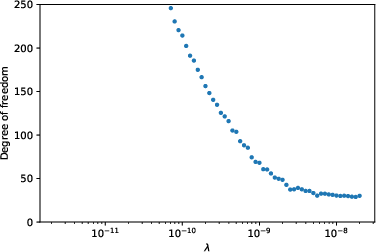
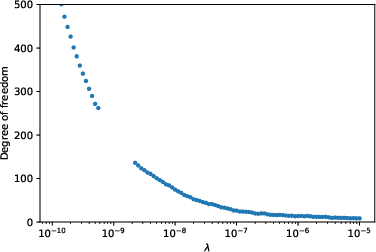
Figure 2: The relationship between degree of freedom and the scaling factor of the regularizer $\lambda$. The solid line shows the result after denoising. (a)(b) in a parallel NN. (c)(d) In trend filtering. (a)(c): the ``vary'' function. (b)(d) the doppler function.

Practical Experimentation

The paper provides an extensive set of numerical experiments that demonstrate the practical efficacy of the proposed parallel neural network model. These experiments validate the theoretical claims by showing that the model achieves comparable performance to classical nonparametric methods, such as wavelets and trend filtering, particularly in capturing local adaptivity in function estimation.

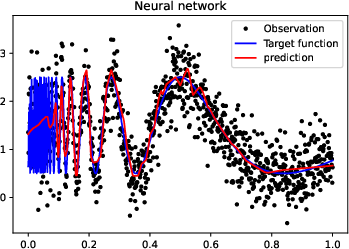
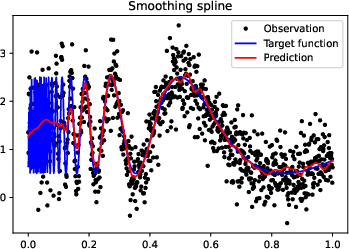
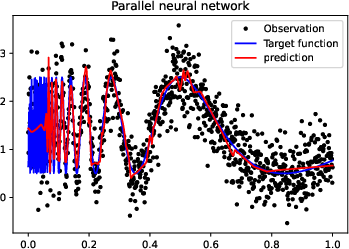
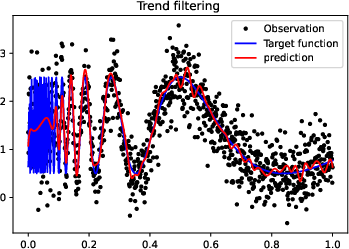
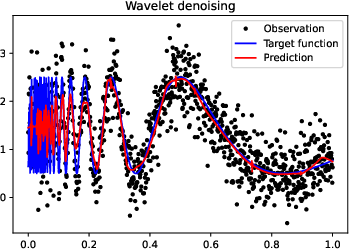
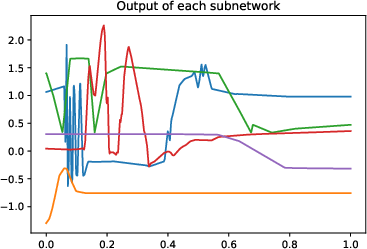
Figure 3: More experiments results of Doppler function.

Conclusion

The research presented in this paper highlights the promise of parallel neural networks with $\ell_2$ regularization for nonparametric regression tasks. By drawing connections between neural network architecture and traditional function space theory, the paper provides a solid foundation for further exploration into adaptive neural network designs. This approach could pave the way for more robust models capable of handling the diverse nature of real-world data, improving upon traditional kernel methods and situating neural networks as a decisive tool in statistical learning.

Future Directions

The implications of this paper encourage several future research directions. Extending this framework to more complex or higher-dimensional function spaces could further demonstrate the versatility of parallel neural networks. Additionally, integrating these concepts with recent advancements in neural architecture search or hyperparameter optimization might automate and enhance the design process, thus optimizing performance across various applications.

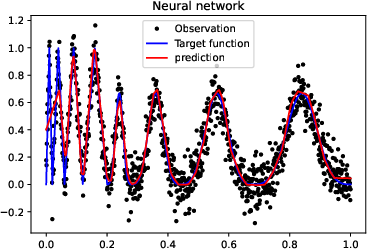
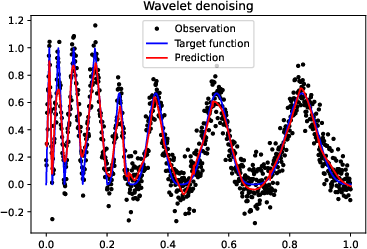
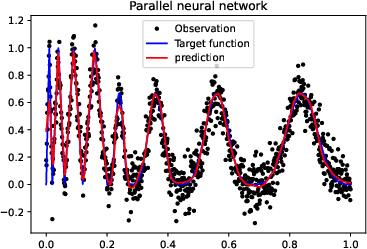
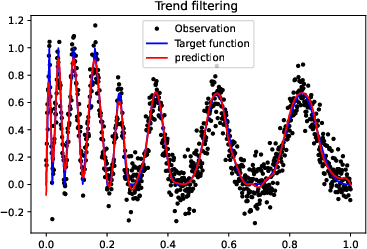
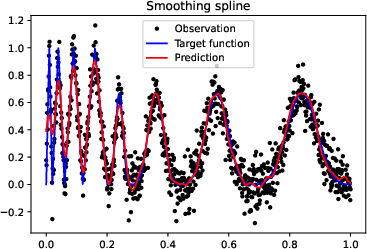
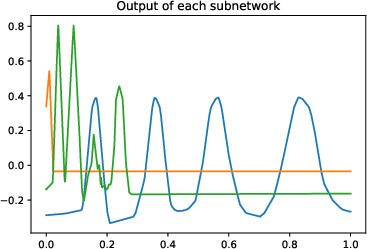
Figure 4: More experiments results of the ``vary'' function.