Bayesian Robust Tensor Ring Model for Incomplete Multiway Data (2202.13321v2)

Abstract: Robust tensor completion (RTC) aims to recover a low-rank tensor from its incomplete observation with outlier corruption. The recently proposed tensor ring (TR) model has demonstrated superiority in solving the RTC problem. However, the existing methods either require a pre-assigned TR rank or aggressively pursue the minimum TR rank, thereby often leading to biased solutions in the presence of noise. In this paper, a Bayesian robust tensor ring decomposition (BRTR) method is proposed to give more accurate solutions to the RTC problem, which can avoid exquisite selection of the TR rank and penalty parameters. A variational Bayesian (VB) algorithm is developed to infer the probability distribution of posteriors. During the learning process, BRTR can prune off slices of core tensor with marginal components, resulting in automatic TR rank detection. Extensive experiments show that BRTR can achieve significantly improved performance than other state-of-the-art methods.

• The paper introduces a Bayesian model that automatically determines tensor ring ranks and robustly recovers low-rank tensors from incomplete, noisy data.
• It leverages a variational Bayesian inference algorithm to iteratively refine latent core tensors and prune unnecessary components.
• Experimental results on color images, hyperspectral data, and videos show lower relative standard error and higher peak signal-to-noise ratio compared to state-of-the-art methods.

Bayesian Robust Tensor Ring Model for Incomplete Multiway Data

Introduction

The paper "Bayesian Robust Tensor Ring Decomposition for Incomplete Multiway Data" presents an advanced method aimed at solving the robust tensor completion (RTC) problem using a Bayesian framework (2202.13321). The primary goal is to recover low-rank tensors from incomplete datasets that may be corrupted by noise and outliers. This need arises from the fact that many real-world datasets are inherently tensor-shaped but often suffer from missing entries due to various reasons such as sensor malfunctions or occlusions.

A significant hallmark of the proposed method is the use of the Tensor Ring (TR) model. The existing TR approaches either require a predetermined TR rank or target the minimum TR rank aggressively, which can induce bias when noise is present. The authors introduce a Bayesian robust tensor ring (BRTR) approach to overcome these shortcomings through the automatic determination of TR rank and bias-free recovery from noisy data. This method is further reinforced by a variational Bayesian (VB) algorithm to precisely infer the posterior distributions.

Bayesian Robust Tensor Ring Decomposition

The BRTR model employs a probabilistic framework that inherently accounts for robust noise handling and automatic rank determination, which are incorporated into the model via Bayesian probabilistic reasoning. This approach not only estimates the low-rank tensor structure but also effectively separates out sparse noise components without requiring user-specified rank parameters.

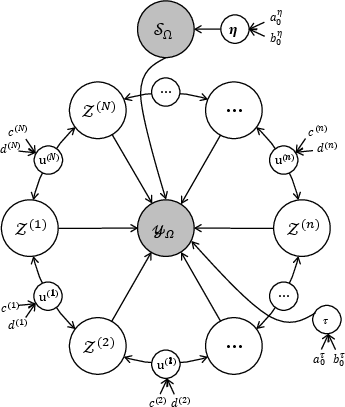
Figure 1: The graphical illustration of the BRTR model.

The tensor ring decomposition leverages a series of latent core tensors, allowing the representation of multiway data with flexibility in capturing its underlying structure. The BRTR model proceeds by using a VB algorithm to iteratively refine the posterior distributions of these core tensors while simultaneously pruning unnecessary components, leading to more accurate reconstructions of the original data.

Experimental Validation

The experimental section of the paper robustly validates the proposed BRTR method against several state-of-the-art techniques on both synthetic and real-world datasets including color images, hyperspectral data, facial images, and video sequences. Notably, the BRTR achieves superior performance in recovering data, demonstrating lower relative standard error (RSE) and higher peak signal-to-noise ratio (PSNR) than alternatives.

In the context of color images, the application of BRTR is shown to remarkably outperform other robust tensor completion methods. This is evidenced by figures illustrating recovery of color images from highly incomplete data with significant noise levels.

Figure 2: Testing color images.

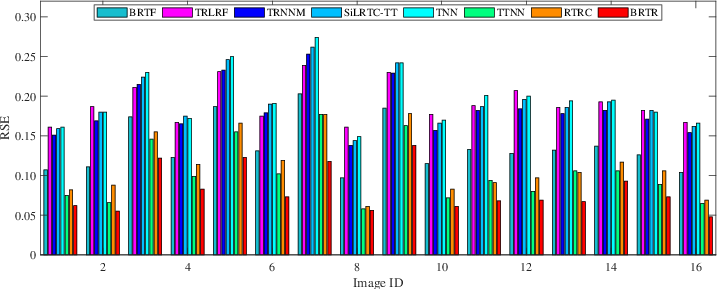
Figure 3: The RSE on testing color images with MR = 70% and SR = 10% over BRTF, TRLRF, TRNNM, SiLRTC-TT, TNN, TTNN, RTRC and BRTR methods.

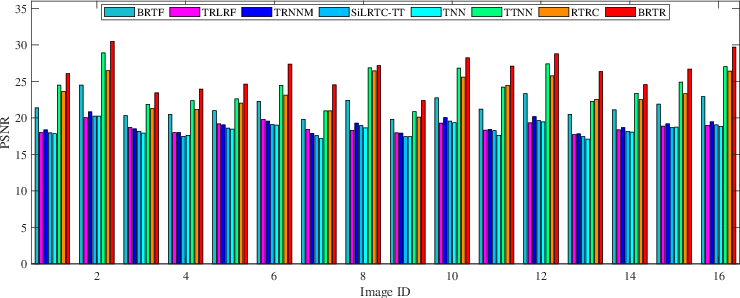
Figure 4: The PSNR on testing color images with MR = 70% and SR = 10% over BRTF, TRLRF, TRNNM, SiLRTC-TT, TNN, TTNN, RTRC and BRTR methods.

Implications and Future Work

The paper's contribution lies in demonstrating how BRTR can automatically and robustly adapt to complex data settings with minimal manual tuning. The automatic rank detection feature is particularly beneficial in practical applications where data dimensionality may be dynamically unknown or subject to change.

On the theoretical front, this approach opens new avenues for applying fully Bayesian methods to tensor decompositions beyond the typical constraints of fixed or manually-tuned parameters. The results strongly indicate that Bayesian methodologies can offer robust solutions to persistent data recovery challenges in the presence of noise.

While the BRTR model shows promising advancements, the computational overhead remains a challenge due to the iterative nature of the VB algorithm and high dimensionality of data involved in tensor ring decomposition. Future work could focus on optimizing the computational aspects, possibly by integrating distributed computing strategies or employing more efficient approximation techniques.

Conclusion

The BRTR model significantly advances the field of tensor completion by effectively handling incomplete and noisy multiway data. It surpasses existing methods by providing robust, statistically-grounded solutions that do not rely on predetermined parameters, thereby setting a new standard for performing tensor recovery tasks in complex conditions. As it stands, the BRTR approach is well-poised to benefit various fields such as image processing, remote sensing, and video surveillance, where incomplete data and noise are prevalent issues.